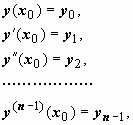Задачи коши для линейного оду 1 го порядка.

Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка, записанное в нормальной форме:

Областью определения уравнения называется область D определения правой части уравненияf(x, y), D ⊂ R² .

Функция y = y(x) является решением задачи Коши  

если y = y(x) дифференцируема на [a, b] , (x, y(x)) ∈ D   для всех x из [a, b] ,   y(x₀) = y₀ , x₀∈[a,b], и при подстановке в уравнение обращает его в тождество:

Фундаментальным результатом теории обыкновенных дифференциальных уравнений являетсятеорема существования и единственности решения задачи Коши:

Пусть функция f(x, y) и ее частная производная   f_y(x, y)  непрерывны в некоторой области Dплоскости x0y и точка (x₀, y₀) принадлежит области D.

Тогда :

— в некоторой окрестности (x₀ − δ, x₀ + δ) точки x₀ существует решение задачи Коши  

— если y = φ₁(x) и y = φ₂(x) два решения задачи Коши, то φ₁(x) = φ₂(x) на (x₀ − δ, x₀ + δ) .

Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x₀,y₀) области D проходит единственная интегральная кривая уравнения.

Бесконечное множество решений уравнения  

можно рассматривать как однопараметрическое семейство функций y = φ(x; x₀) — семействорешений задачи Коши  

элементы которого различны для разных значений x₀ . Иными словами область D"расслаивается" на интегральные кривые y = φ(x; x₀) . 

Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀ . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.

ОДУ 2 порядка, правая часть которого не содержит явного[x]

Опр. Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов): .  Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).  Опр. Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.  Опр. Общим решением (общим интегралом) уравнения называется такое соотношение  , что:  1. Любое решение   этого соотношения относительно y (для набора постоянных C₁, C₂, …, C_n из некоторой областиn-мерного пространства) является частным решением уравнения ;  2. Любое частное решение уравнения может быть получено из общего решения   при некотором наборе постоянных C₁, C₂, …, C_n.  Основную теорему - теорему о существовании и единственности решения задачи Коши для уравнения n-го порядка -мы сформулируем для записи уравнения в форме, разрешённой относительно старшей производной:  .  14.4.1. Постановка задачи Коши для уравнения n-го порядка: требуется найти решение уравнения

;

(17)

удовлетворяющее начальным условиям

(18)

где y₀, y₁, y₂, …, y_n-1 - заданные числа.  В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x₀, y₀,) с заданным угловым коэффициентом y₁.

Теорема существования и единственности решения задачи Коши: Пусть функция f(x, y, p₁, p₂, …, p_n-1) непрерывна и имеет непрерывные частные производные   в некоторой области D n + 1-мерного евклидового пространства переменных(x, y, p₁, p₂, …, p_n-1), и пусть точка (x₀, y₀, y₁, y₂, …, y_n-1) принадлежит области D. Тогда в некоторой окрестности точки x₀ существует решение уравнения (17), удовлетворяющее начальным условиям (18). Это решение единственно.

14.4.2. Некоторые типы уравнений, допускающие понижение порядка.  14.4.2.1. Уравнение вида   решается последовательным n-кратным интегрированием. Пример: 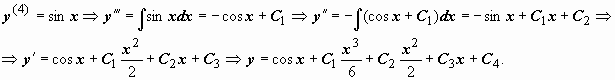   Переобозначив постояные, общее решение запишем в виде y = cos x + C₁x³ + C₂x² + C₃x + C₄.  14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения видаF(x, y^(k), y^(k+1), y^(k+2), …,y⁽ⁿ⁾) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y^(k)(x). Тогда   z^(n-k) = y⁽ⁿ⁾(x), и относительно z(x) уравнение примет вид  , т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y^(k) = z(x).  Пример: решить задачу Коши:  .  Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции  . Тогда  , и уравнение примет вид  . 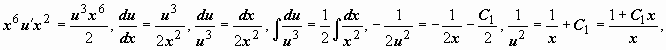Это - уравнение Бернулли; пусть z = uv, тогда  ,  ,  ,   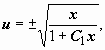  следовательно,  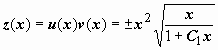. Относительно y(x) - это уравнение 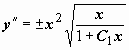 . Мы можем последовательно находить 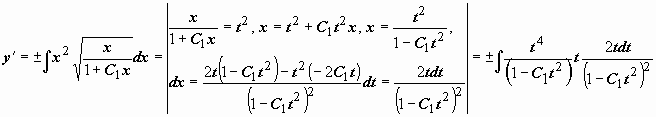  и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия   при x = 1 можно определить и знак частного решения, и значение постояннойC₁: 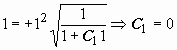 . Теперь 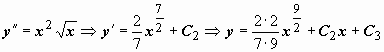 . Из условия   при x = 1 находим C₂: 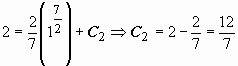 ; из условия y = 3 при x = 1 находим C₃: 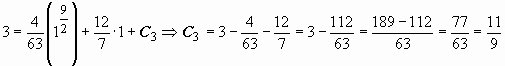 . Окончательный ответ:  .  14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения  , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость   от y:  . Старшие производные y по x вычисляются по правилу дифференцирования сложной функции:  .

Аналогично, 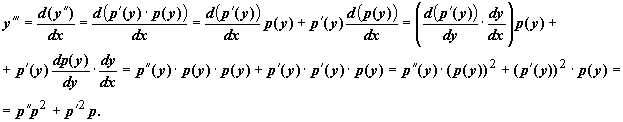   Также находятся следующие производные, и всегда k -ая производная y по x выражается через k-1 -ую производную p по y. В случае уравнения второго порядка   в результате таких преобразований получим  , т.е. уравнение первого порядка (в котором yвыступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C₁) этого уравнения решается уравнение  , решение которого y = y(x, C₁, C₂) будет общим решением исходного уравнения.  Примеры: 1. Задача Коши  .  Переменная x явно в уравнение не входит, поэтому полагаем  ,  , тогда  . Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений  , поэтому рассматриваем два случая:  1.  ; 2.  Это - уравнение с разделяющимися переменными:  . Получено уравнение  , решаем его:    . Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C₂ = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из  . Далее, из   следует, что  , т.е. C₂ = 0. Частное решение -  , т.е. y = 2.  Пример 2.    Решение:  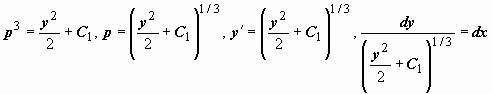  . Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть  , то получим 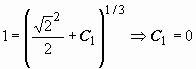 . Поэтому частное решение должно удовлетворять уравнению 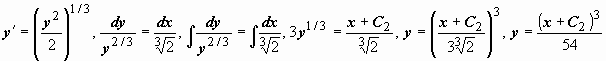 . Находим  :  . Ответ: решение задачи Коши 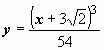 .