3.2. Феноменология проективности. Проективно-геометрическая структура как условие пространственности линейного образа
Мы должны рассмотреть ровность в линейном образе как сочетании линий. Рассмотрение ровности в сочетании линий, т. е. установление условий этой ровности, есть установление собственной пространственной феноменальности линейного образа, т. е. описание условия его собственного пространственного существования.
Линейное сочетание – это пересечение линий. Линии сочетаются тогда, когда они пересекаются. Ровность в пересечении линий – это некий атрибут, присутствующий в пересечении линий. Таким атрибутом пересечения линий, играющим роль механизма, «вырабатывающего» ровность в линейном сочетании, является угол.
Угол – это нечто, всегда присутствующее в пересечении линий. Угол – это некий соизмеритель линий, сочетающихся в пересечении линий. Угол – это нечто, задающее одну и ту же размерность как некую меру в соотношении пересекающихся линий независимо от удаленности от вершины, т. е. при непрерывно преобразующемся расстоянии между сторонами угла.
Размерность в соотношении пересекающихся линий не определяется расстоянием между ними, т. е. тем, что может быть внешне конгруэнтно чему-то. Размерность в пересекающихся линиях дана непосредственно и внутри их сочетания, независимо от какой-либо конгруэнции с каким-либо расстоянием. Она именно дана как непосредственно сопровождающий сочетание линий внутренний в нем атрибут их пересечения, как то, посредством чего не извне, но изнутри себя самого сочетание линий открывается как таковое – как феномен сочетания. Это означает: то, что мы называем углом, есть некая феноменально данная устойчивость в соотношении пересекающихся линий, выступающая условием эквивалентности (симметричности) преобразующихся и внешне неэквивалентных расстояний между сторонами. То есть угол – это феномен динамической симметрии в сочетании линий.
Угол есть специфический феномен, который динамически-симметрически соотносит именно линии. Можно сказать, что угол – это линейно выраженная динамическая симметрия. Невозможен угол в чем-либо, кроме сочетания линий. Это феноменально данный динамически-симметрический номинал именно в сочетании линий. Иными словами, угол – это специфически линейный феномен, динамически-симметрический номинал линейности.
Подобно тому, как линия есть номинально и в этом смысле неуловимо (неясно, но не неотчетливо) существующий между кривизной и прямизной феномен, данный в окружности либо в прямой как ровность в них, так и угол есть неясный, смутно-отчетливый и в этом смысле номинальный феномен пространственности, данный в самой линейности, в сочетании линий.
Угол – это элемент геометрического дискурса, образ-номинал, форма, открыто наблюдаемая в опыте или данная ментально, возникающая именно как динамически-симметрический номинал структуры линейности, т. е. в соотношении линий. Пожалуй, здесь действительно кроется «существование физических стимулов (например световых волн) – так, как будто они не просто раскрываются на основе опыта, но, в некотором смысле, даны нам»1. Иными словами, антисимметрия, коренящаяся в световой природе пространства и закрытая для восприятия в собственном квантово-бинарном пространстве, вновь, как в случае с линией, непосредственно открывается в виде угла как динамически-симметрической геометрической образности.
Итак, ровность как свойство линейного сочетания есть свойство угла в этом сочетании.
Ровность как свойство угла это конгруэнция его сторон. Конгруэнция – это совмещение соотносимых элементов. Таким образом, ровность в линейном сочетании есть совмещение линий в нем как сторон угла. Вопрос о конгруэнции – это вопрос об основаниях определения расстояния, поскольку определение расстояния – это совмещение его с другим, встроенным в некоторую систему измерения расстоянием. Определение расстояния, обусловленное совмещением его с другим, есть измерение, что есть суть геометрии, поскольку геометрия – это измерение расстояния1. Таким образом, вопрос о ровности угла – вопрос геометрический.
Итак, ровность в сочетании линий существует тогда, когда происходит совмещение линий как сторон угла.
Совмещение – это отсутствие расстояния. Отсутствие расстояния между линиями-сторонами угла это равность между этими линиями, обусловленная равенством расстояния между ними. Мы находим такую возможную в текущем контексте разницу между значениями слов «равность» и «равенство». Равенство – это симметрическое отношение расстояний, сопряженное, например, с числовым синтаксисом через опосредующие, задающие масштаб объекты. Равность – это симметрическое отношение самих тех линий, расстояния между которыми обладают равенством в том его частном и особом случае, когда это равенство свободно от опосредующих объектов (например других линий) и числового синтаксиса. Отсутствие расстояния между линиями есть свободное от численно-масштабного опосредования равенство расстояния между ними, порождающее равность их. Мы видим эту равность, когда совмещаем две линии: при этом видим именно пару линий (не «2» линии) на «отсутствующем» расстоянии – пару равных линий, а не одну линию. Мы находим дифференциальное различие между этими равными линиями. Это происходит только тогда, когда нам дано равенство расстояния между ними, которое не обусловлено ничем внешним и промежуточным и которое мы можем назвать в числовом синтаксисе «нулевым», или (говоря без привязки к числовому синтаксису) минимальным. Без минимального расстояния конгруэнция линий не конституируется – получается просто одна линия.
Итак, отсутствие расстояния – это равность как равенство минимального расстояния. Таким образом, ровность угла обоснована равностью как равенством минимального расстояния между его сторонами (равенство минимального расстояния можно рассматривать в любом расстоянии между линиями как остаток за вычетом измеряемого (доступного в измерении) расстояния).
Равенство минимального расстояния между сторонами угла можно рассмотреть как параллельность этих линий. Параллельность и равенство являются взаимопереходными, флуктуирующими друг в друга номинальными образами, указывающими друг в друга, а на самом деле на один и тот же общий для них феномен друг в друге, – равность. Поэтому, если мы укажем и опишем условия параллельности сторон угла, то тем самым найдем условия равности минимального расстояния между сторонами угла, т. е. условие равности их как линий, и в итоге – условие ровности угла.
Мы должны найти и затем описать, т. е. феноменологически определить условия того, как стороны угла в линейном сочетании являются параллельными. В этих условиях равность его сторон как условие конгруэнции и ровности. Таким образом, в рамках вопроса о ровности, конгруэнции и равности возникает и становится необходимым в качестве отдельного вопрос о параллельности. Параллельность – это феномен, который открывает равность и обуславливает в линейном сочетании ровность.
Итак, как параллельность может быть в углу? Возможны ли условия, при которых параллельность присутствует в углу и обусловлена углом, т. е. собственно той сущностью, что образуется сочетанием линий?
Эти условия можно описать, исходя из основ проективной геометрии.
Проективная геометрия описывает проективное пространство. «Проективное пространство можно получить, пополняя евклидово пространство бесконечно удаленными точками, которые образуют бесконечно удаленную плоскость: каждая другая плоскость пересекает ее по своей бесконечно удаленной прямой. Параллельные плоскости пересекаются по бесконечно удаленной прямой – она у них общая. Так же параллельные прямые пересекаются в их общей бесконечно удаленной точке»1. «Пространство, пополненное таким образом бесконечно удаленной плоскостью, становится проективным пространством, когда бесконечно удаленные его элементы – точки, прямые, плоскость – полагаются «равноправными» с соответствующими обычными его элементами. Точно это можно определить с помощью проективных преобразований»2. «Проективным пространством называется пространство, пополненное бесконечно удаленными элементами, если в нем введены проективные преобразования»3. Проективное пространство – это пространство, в котором возможны проективные преобразования. «Проективными преобразованием пополненного пространства называется такое его взаимно однозначное отображение на себя, при котором прямые отображаются на прямые, плоскости – на плоскости, без различия между обычными и бесконечно удаленными. Благодаря таким преобразованиям пополненное пространство и становится проективным»4. Иными словами, проективное преобразование – это автоморфизм проективного пространства, при котором устанавливается равноправие между «обычными» и «бесконечно удаленными» элементами. «Для определения проективных преобразований на плоскости следует дополнить плоскость бесконечно удаленными точками, считая, что все прямые, параллельные друг другу, обладают единственной бесконечно удаленной точкой»5. То есть проективное пространство определяется представлением «бесконечно удаленных точек» и связанным с ним представлением о пересечении параллельных прямых. В проективном пространстве параллельные прямые «имеют общую бесконечно удаленную точку», т. е. они пересекаются.
Можно сказать, что «бесконечность» удаленности точки пересечения параллельных линий в проективной геометрии означает «бесконечность» (как неопределимость, «безопределимость» и неизмеримость) минимальности угла между ними. Таким образом, параллельность пересекающихся линий не есть противоречие и семантический нонсенс, но означает, что минимальный угол здесь есть некоторый неопределимо, «бесконечно» минимальный угол, но не есть нулевой угол. Иными словами: можно сказать, что в проективной геометрии минимальный угол не есть нулевой.
Заметим, что возникновение проективной геометрии есть первый шаг в истории геометрии, приближающий эту науку к осознанию и описанию (опознанию) структуры несовместимых пространств: несовместимых как несоизмеримых в численном синтаксисе и несовместимых как опосредованно номинальностью бинарных в собственно образно-номинальном дискурсе.
Итак, в проективном пространстве параллельные линии (т. е. все линии) пересекаются. Возникает вопрос: как возможно равенство между параллельными линиями в проективном пространстве? Это вопрос феноменологический, ибо он означает постановку следующего вопроса: как понять и описать сам феномен параллельности в проективном пространстве? То, как возможна параллельность в проективном пространстве, поможет нам понять, как возможна параллельность в углу.
Какие-либо преобразования предусматривают условия инвариантности в них. Преобразование предполагает инвариантность, в соответствии с которой происходит соизмерение каких-либо явлений, подлежащих этим преобразованиям. То есть инвариантность в преобразованиях – это условие соизмеримости, т. е. условие равенства, т. е. численного и номинально-образного (дискурсивного) соотношения константы измерения и измеряемого явления. Всякая геометрия – это структура инвариантности преобразований, описываемых этой геометрией. «Проективная геометрия – раздел геометрии, изучающий свойства фигур, не меняющихся при проективных преобразованиях»1. То есть проективная геометрия, как структура измерения проективного пространства, задает условие инвариантности при проективных преобразованиях. Этим условием является коллинеарность.
Коллинеарность – это принадлежность каких-либо явлений некоторой общей для них линии. Чаще всего коллинеарностью обозначается принадлежность минимум трех точек некоторой прямой линии. В этом случае указание на коллинеарность этих точек имеет значение того обстоятельства, что данные точки совпадают с линией. Также можно усмотреть здесь совпадение трех линий, соединяющих каждую из трех пар точек в этих трех точках, друг с другом и с данной линией. Для менее чем трех точек это особое обстоятельство не усматривается на том основании, что в прохождении линии через две точки никакого совпадения нет, поскольку нет разных пар точек и разных линий, которые могли бы различаться и затем совпадать друг с другом.
Коллинеарность как инвариантность при проективных преобразованиях, т. е. как условие равенства, означает, что все, что находится на одной линии, сохраняется при проективных преобразованиях находящимся на одной линии. То есть равенство происходит тогда, когда некие элементы («точки»), находящиеся на линии, совмещаются с другими элементами, находящимися на другой линии, посредством пересечения в них этих линий поперечными линиями, проходящими через соответствующие друг другу элементы (рис. 1).
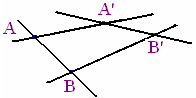
Рис. 1
Равенство здесь это равенство отрезков АВ и А'В'. Это равенство означает, что отношение между элементами А и В, находящимися на одной линии, в номинальном и возможном численном выражении соответствует отношению между А' и В', тоже находящимися на одной линии. То есть какому-либо возможному элементу Χ на коллинеарности АВ (рис. 2) соответствует элемент Χ', находящийся на коллинеарности А'В'. То есть нет на коллинеарности АВ элемента, которому не было бы соответствующего ему элемента на А'В'.
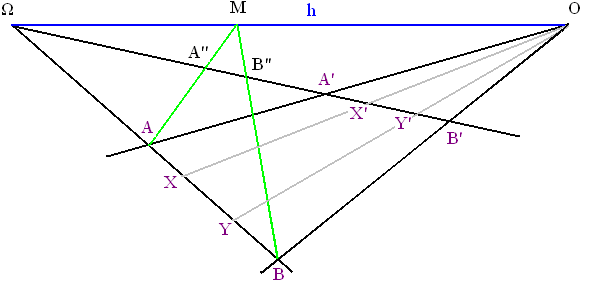
Рис. 2
Таким образом, то, что АВ как совокупность коллинеарных элементов (номинальная или численная) равна А'В' как коллинеарной совокупности, означает, что АВ и А'В' совпадают во всей их длине, по каждому номинально или множественно определяемому элементу – т. е. они совмещаются, образуют конгруэнцию, и вследствие этого они равны.
Конгруэнция и равенство коллинеарностей всегда обусловлены парой линий, проходящих через соответствующие друг другу элементы, ограничивающие некие соизмеряемые отрезки. Равенство коллинеарностей обеспечивается пересечением пары линий, на которых находятся сравниваемые коллинеарности, другой парой линий, соединяющих эти коллинеарности. То есть равенство коллинеарностей обеспечивается парностью двух пар линий.
Парность в соотношении этих двух пар линий является инвариантной структурой равенства коллинеарностей. То есть всякое равное соотношение двух коллинеарностей обеспечивается тем, что оно происходит в паре с пересекающими их двумя «поперечными» линиями – именно через пересечение этих «поперечных» линий друг с другом. В этом пересечении (в точке Ο на рис. 2) соотносимые коллинеарности совмещаются друг с другом в мере их минимального различия, достигая его по отдельности в том пределе, в направлении которого каждая из коллинеарностей соотносится с другой. Иными словами, коллинеарности АВ и А'В' (см. рис. 2) соотносятся друг с другом не непосредственно, но посредством пересечения О, только в котором, как в собственном пределе для каждой из них, и через которое они совмещаются и обретают равенство, в котором они интегрально сводятся и определяются («определиваются») как равные. То есть, если представить равенство АВ и А'В' как проецирующий путь по линиям АА' и ВВ' в векторном выражении, то это будет выглядеть не как АА' и ВВ', но как АОА' и ВОВ'. Таким образом, равенство АВ и А'В' это не АВ = А'В', но АВ = О = А'В'.
Пересечение О – это, можно сказать, номинальный узел, через который и соотносясь с которым какая-либо отдельная линия XX' (т. е. соотносясь на самом деле с парой линий АА'/ ВВ', точнее, с одной из линий этой пары) обозначает соответствующий элементу Х элемент Х'. Иными словами, любая «внутренняя» линия, совмещающая некий элемент X, принадлежащий АВ, с элементом X', принадлежащим А'В', парно совмещается с узлом О, т. е. с парой линий АА'/ВВ'. Поэтому линии XX' и ΥΥ', соединяющие («перебрасывающие») внутри равенства АВ и А'В' элемент Х в Х' и элемент Y в Y', являются парными (каждая из них в отдельности) по отношению пересечению линий АА'/ВВ', пересекающими их в их пересечении и, соответственно, пересекающимися друг с другом в нем же, образуя так называемый «пучок линий» в точке О.
Когда коллинеарности АВ и А'В' интегрируются в узле О, они феноменально поворачиваются. Имеется в виду то, что в движении к узлу О линии АВ и А'В' поворачиваются вокруг центра Ω. Именно поэтому они становятся смыкающимися: они совмещаются на линии ΩΟ. Находясь в узле О, представляясь там в «сжатом» виде и совмещаясь там друг с другом, интегрированные коллинеарности АВ и А'B' не исчезают, не превращаются в «точку», но выстраиваются на линии ΟΩ. Здесь, на линии ΟΩ каждая из интегрированных в узле О коллинеарностей становится коллинеарной с ней. Таким образом, то, в какой мере коллинеарности АВ и А'В' интегрируются в узле О в паре с линиями АА' и ВВ' и устанавливаются на линии ΟΩ, обретая именно на ней минимальное различие между собой как коллинеарность с ней и как равенство минимального расстояния между собой, равно тому, как парные для них линии АА' и ВВ' уже сами интегрируются в узле Ω и сжимаются до совпадения друг с другом на линии ΩΟ.
Таким образом, линия ΩΟ являет собой общий компонент в парности (АВ/А'В') / (АА'/ВВ'). Этот компонент является динамической константой сотношения коллинеарностей АВ/А'В': можно сказать, что в линии ΩΟ узел О, интегрирующий АВ и А'В', становится подвижным и обретает динамический характер. Именно в своей динамичности, т. е. в качестве линии ΟΩ, узел О связывает каждый элемент АВ не только с соответствующим элементом коллинеарности А'В', но и с каким-либо элементом всей линии А'В' – т. е. А'В', интегрированной в Ω или ΩВ'. То есть существует на линии ΩB' (например на отрезке ΩА') коллинеарность А''В'', которая равна АВ, если ее соотношение с АВ парно с динамическим узлом О, в данном случае имеющим место в «точке» М на линии ΟΩ. Иначе говоря, какая-либо пара линий, исходящих от точек А и В и пересекающихся на линии ΟΩ, отсекает на линии А'В' отрезок, равный АВ.
Таким образом, равенство коллинеарностей в пересекающихся парах линий АА'/ВВ' и АВ/А'В' образует (посредством своего динамического узла как внутренней константы этих пар линий) множество равенств коллинеарностей. В этих равенствах все пары линий, пересекающие линии АВ и А'В' (парные к ним), в пересечениях собственных линий коллинеарны друг с другом и совпадают с линией ΟΩ.
Таким образом, равенство коллинеарностей в паре двух пар пересекающихся линий АА'/ВВ' и АВ/А'В' необходимо и изнутри себя образует коллинеацию на линии ΟΩ. То есть множество пересечений линий во множестве равенств коллинеарностей, образуемых парами и АВ/А'В', само формирует линию ΟΩ, коллинеарно образует ее «из ничего». Эту коллинеарность, совпадающую с ΟΩ (точнее, включающую ΟΩ), назовем коллинеарностью h, или линией h.
Убедиться в том, что линия h образуется (может быть образована) как коллинеарность пересечений пар линий, каждая (пара) из которых исходит из АВ, последовательно и определенным образом пересекаясь со следующей парой, можно также посредством следующего, основанного на известной в проективной геометрии конфигурации Р. Дезарга, опыта.
Соединим точки А с В' и В с А' (рис. 3). Через полученное пересечение W проведем линию WΩ. Через точку W' на пересечении WΩ с АА' проведем линию ВW'. Через точку V на пересечении ВW' с ΩВ' проведем линию AV. Через точку W'' на пересечении WΩ с AV проведем линию ВW''. Через точку V' на пересечении ВW'' с ΩВ' проведем линию АV'. Через точку W''' на пересечении WΩ с AV' проведем линию ВW'''. Через точку V'' на пересечении ВW''' с ΩВ' проведем линию АV'', и т. д. Полученные пересечения ВW/AV, BW'/AV', BW''/AV'' и все последующие коллинеарны в линии h.
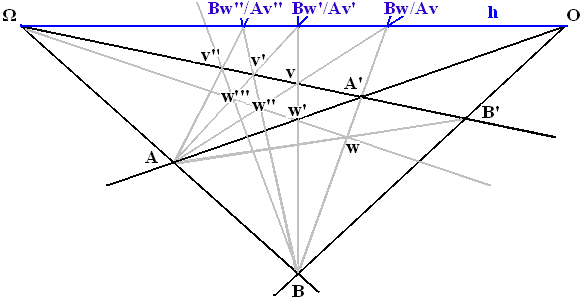
Рис. 3
Линия h выводится из равенства коллинеарностей в пересекающихся парах линий АА'/ВВ' и АВ/А'В' как его внутренне необходимый компонент, как внутренне необходимая его константа. Именно коллинеарное совпадение множества пересечений линий, образуемых равенством коллинеарностей в пересекающихся парах линий АА'/ВВ' и АВ/А'В', обуславливает в конечном итоге это равенство.
Это совпадение феноменально. Оно есть внутренний корень самой коллинеарности как условия равности в пространстве пересекающихся линий, т. е. в проективном пространстве, как необходимо и феноменально ими образуемое и непосредственно эксплицируемое совпадение. Оно есть внутреннее основание самой линейности как сочетания пересекающихся линий, феноменально ее повторяющее и утверждающее: показывающее в самой линейности как в сочетании пересекающихся линий ее саму как коллинеарность и обуславливающее ее тем самым как сущность – т. е. обуславливающее ее онтологически.
Линия h, как онтологически обуславливающее коллинеарность совпадение, конституирует коллинеарность не только как условие равенства, не только как условие инвариантности в проективных преобразованиях, но как тезис: через какие-либо две точки проходит линия. Линия h, проходящая через точки Ο и Ω, обуславливает собой какую-либо из линий, которые в представленной линейной схеме проходят через две точки. Иными словами, если между точками Ο и Ω существует коллинеарность, конституирующая линию, проходящую через Ο и Ω, то подобно этому и между любыми двумя точками (А и А', В и В', X и X' и т. д.) действительно проходит линия, т. к. любая такая пара точек суть интегрирующие узлы для каких-то других точек в связывающих их линиях.
Таким образом, коллинеарность есть онтологический тезис. Когда согласно тезису коллинеарности утверждается, что через две точки можно провести линию, тем самым утверждается, что линия там уже существует. «Проведение» линии есть лишь подчеркивание уже существующей до этого линии. Тезис коллинеарности есть не «проведение линии» – он не проводит линию, но есть именно предшествующий этому проведению постулат существования линии – онтологический постулат.
Представленная линейная схема показывает, как в сочетании пересекающихся линий, т. е. в проективном пространстве, образуется равенство: оно образуется посредством коллинеарности, которая феноменально продуцируется, возникает в этой схеме. Эта схема есть общий принцип инвариантности в проективном пространстве как образуемой в нем коллинеарности.
Эта схема является общим признаком (т. е. сущностью) так называемых проективно-геометрических конфигураций. Проективно-геомет-рические конфигурации – это линейные конструкции, имеющие аксиоматическое значение в проективной геометрии, простейшими и главными из которых являются конфигурации Паппа и Дезарга1. Будем называть рассматриваемую общую схему проективно-геометрических конфигураций проективно-геометрической структурой.
Проективно-геометрическая структура есть феноменально выраженное утверждение того, как именно сочетание пересекающихся линий порождает коллинеарность. Таким образом, получается, что коллинеарность в проективно-геометрической структуре (и в какой-либо проективно-геометрической конфигурации) внутренне взаимосвязана с положением о пересечении линий, т. е. с положением о пересечении параллельных, исходным в проективной геометрии. Проективно-геометрическая структура объединяет пересечение линий и коллинеарность. При этом положение о пересечении и положение о коллинеарности образуют некое двойственное единство – так называемую двойственность проективной геометрии. Двойственность здесь заключается в том, что подобно тому, как две точки связаны одной линией, две линии связаны одной точкой. То есть двойственным является само соотношение точки и линии в проективной геометрии. Тем самым тезис коллинеарности как утверждение того, что через две точки всегда проходит линия (т. е. что линия есть пересечение двух точек), означает в двойственном своем соответствии, что точка всегда есть пересечение двух линий. Таким образом, в проективно-геометрической структуре тезис коллинеарности внутренне и необходимо связан с тезисом пересечения: проективно-геометрическая структура делает пересекающиеся линии образующими коллинеарность, вследствие этого – коллинеарными, вследствие этого – равными.
Но проективно-геометрическая структура как структура инвариантности проективной геометрии внутренне не полна, или не самодостаточна, т. к. обусловлена обстоятельством, не предусматриваемом ни тезисом коллинеарности, ни тезисом пересечения. Этим обстоятельством является прохождение линии через некоторую «точку» пересечения двух других линий – т. е. пересечение трех линий в одной «точке». Это обстоятельство есть такое же совпадение «в точке», которое в двойственности проективной геометрии соответствует тому, как (согласно тезису коллинеарности) осуществляется совпадение точек «в линии», когда, например, три точки совпадают на линии. Этим обстоятельством как бы обеспечивается полнота двойственности проективной геометрии – полнота дуального соответствия тезиса пересечения тезису коллинеарности внутри проективно-геометрической конфигурации. Но это обстоятельство, будучи «используемым» проективно-геометрической структурой, не обусловлено ею, не содержится в ней. Тезис пересечения, который вместе с тезисом коллинеарности образует проективно-геометрическую структуру, если смотреть на него феноменологически аккуратно и внимательно, не содержит указанное обстоятельство.
Иными словами, тезис пересечения в том виде, в котором он используется в проективной геометрии, не «позволяет» провести через пересечение линий – через «точку» пересечения линий – третью линию. Говоря по-другому, в рамках тезиса пересечения попадание линии в пересечение (в «точку» пересечения) двух других линий является проблематичным. Эта третья линия неизбежно проваливается в некую сторону, что происходит потому, что феноменологически проблематично само пересечение двух линий, представляемое «точкой». Это пересечение в «точке» (если двигаться к нему в представлении о нем подобно тому, как линия, проходящая через точку пересечения двух других, движется к ней, пытаясь попасть в нее) непредставимо и немыслимо. Оно скрыто завесой дурной бесконечности «ахиллесовой черепахи». Поэтому немыслима сама «точка» в пересечении линий как совершенно мистический, оскорбительный своей нечеткостью объект.
Требуется, чтобы само пересечение линий, сам тезис пересечения линий был феноменологически установлен, верифицирован и избавлен от «точечности» как от ложной и неоправданной метафизичности. Требуется провести феноменологическое исследование, верифицирующее пересечение линий как феномен. В результате такой верификации тезис пересечения будет избавлен от «точечности» и дополнен исходя из своего феноменального значения именно таким образом, что тезис о «тройном» пересечении линий, требуемый для полноты проективно-геометрической структуры, станет частью содержания самого тезиса о пересечении – станет обстоятельством, внутренне подразумеваемым им.
Итак, требуется показать присутствие в проективно-геометри-ческой структуре тезиса о пересечении линией «точки» пересечения двух других линий, т. е. тем самым дополнить уже имеющийся в проективной геометрии постулат о пересечении двух линий до полноты его действительно двойственного соответствия тезису коллинеарности. Для этого нужно произвести феноменологическое исследование – феноменологическую реинсталляцию, переустановку самого тезиса пересечения, в результате чего этот тезис дополнится тезисом о прохождении линии через «точку» пересечения двух других линий как имманентным ему.
Отметим роль этого дополняющего тезиса. Тезис о прохождении линии через «точку» пересечения двух других линий утверждает само наличие некой сущности в пересечении двух линий. Этот тезис утверждает существование и является тезисом онтологическим, открывающим в направлении утверждаемой им сущности ряд следующих вопросов: как вообще возможно пересечение линий? как они не проваливаются в собственной одномерности, не растворяют друг друга в бесконечно-одномерной «тонкости» каждой из них? как они образуют место, принадлежащее обеим линиям, т. е. место, имеющее сразу два направления? Попросту говоря: как они «вяжутся»?
Все эти вопросы фокусируются, сходятся в некотором едином для них вопросе: как возможен угол в пересечении линий как именно та сущность, что связывает линии в их пересечении неким неуловимо уходящим в глубь их пересечения образом? Это феноменологический вопрос. Собственно здесь, в этом вопросе, обнаруживается граница между геометрией как вообще наукой, как сопряженной с числовым синтаксисом и раскрываемой таким образом симметричностью – с одной стороны, и феноменологическим описанием как текстом, как синтаксисом, содержащим неповторение, задающим направление в симметрии и разбивающим ее на чистую бинарность, т. е. антисимметричностью, – с другой стороны. Это та граница, в которой и за которой симметричность начинает не двоиться, но отражаться, обнаруживая в себе новое качество – неделимость «на два», несопряженность с числом, становясь по ту сторону некоторого фокуса, в верхней исчезающей кромке кристального пламени которого стирается тончайшая ткань различия между различием и повторением, и где симметричность обнаруживает свой корень и становится собственно антисимметричностью.
И только прагматически обусловленная невнимательность может игнорировать ту степень глубины (сущей глубины), которая кроется в феномене пересечения линий, в феномене угла, как он раскрывается через аксиоматику проективной геометрии.
Итак, проективно-геометрическая структура как общая схема проективно-геометрических конфигураций является условием параллельности/равенства пересекающихся линий как сторон угла (равенства расстояний между ними), и в таковом качестве она требует дополнения тезисом о «тройном» пересечении линий. Этот тезис ставит под вопрос само пересечение линий вообще как таковое, саму содержащуюся в нем сущность угла. Примечательно и важно, что независимо от своей роли как условия равности сторон угла проективно-геометрическая структура, будучи неполной, требует в качестве своего феноменологического дополнения именно рассмотрения сущности угла. То есть полнота проективно-геометрической структуры в качестве условия равенства сторон угла (в качестве условия ровности сочетания линий и линейного образа) требует раскрытия сущности угла.
Вопрос о равенстве сторон угла приводит к проективно-геометрической двойственности, а эта двойственность коренится в двойственности самой сущности угла. Двойственность сущности угла есть нечто большее, чем зримо данная двойственность феномена угла, выражающаяся в наличии в нем двух сочетающихся линий и в невозможности определения расстояния между сторонами угла в одной линии – в непрерывности ускользания его в некую двойственность расстояния. Двойственность сущности угла – это сама двойственность линии и точки, открывающаяся в проективно-геометрической структуре. Эта двойственность есть на самом деле двойственность линии и угла, который как сущность, усматриваемая в пересечении двух линий, заменяет мистическую точку и тем самым обеспечивает полноту проективно-геометрической структуры. Двойственность угла – это двойственность самой сущности пересечения линий, в которой неким образом происходит взаимосвязь линии с линией. Эта сущность неразрывно связана с сущностью линии, и двойственность сущности пересечения линий коренится в двойственности линии как сущности пространственности – как не двойственной, но именно бинарной сущности. Линия как сущность пространственности имеет квантово обусловленную двойственность, которую мы называем бинарностью. Таким образом, сама возможность взаимосвязи линии с линией и угол как двойственная сущность этой взаимосвязи коренятся в квантово-бинарном характере линии как сущности пространственности.
Иными словами, двойственность угла коренится в квантовой бинарности линии. Эта бинарность открыта в линии как существование в ней – как одновременность и одноместность, как единомерность существования – прямизны и кривизны, «свернутости» и «развернутости» пространства. Именно эта бинарность – бинарность самой пространственности – содержит ключ к пониманию того, как в линейности, в линейном образе, в проективно-геометрической структуре – т. е. благодаря углу – порождается, т. е. субстанциально и без каких-либо предусловий возникает линия – т. е. собственная пространственность как ровность и глубина линейного образа.
Квантовая бинарность линии должна быть феноменологически переоткрыта и сопряжена с проективно-геометрической структурой. Этим сопряжением будет обеспечена полнота проективно-геометри-ческой структуры, полнота ее собственной двойственности.
Таким образом, феноменологическая реинсталляция тезиса пересечения, обеспечивающая полноту проективно-геометрической структуры, это феноменологическое рассмотрение действия квантовой сущности линии в рамках этой структуры. Это рассмотрение устанавливает, по сути, взаимосвязь проективности и квантовости.