Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный исследовательский томский политехнический университет

Институт – Энергетический

Направление – Электроэнергетика

Кафедра – Электроснабжение промышленных предприятий

«Интерполяция функций и динамика нелинейных систем»

^{Наименование лабораторной работы}

Отчет по лабораторной работе № 4

по курсу «Дополнительные главы математики»

^{Наименование учебной дисциплины}

Вариант №6

Выполнил студент гр. 5АМ24 ________ С.С. Блощинский

^{Подпись Дата И.О.Фамилия}

Проверил доцент______ _______ _________ А.С. Глазырин

^{должность Подпись Дата И.О.Фамилия}

Томск – 2012

Содержание

Цель работы

1. Интерполяция кривой намагничивания

1.1 Интерполяция полиномом Ньютона

1.2 Интерполяция полиномом Ньютона в программной среде MathCAD

2. Расчёт переходного и установившегося процессов в цепи

2.1 Метод Рунге-Кутта второго порядка с полным шагом

2.2 Расчёт переходного и установившегося процессов в цепи с применением метода Рунге-Кутта второго порядка с полным шагом в программной среде MathCAD

3. Анализ гармонического состава тока нелинейной цепи в установившемся режиме

3.1 Разложение в ряд в Фурье

3.2 Гармонический анализ тока в программной среде MathCAD

Вывод

Список литературы

Контрольный вопрос

Цель работы: Освоить математический аппарат, алгоритмы интерполяции функций, заданных экспериментально полученными узлами, методы и алгоритмы гармонического анализа токов в нелинейных системах.

1. Интерполяция кривой намагничивания

Катушка (рисунок 1) имеет магнитный сердечник с нелинейной основной кривой намагничивания H(B), где B – магнитная индукция, Тл, H – напряжённость магнитного поля, А·м. Кривая намагничивания задана экспериментально снятыми узлами и представлена в таблице 1.

Таблица 1 – Основная кривая намагничивания магнитопровода катушки

В, Тл	0,5	0,8	0,9	1,0	1,1	1,2	1,3	1,4	1,5
Н, А/м	210	360	460	560	760	1010	1390	2010	3010

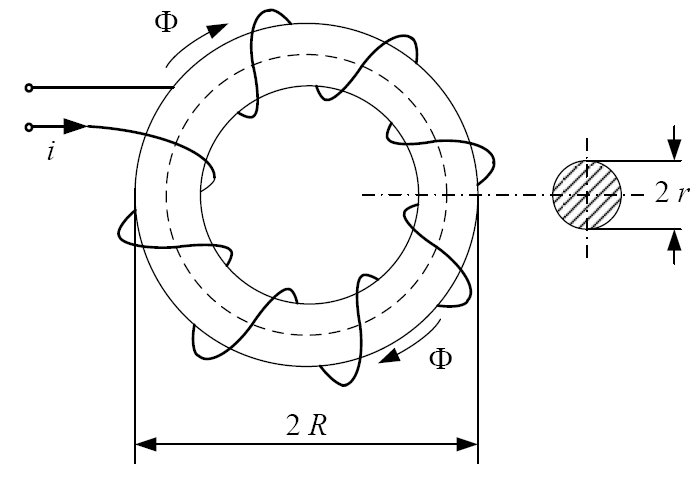
Рисунок 1 – Катушка с тороидальным магнитопроводом

Кривую намагничивания, заданную таблично следует подвергнуть интерполяции по методу Ньютона

1.1 Интерполяция полиномом Ньютона:

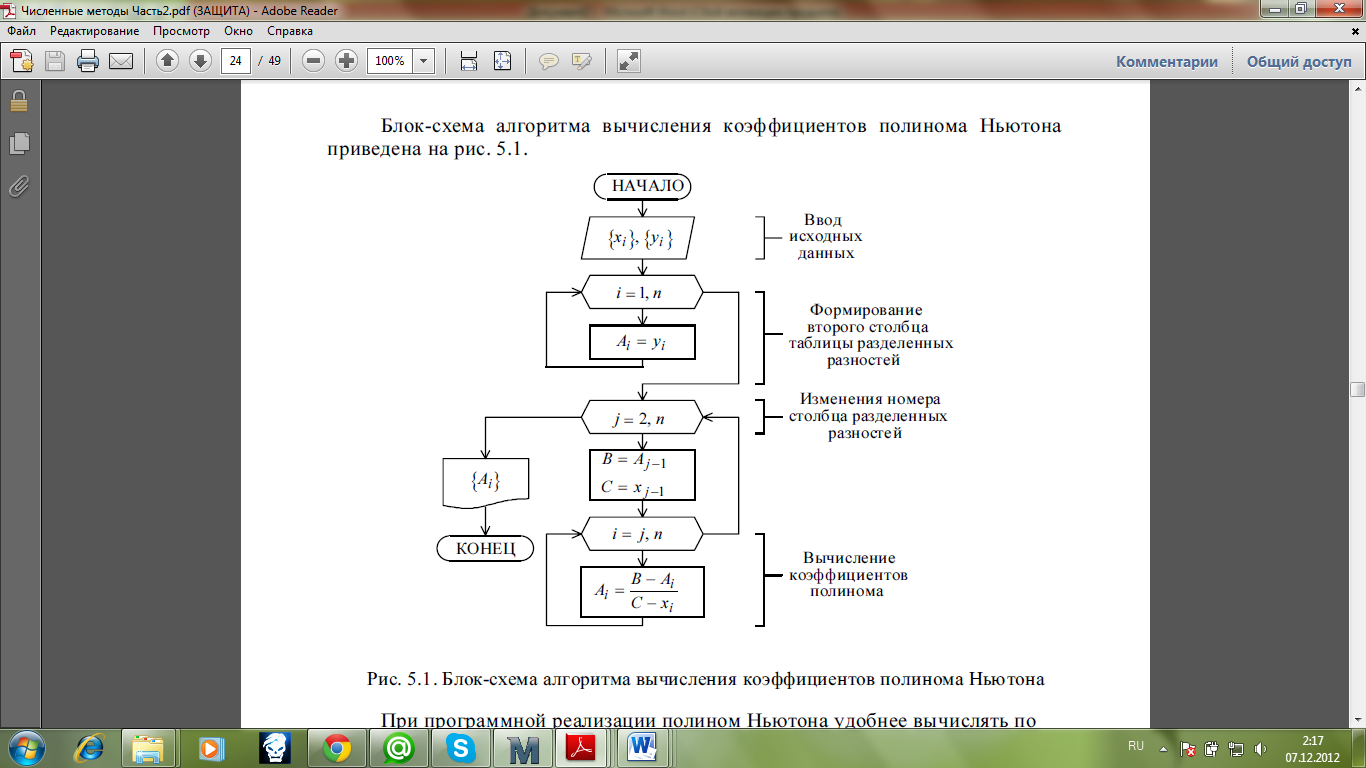
2. Расчёт переходного и установившегося процессов в цепи

В п. 1 после интерполирования получена зависимость H(B), позволяющая по текущему значению магнитной индукции B найти величину напряжённости магнитного поля H.

Зададимся геометрией катушки: l = 15·10^-2 м – средняя длина силовых линий напряжённости магнитного поля H в тороидальном магнитопроводе, S = 2·10^-4 м² – площадь поперечного сечения магнитопровода, w = 2000 – число витков катушки, R = 1 Ом.

Запишем дифференциальное уравнение (ДУ) равновесия электрической цепи

, (2.1)

где ψ – потокосцепление катушки.

Приведём ДУ (1) к нормальной форме Коши:

, (2.2)

Уравнение (2.2) можно решим методом Рунге-Кутта 2-го порядка с половинным шагом.

В процессе интегрирования ДУ (2.2) придётся на каждом шаге по известному значению потокосцепления катушки вычислять ток в катушке. Для того необходимо воспользоваться результатами интерполяции кривой H(B), выполненной в п.1, и известными соотношениями из теории магнитных цепей.

Магнитную индукцию B в магнитопроводе катушки можно выразить через S, w и ψ как

.

Ток в катушке можно рассчитать как

.