
Как извлечь корень из квадрата?
Пусть у нас есть хорошее число 2. Возведём его в квадрат.
22 = 4
Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:
Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:
![]()
Оно и естественно, правда? Возведение в квадрат компенсируется обратной операцией - извлечением квадратного корня. В общем виде формула выглядит вот так:
![]()
Стоп! Внимание! Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут: "где а - больше, либо равно нулю". В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Потому, что в примерах а частенько бывает отрицательным! Пока и мы будем считать, что а - неотрицательное. Для простоты. А вот как встретите на этой странице мрачного зайца - вот там и начнётся настоящая работа!
Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:
24=(22)2
Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь...
Теперь по формуле корня из квадрата:
![]()
Вот и всё. Корень из любой чётной степени даст в результате подкоренное выражение в степени, в два раза меньше исходной. Корень из 310 ? Легко! Это будет 35. Корень из 518 ? Запросто! Это будет 59. Ну, и так далее.
А если степень нечётная? Подумаешь! Раскладываем подкоренное выражение на множители - и вперёд! Используем вынесение множителя из-под корня. Например:
![]()
Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто... Вернём эту простоту и ясное понимание.
Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)
Итак, откуда в корнях могут появиться отрицательные числа и выражения?
Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:
Здесь всё понятно и просто.
А теперь попробуем вычислить:
![]()
Берём, и просто считаем, безо всяких формул:
(-2)2 = 4
Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) - всегда число неотрицательное! То есть:
![]()
А если бы мы использовали формулу:
получили бы не два, а минус два! Что является ошибкой.
Не работает эта формула для отрицательных значений.
Для того, чтобы формула корня из квадрата работала для всех значений а, она записывается вот так:
![]()
Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)
Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а,результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:
![]()
Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях.Например, требуется упростить выражение:
![]()
где х<0.
Казалось бы, ответ прост. Получится просто х. Но зачем тогда дополнительная информация?! Приходится соображать. Если х<0, это отрицательное число. Минус два, или минус тридцать, там... Но корень квадратный отрицательным быть не может! Это будет точно х, но он должен быть с плюсом! Где взять плюс? А мы его сделаем! Если перед заведомо отрицательным числом, поставить минус, это число станет, число станет положительным! И верное решение выглядит так.
![]()
Собственно, это и есть главная трудность в работе с корнями. В отличие от более простых разделов математики, здесь правильный ответ частенько не вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.)
И как справляться со всем разнообразием заданий с корнями? А есть ещё иррациональные уравнения и неравенства, где эти пунктики играют главную роль...
Главный практический совет по работе с квадратными корнями.
В любом задании с квадратными корнями лично контролируйте знаки подкоренного выражения и результата извлечения корня.
Прикидывайте, и оценивайте ситуацию, исходя из внешнего вида примера и всех дополнительных условий задания. Если под знаком корня - минус, дальше можно не решать. Выражение не имеет смысла.
Если под корнем всё нормально, плюс, а в результате извлечения получается заведомый минус - сделайте из него плюс! Этого требуют правила действий с квадратными корнями.
Ну вот, основные тонкости корней мы разобрали. Теперь об одной ошибке. Эта ошибка ничего общего с тонкостями не имеет! Это абсолютно тупой косяк, о котором и говорить-то неловко. Но надо. Слишком часто он встречается...
Обратите внимание! Все свойства корней связаны с умножением-делением. И ни одного - со сложением-вычитанием! На сложение-вычитание корней - не существует специальных формул!
Однако бывает:
![]()
или:
![]()
Хотя одинаковые корни можно, конечно, складывать-вычитать. Как приводить подобные с буквами. Например:
![]()
или:
![]()
Но эти действия к специфическим свойствам корней не имеют никакого отношения.
А теперь попрактикуемся в корнях. От примитивных заданий до продвинутых. Все ответы даны в беспорядке.
Вычислить:
![]()
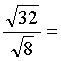
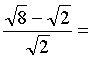
Ответы: 1, 9, 2.
Упростить:
![]()
![]()
![]()
Ответы: 3а4 b, -4а4 b5 , 3а.
Вычислить (все буквы - неотрицательные):
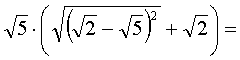
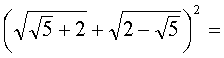
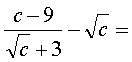
![]()
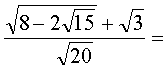
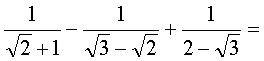
Ответы (в беспорядке): выражение не имеет смысла; 5; 4; 1; -3; 0,5





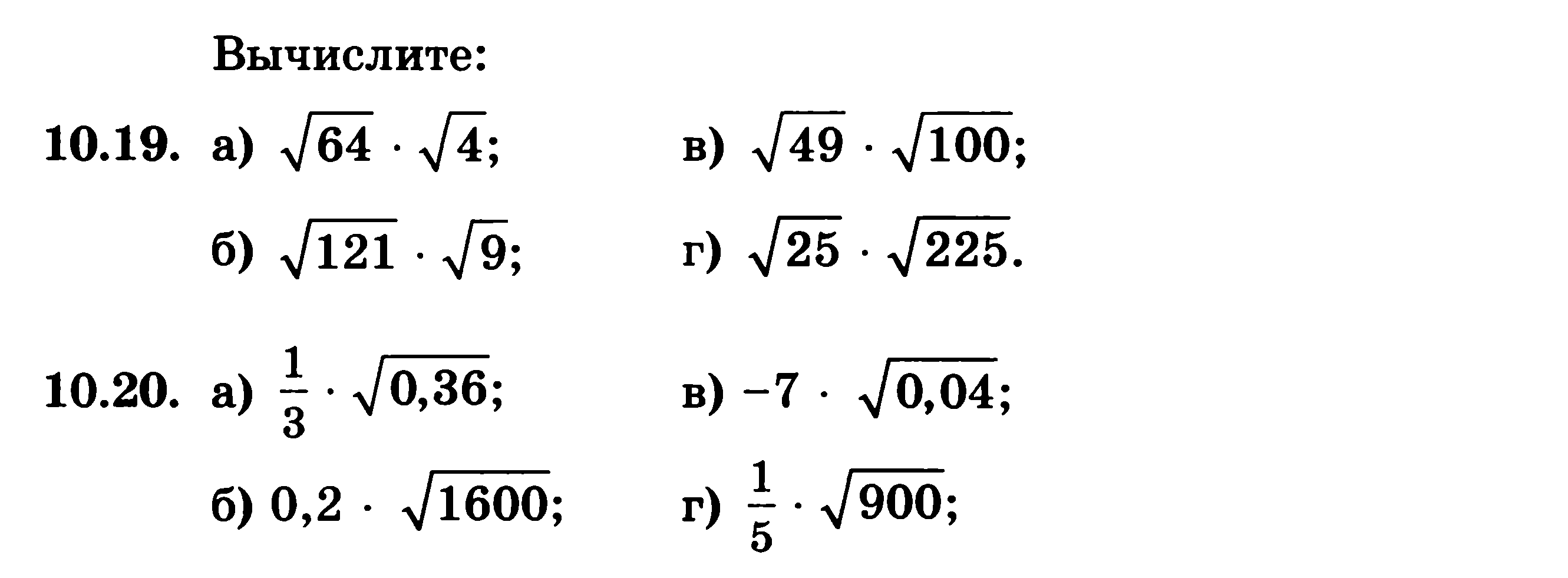
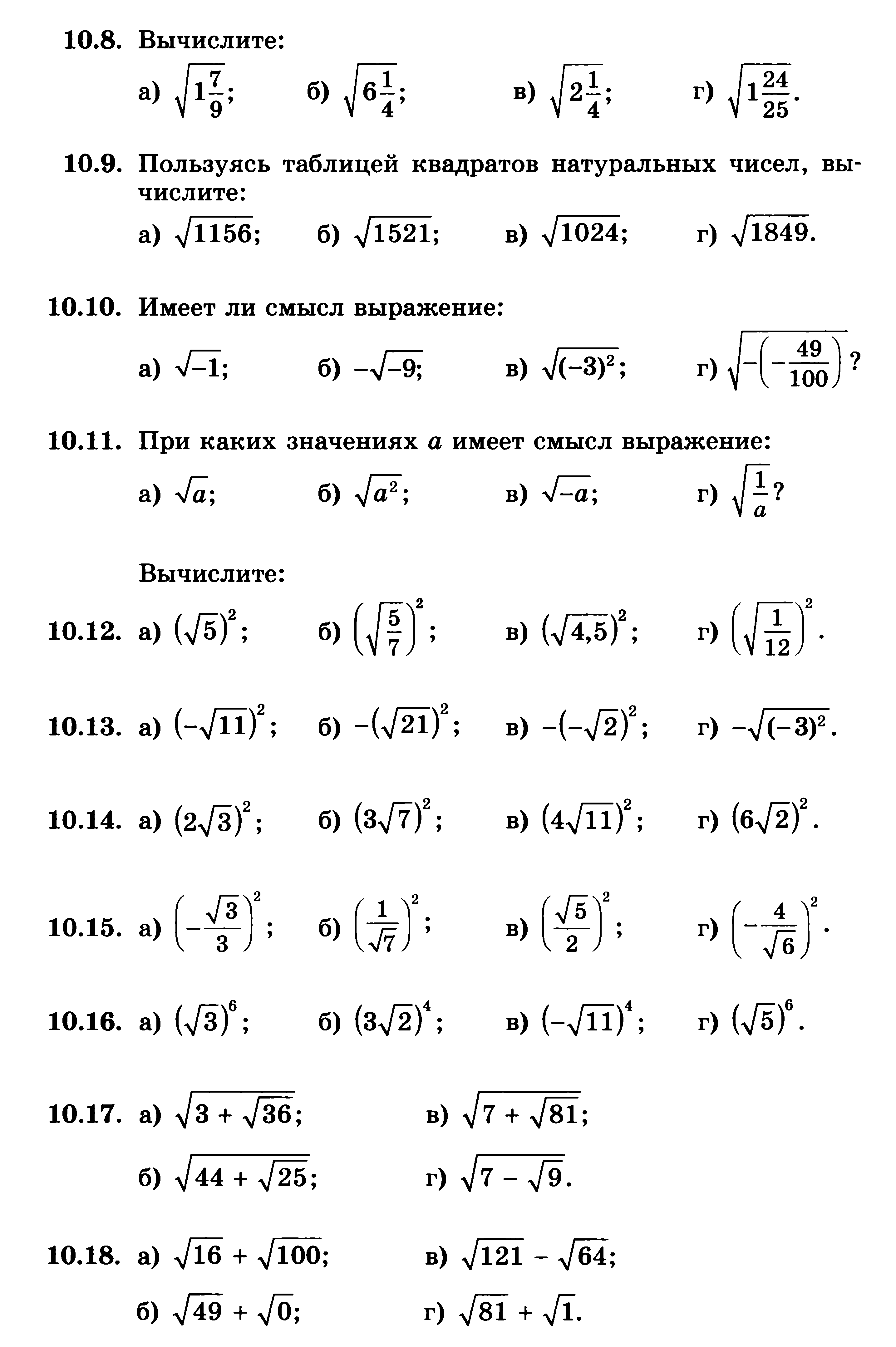
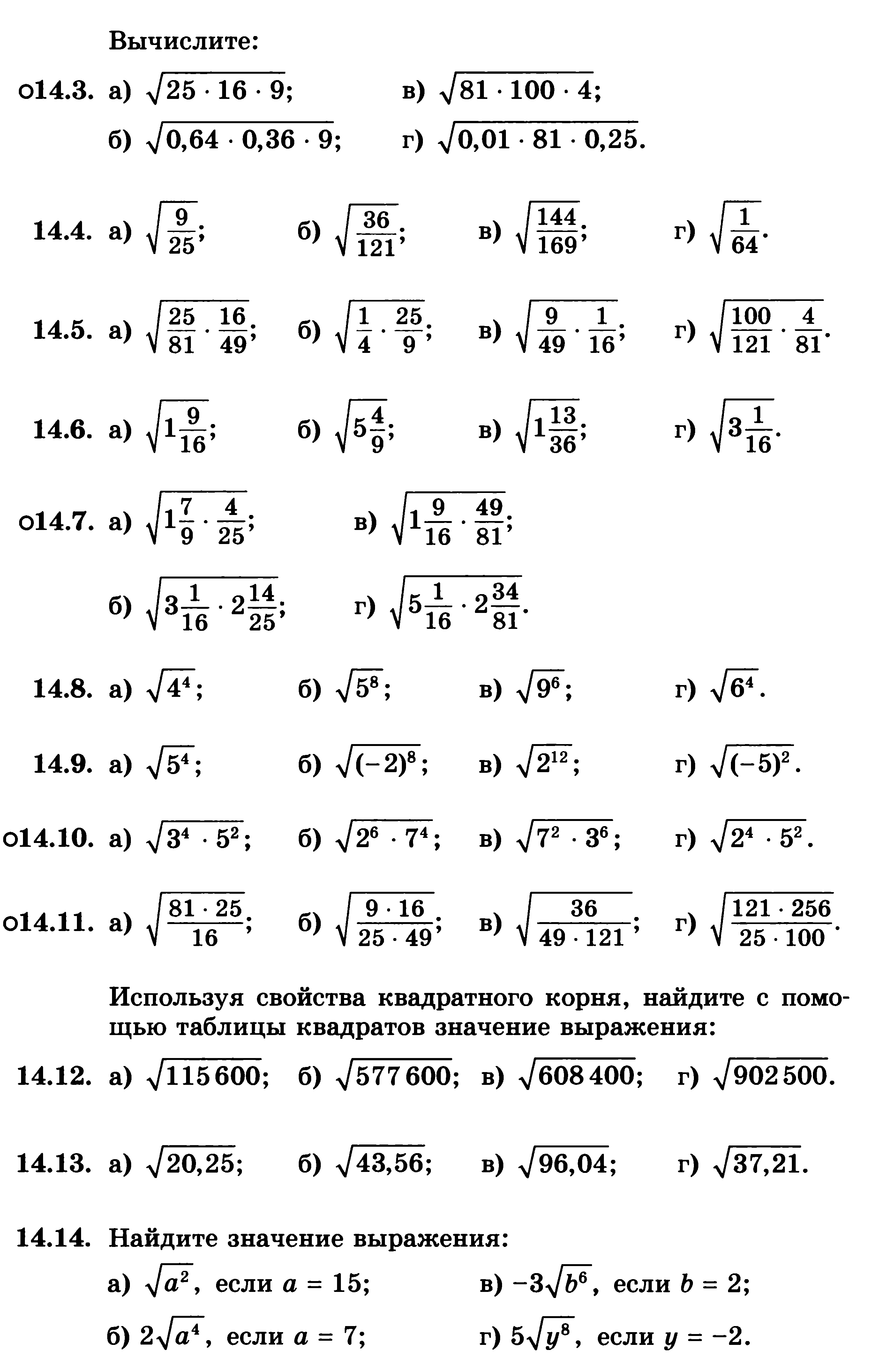
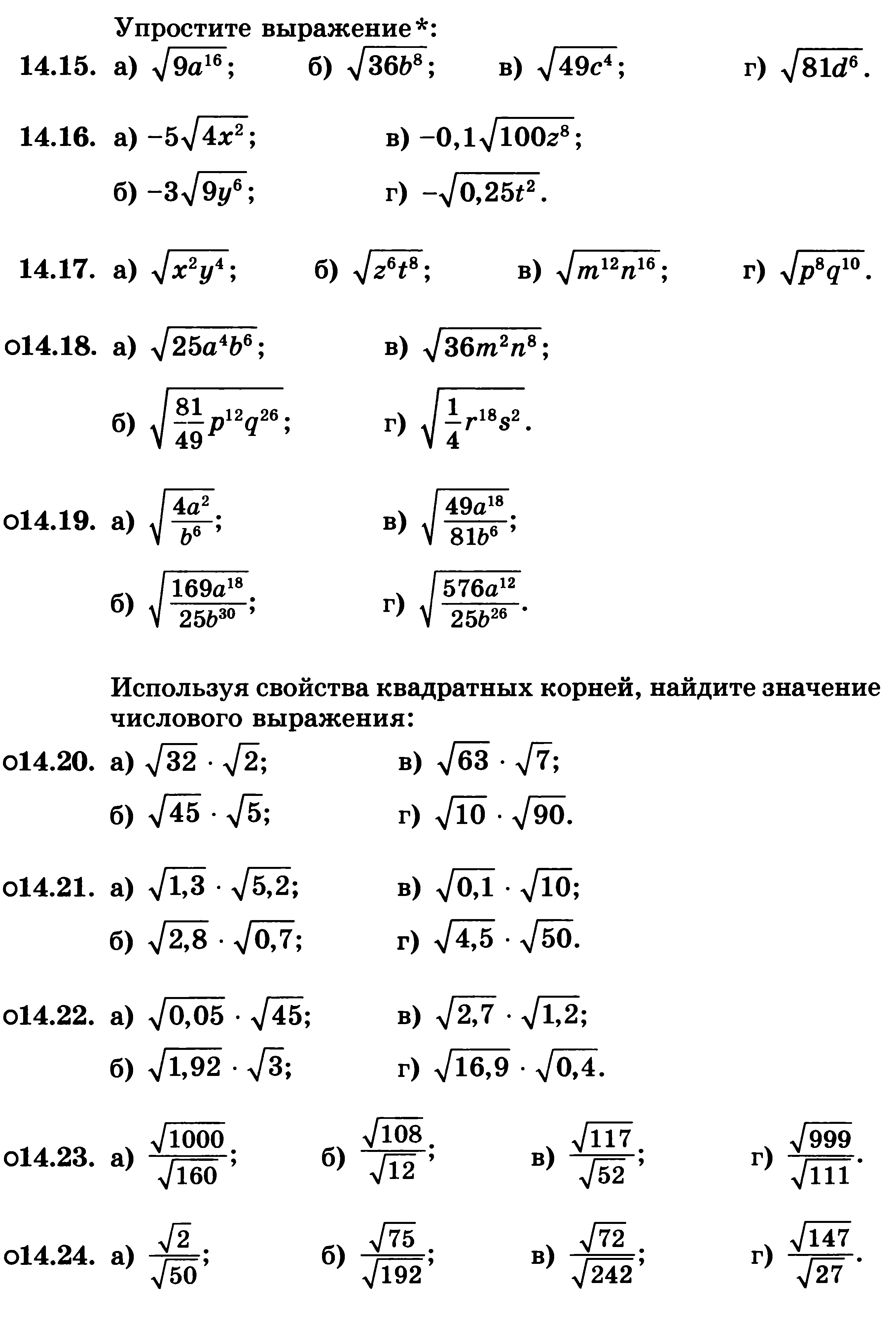

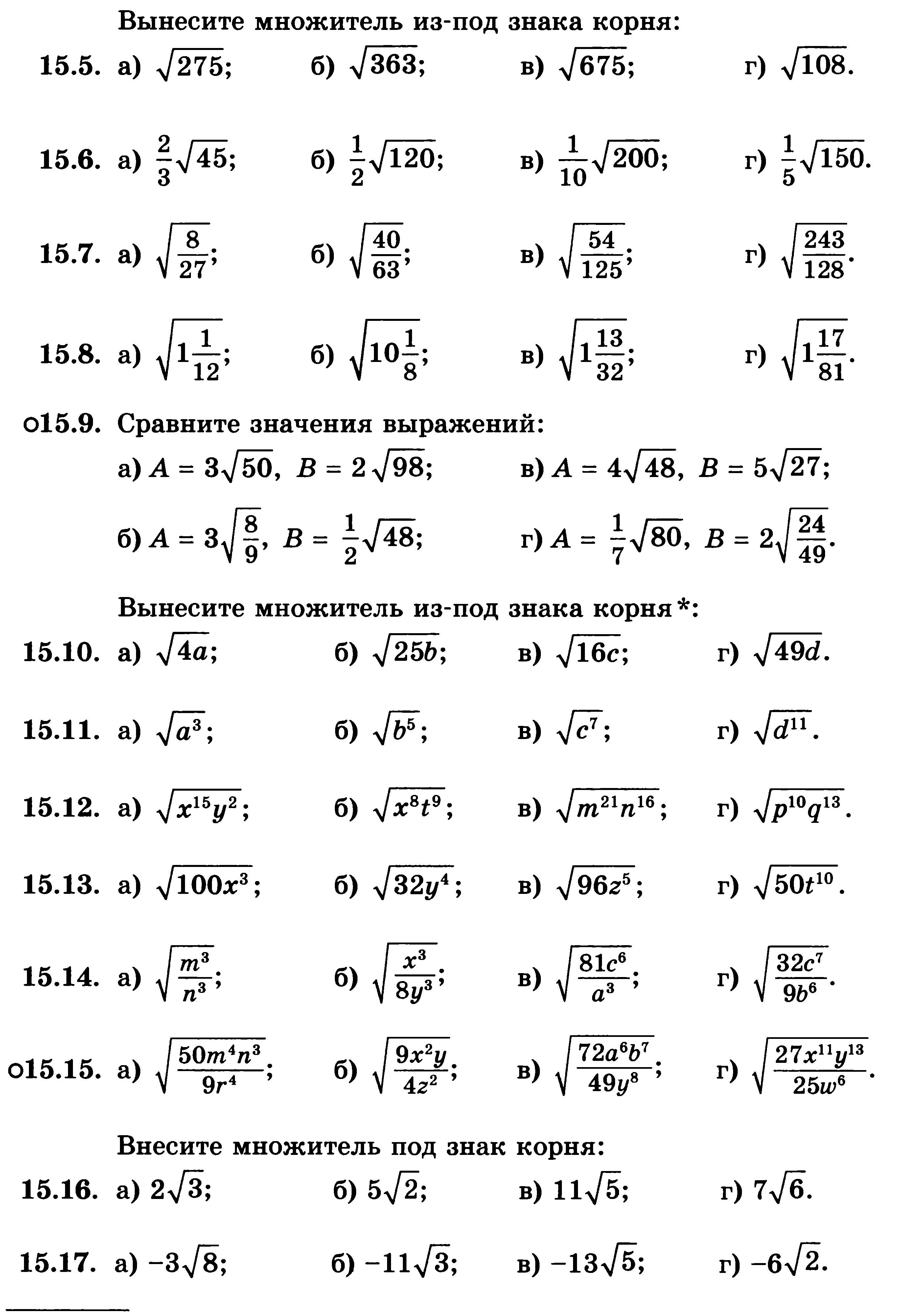
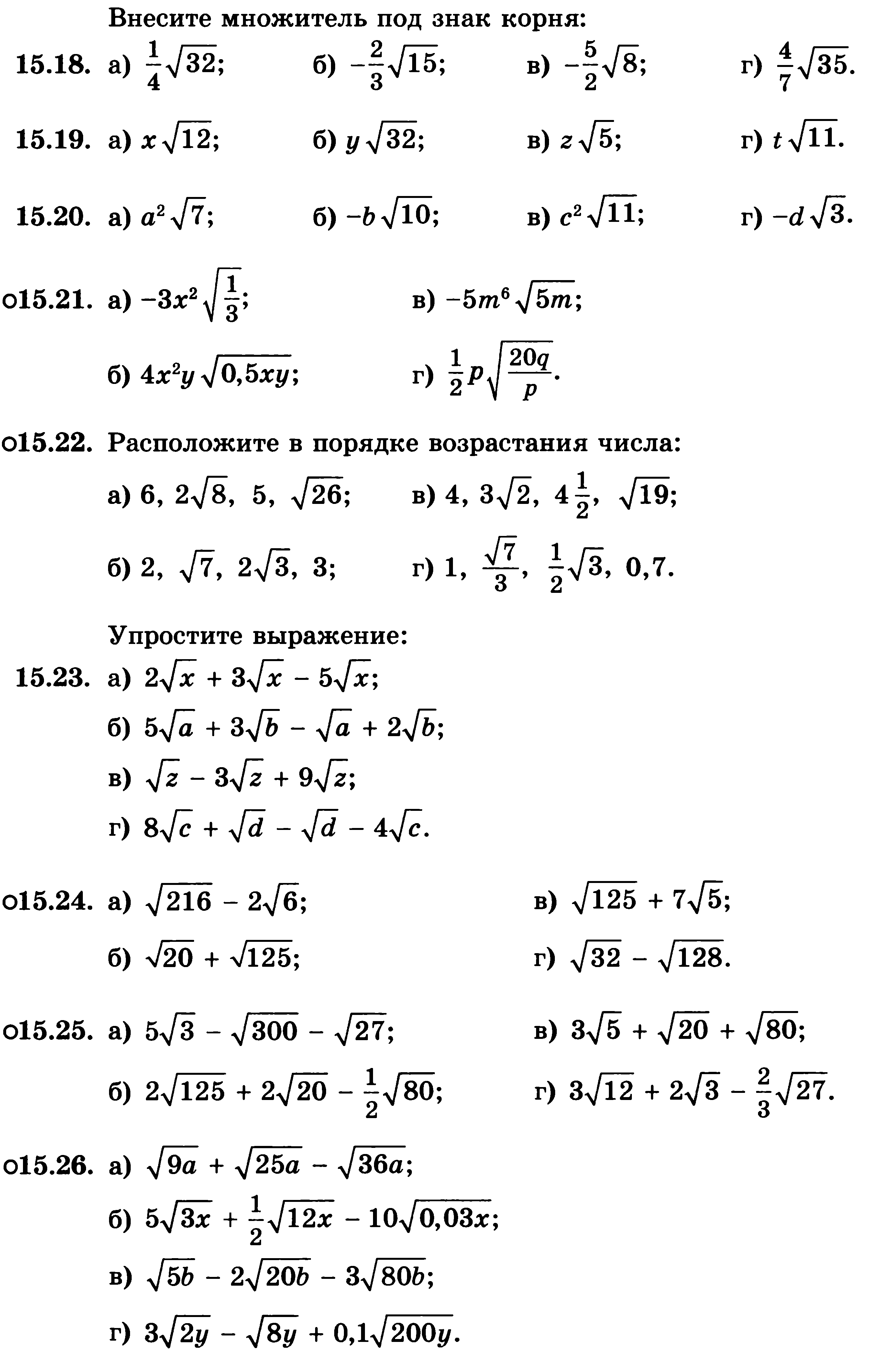

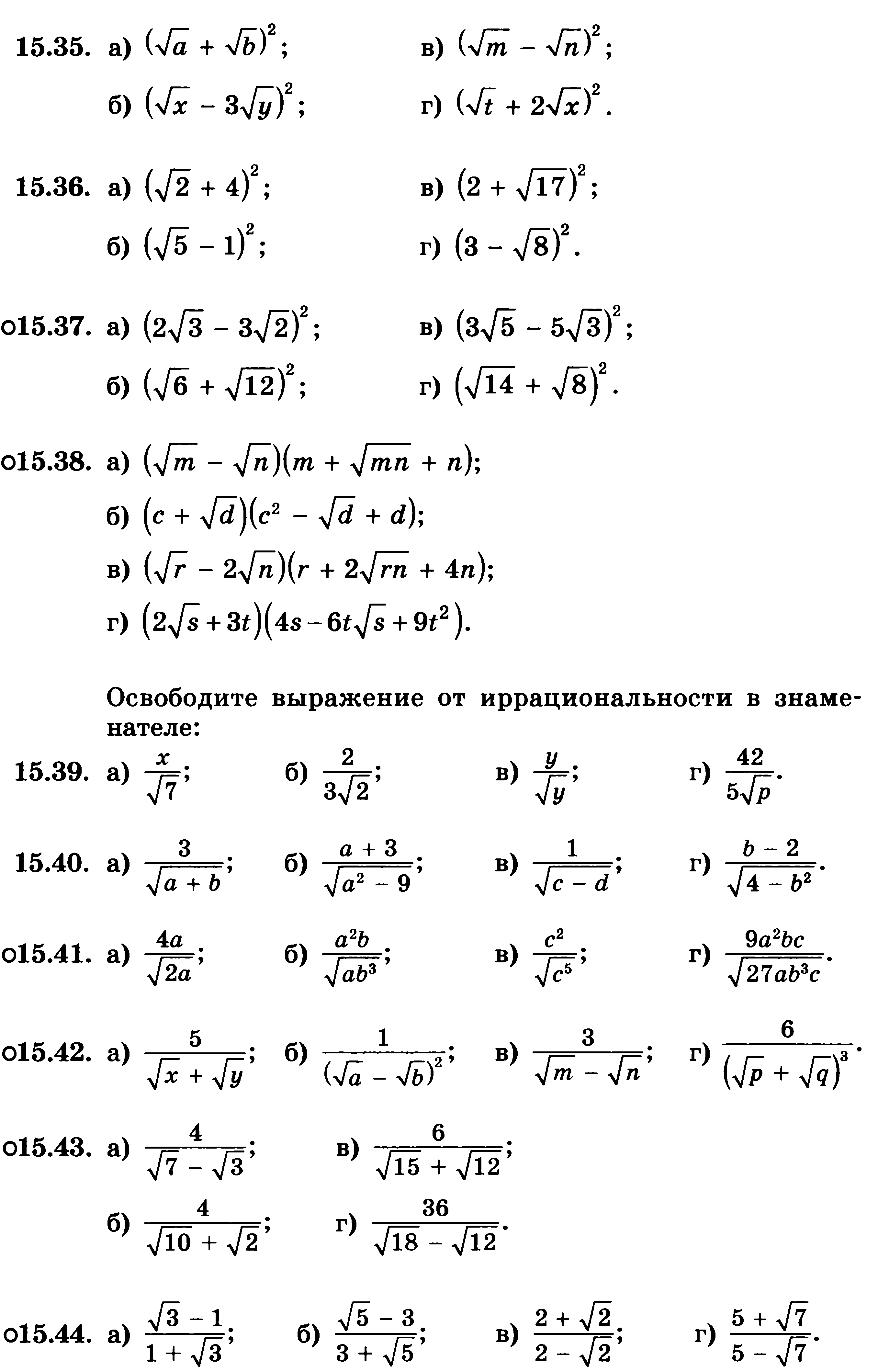
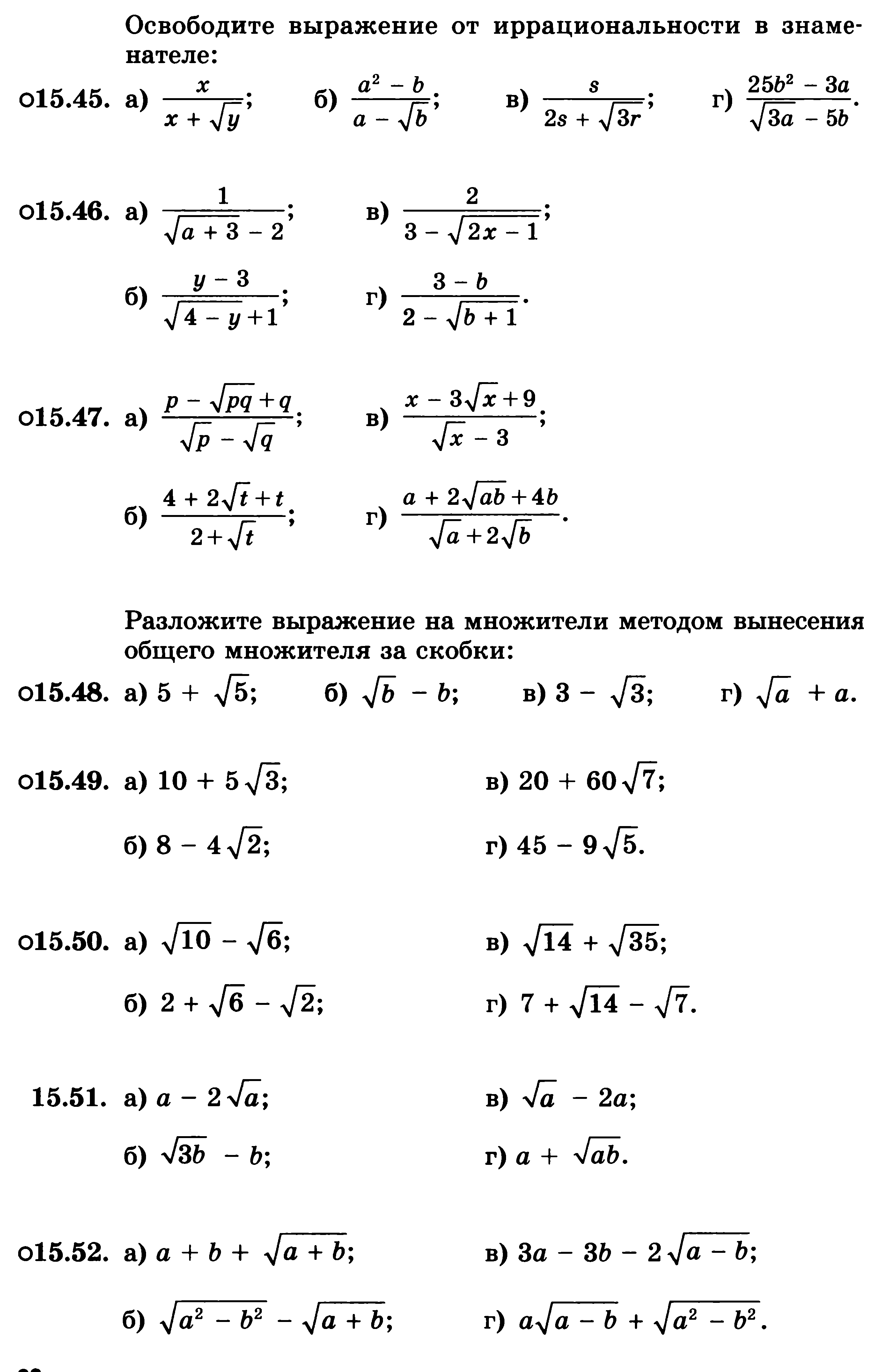
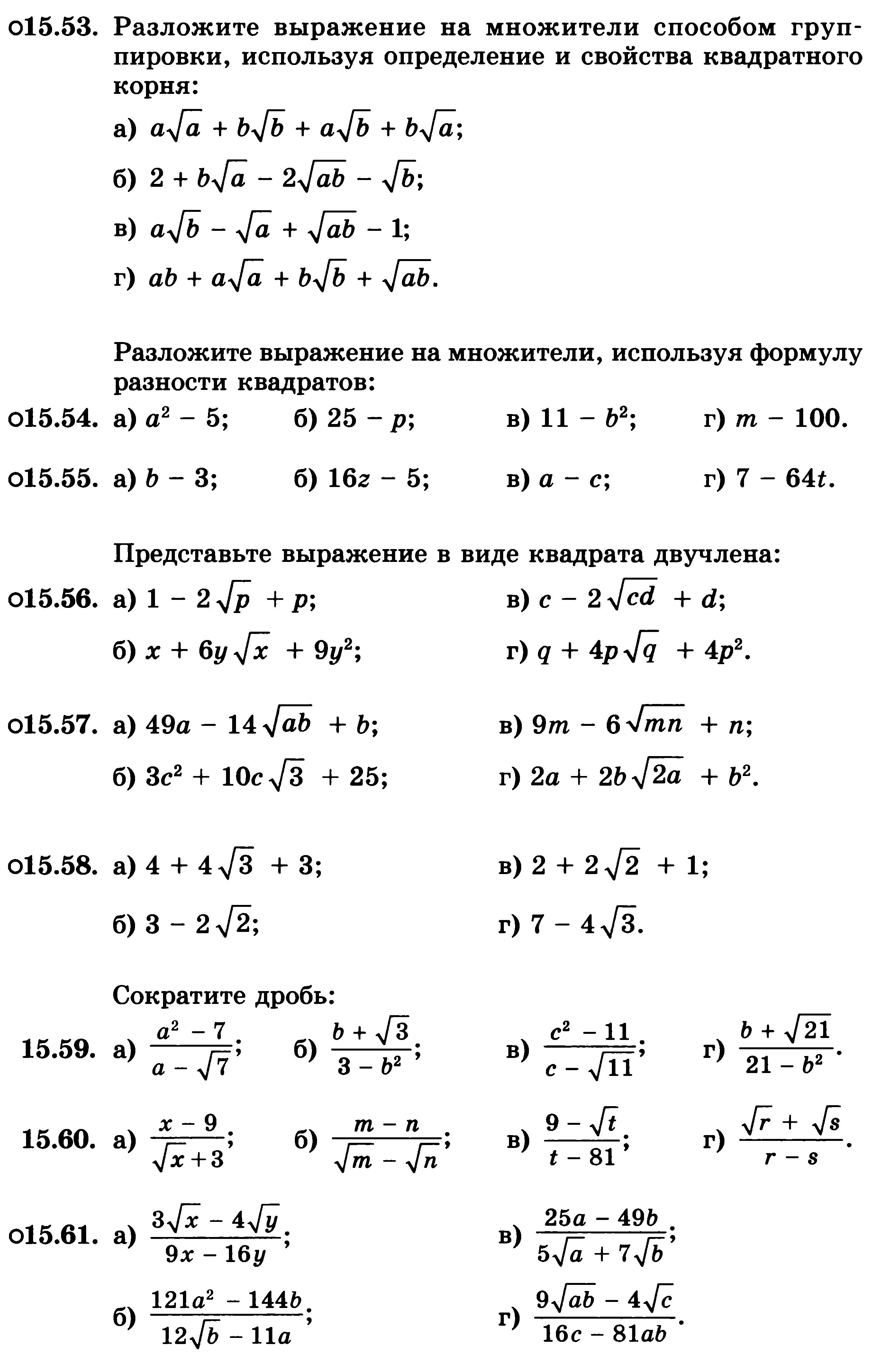
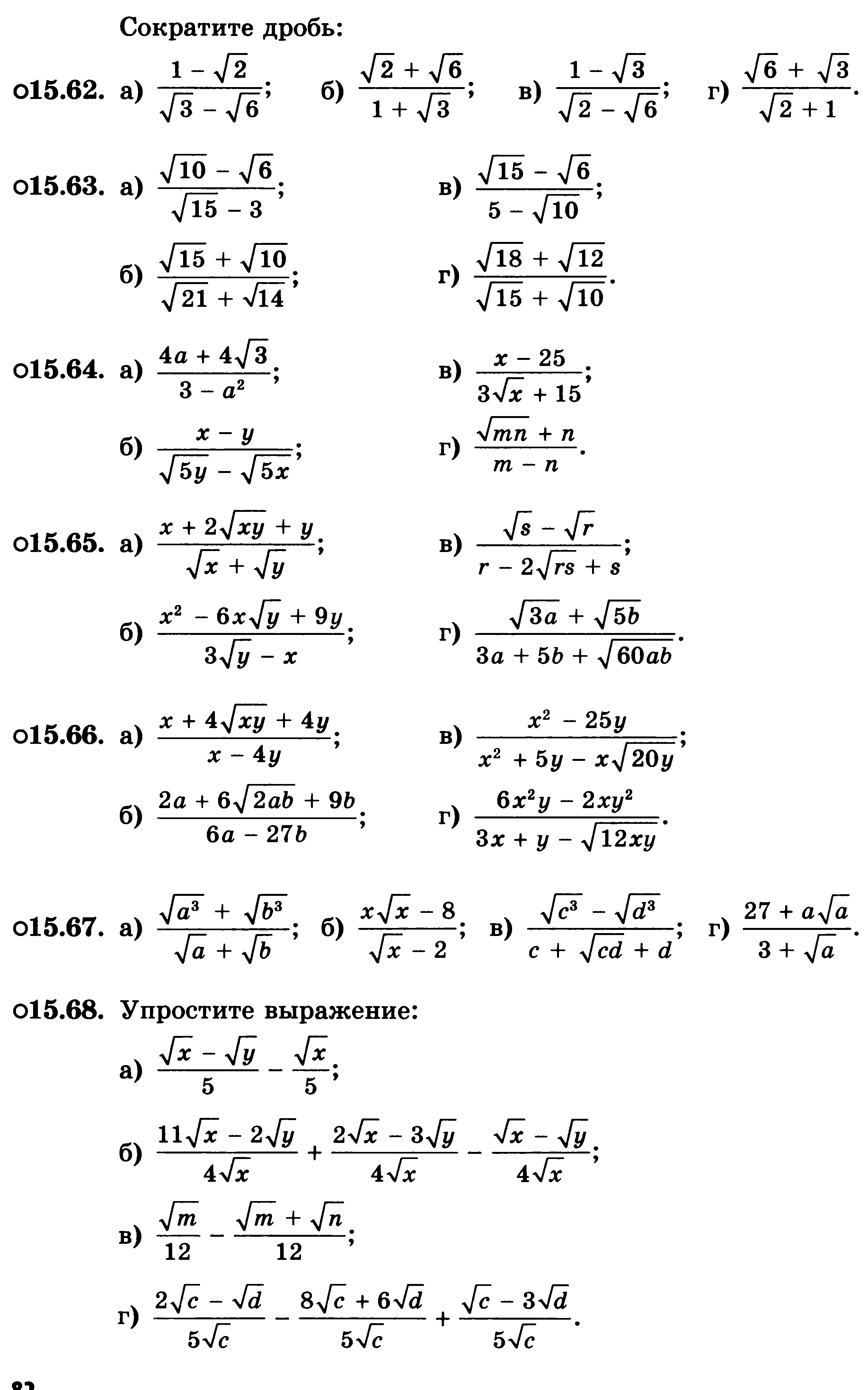
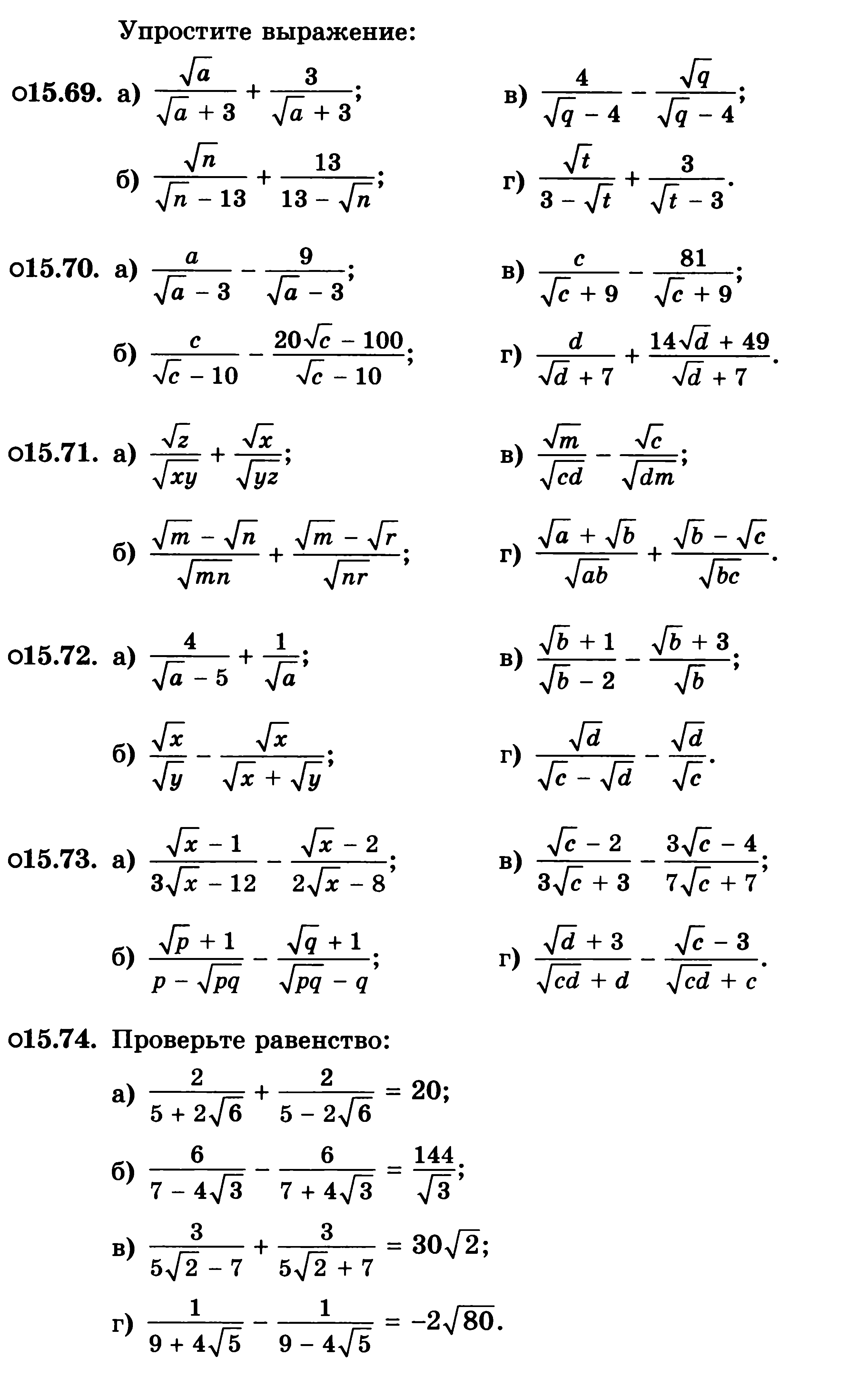
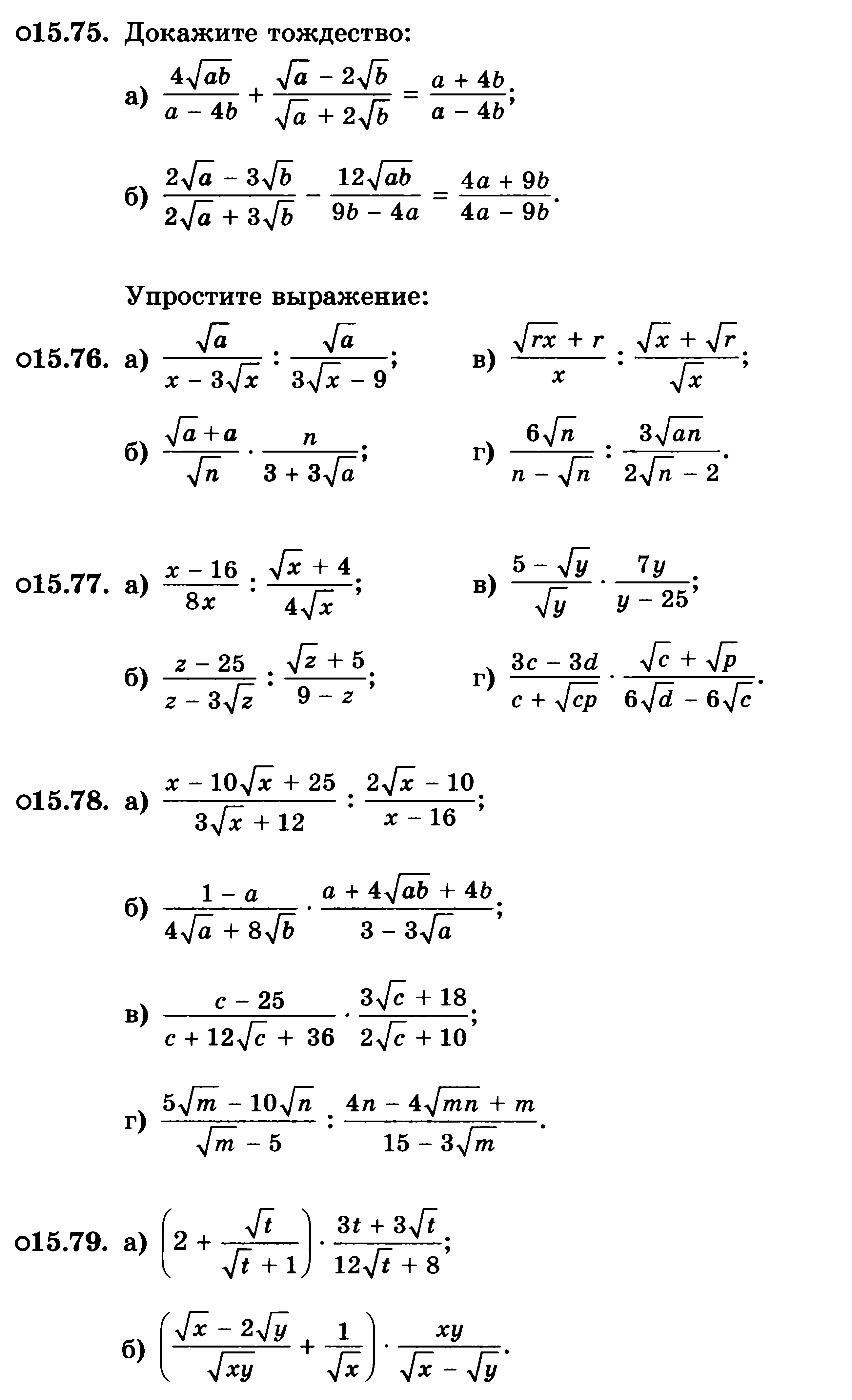
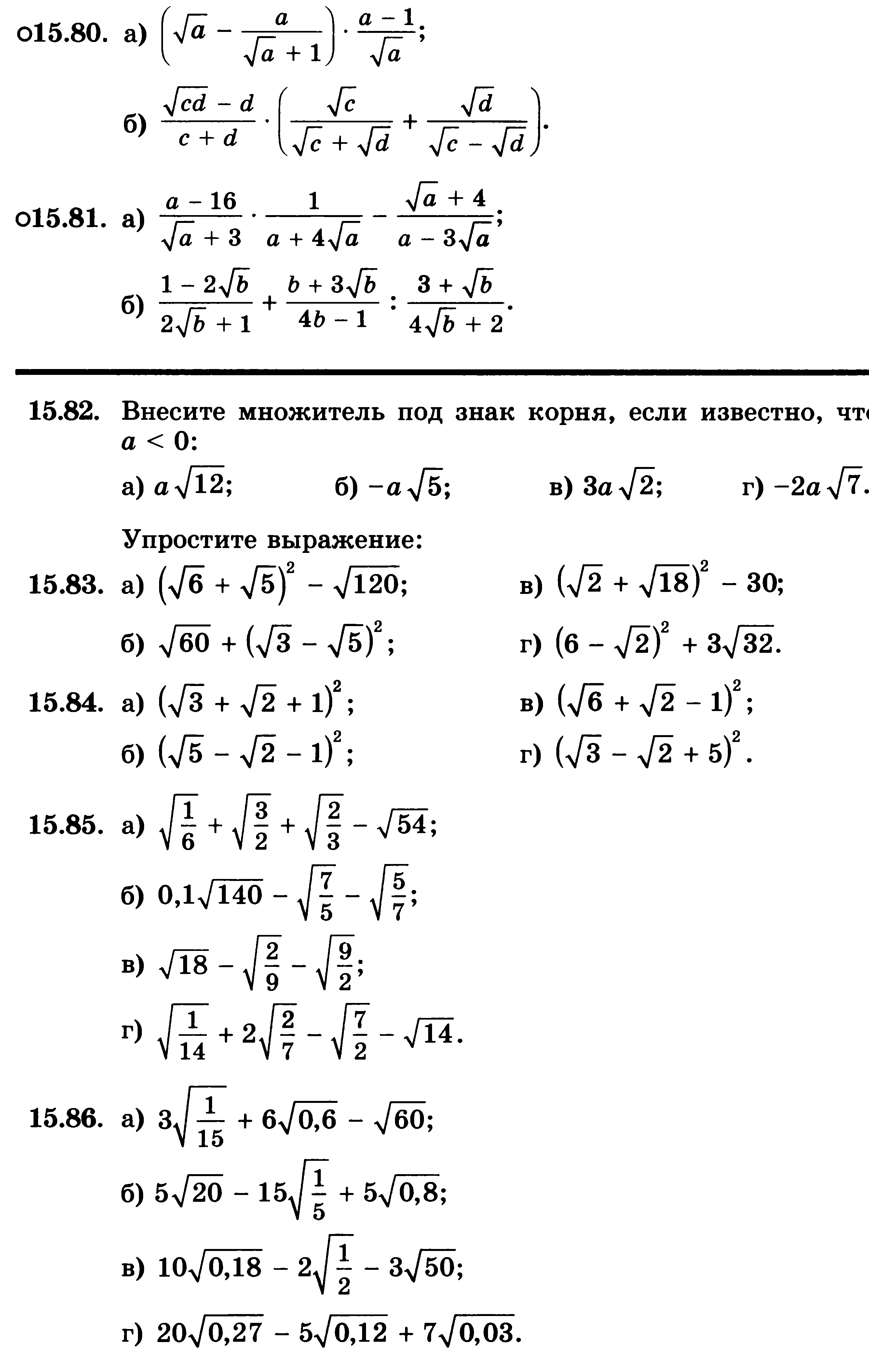
A1.
Вычислите
![]() .
.
1) 7; 2)
![]() ;
3) 5; 4)
;
3) 5; 4)
![]() .
.
А 2. Вычислите
![]() .
.
1) 7; 2) ; 3) ; 4) 4.
A3.
Внесите множитель под знак корня
![]() .
.
1)
![]()
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
А 4.Вынесите множитель
из-под знака корня 0,2
![]() .
.
1) 0,1![]() ;
2)
;
2)
![]() ;
3) 0,5
;
4)
.
;
3) 0,5
;
4)
.
А5.
Исключить иррациональность из знаменателя
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3) 4 (
);
4) 4.
;
3) 4 (
);
4) 4.
А
6. Найдите значение выражения
![]() при х = 5.
при х = 5.
1) 4; 2) 16; 3) ; 4) 10.
А 7. Упростите
выражение
![]() ,
а>0,
в> 0.
,
а>0,
в> 0.
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
A1.
Вычислите
![]() .
.
1) 2; 2)6; 3) 4; 4) .
А 2. Вычислите
![]() .
.
1) 2; 2)6; 3) 4; 4) .
A3.
Внесите
множитель под знак корня
![]() .
.
1)
;
2)
;
3)![]() ;
4)
;
4)![]() .
.
А4.Вынесите множитель
из-под знака корня
![]()
![]() .
.
1) 3![]() ;
2) 9
;
3) 3
;
2) 9
;
3) 3![]() ;
4)
.
;
4)
.
А 5. Исключить
иррациональность из знаменателя
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3) 3 (
);
4) 3.
;
3) 3 (
);
4) 3.
А 6. Найдите значение выражения при х = - 5.
1) 4; 2) 6; 3) ; 4) 36.
А
7. Упростите выражение
![]() ,
а>0,
в> 0.
,
а>0,
в> 0.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
