
Как извлекать корни из больших чисел?
Вспоминаем формулу извлечения корней из произведения. Ту, что я чуть выше написал. Но где у нас произведение!? У нас огромное число 6561 и всё... Да, произведения здесь нет. Но если нам надо - мы его сделаем! Разложим это число на множители. Имеем право.
Для начала сообразим, на что делится это число ровно? Что, не знаете!? На 3 и на 9 делится это число. Потому, что сумма цифр (6+5+6+1=18) делится на эти числа. Это один из признаков делимости. На три нам делить ни к чему, а вот на 9 поделим. Хотя бы и уголком. Получим 729. Вот мы и нашли два множителя! Первый - девятка (это мы сами выбрали), а второй - 729 (такой уж получился). Уже можно записать:
![]()
Улавливаете идею? С числом 729 поступим аналогично. Оно тоже делится на 3 и 9. На 3 опять не делим, делим на 9. Получаем 81. А это число мы знаем! Записываем:
![]()
Всё получилось легко и элегантно! Корень пришлось по кусочкам извлекать, ну и ладно. Так можно поступать с любыми большими числами. Раскладывать их на множители, и - вперёд!
Кстати, а почему на 3 делить не надо было, догадались? Да потому, что корень из трёх ровно не извлекается! Имеет смысл раскладывать на такие множители, чтобы хотя бы из одного корень хорошо извлекался. Это 4, 9, 16 ну, и так далее. Делите своё громадное число на эти числа поочерёдно, глядишь, и повезёт!
Но не обязательно. Может и не повезти. Скажем, число 432 при разложении на множители и использовании формулы корней для произведения даст такой результат:
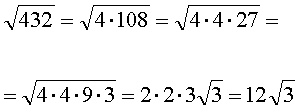
Ну и ладно. Всё равно мы упростили выражение. В математике принято оставлять под корнем самое маленькое число из возможных. В процессе решения все зависит от примера (может и без упрощения всё посокращается), а вот в ответе надо дать результат, который уже дальнейшему упрощению не поддаётся.
Кстати, знаете, что мы с вами сейчас с корнем из 432 сделали?
Мы вынесли множители из-под знака корня! Вот так называется эта операция. А то попадётся задание - "вынести множитель из-под знака корня" Вот вам ещё одно применение свойства корней. Полезная вещь пятая.
Как вынести множитель из-под корня?
Легко. Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:
![]()
Ничего сверхъестественного. Важно правильно выбрать множители. Здесь мы разложили 72 как 36·2. И всё получилось удачно. А могли разложить иначе: 72 = 6·12. И что!? Ни из 6, ни из 12 корень не извлекается... Что делать?!
Ничего страшного. Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:
![]()
Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:
![]()
Перемножать всё - сумасшедшее число получится! И как потом из него корень извлекать?! Опять на множители раскладывать? Не, лишняя работа нам ни к чему. Сразу раскладываем на множители и собираем одинаковые по кучкам:
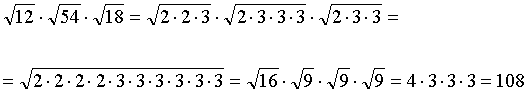
Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать.
Всего одно свойство корней, одна небольшая формула умножения корней - и какие разнообразные возможности для практического применения!
Формула умножения корней позволяет:
-умножать корни,
-вносить число под корень,
-сравнивать корни,
-извлекать корни из больших чисел,
-выносить множитель из-под корня.
И все эти возможности вытекают из одной небольшого свойства корней.
В нашем арсенале есть ещё два свойства корней. Одно - простое, второе - не очень. Но разобраться с ними можно и нужно.
Переходим к следующей формуле. Это будет деление корней.
Формула столь же проста, как и умножение. Вот она:
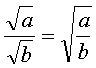
Напоминаю: здесь а - неотрицательное число (больше или равно нулю), b - положительное (больше нуля)! Иначе формула смысла не имеет... Об этих тонкостях мы ниже поговорим.
У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.
