3 Решение систем линейных уравнений

Метод простой итерации

В этом методе исходная система уравнений Ах=В приводится к виду x=Cx+D, выбирается начальное приближение и каждое следующее приближение определяется по формуле .

Условие сходимости: или

Алгоритм приведения системы уравнений к виду, пригодному для метода итераций:

• выбрать уравнения, в которых коэффициент при одном неизвестном превышает сумму модулей коэффициентов при других неизвестных;

• выполнить алгебраические преобразования так, чтобы в остальных уравнениях коэффициент при одном неизвестном превышал сумму модулей коэффициентов при других неизвестных (причем максимальный коэффициент в каждом уравнении должен быть при разных переменных);

• максимальный коэффициент в каждом уравнении представить в виде разности, уменьшаемое в которой кратно 10;

• слагаемые с коэффициентом, кратном 10 перенести в левую часть уравнений, остальные – в правую;

• разделить все уравнения на коэффициент, стоящий в левой части урвнений;

• проверить условие сходимости для каждого уравнения.

ЗАДАЧА 3.

Привести систему уравнений к виду, пригодному для метода итераций.

РЕШЕНИЕ.

Приведем систему уравнений к виду x=Cx+D

Выберем уравнение, в котором коэффициент при одном неизвестном превышает сумму модулей коэффициентов при других неизвестных: x₁– 4х₂+2х₃=4. Умножим левую и правую часть уравнения на –1, получим уравнение: –x₁ + 4х₂ – 2х₃=–4.

Выполним алгебраические преобразования так, чтобы в остальных уравнениях коэффициент при одном неизвестном превышал сумму модулей коэффициентов при других неизвестных (причем максимальный коэффициент в каждом уравнении должен быть при разных переменных).

Сложив первое и второе уравнения, получим: 5x₁+ 3х₂+х₃=28.

Умножив второе уравнение на 2 и сложив с третьим, получим: 5x₁– 2х₂+ 8х₃=34.

Поменяв уравнения местами, получим систему уравнений, эквивалентную заданой:

Максимальный коэффициент в каждом уравнении представим в виде разности, уменьшаемое в которой кратно 10:

Слагаемые с коэффициентом, кратном 10 перенесем в левую часть уравнений, остальные – в правую:

Разделим все уравнения на коэффициент, стоящий в левой части урвнений (на 10):

Проверим условие сходимости:

0,5 + 0,3 + 0,1 = 0,9 < 1

0,1 + 0,6 + 0,2 = 0,9 < 1

0,5 + 0,2 + 0,2 = 0,9 < 1

Таким образом, полученная система уравнений удовлетворяет условию сходимости.

Задание 3.

Привести систему уравнений к виду, пригодному для метода итераций.

4 Приближение функций

Метод Лагранжа заключается в построении полинома n-порядка при n+1 узле интерполяции на отрезке [x₀,x_n] по формуле: L(x)=y₀ Q₀(x)+…+ y_n Q_n(x),

где

Qj(x_i)=0 при ij и Qj(x_i)=1 при i=j

Метод Ньютона заключается в построении полинома n-порядка при n+1 узле интерполяции на отрезке [x₀,x_n], используя конечные разности.

Конечной разностью первого порядка называется разность между значениями функции в соседних узлах интерполяции: Из конечных разностей первого порядка можно образовать конечные разности второго порядка и т.д.

Общая формула для вычисления конечной разности k-ого порядка в i-ой точке:

Для интерполяции в начале таблицы и экстраполяции назад удобно использовать первую интерполяционную формулу Ньютона:

, где

Для интерполяции в конце таблицы и экстраполяции вперед рекомендуется использовать вторую интерполяционную формулу Ньютона:

, где

Погрешность интерполяции можно оценить по формуле

где .

ЗАДАЧА 4.1.

Вычислить с помощью формулы Лагранжа для трех узлов интерполяции. Определить погрешность вычисления.

РЕШЕНИЕ

В качестве узлов интерполяции выберем точки, близкие к заданному значению аргумента, в которых значения функции можно вычислить точно: х₀=100; х₁=121; х₂=144

i	0	1	2
x	100	121	144
y	10	11	12

При трех узлах интерполяции имеем следующую формулу Лагранжа:

При х=117

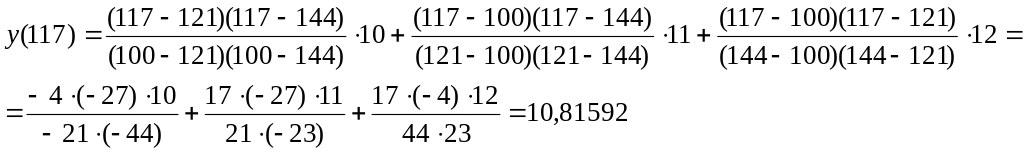
ЗАДАЧА 4.2.

Функция задана таблично:

x	2,0	2,1	2,2	2,3	2,4	2,5	2,6
y	1,1	0,9	0,85	0,7	0,63	0,5	0,3

Оценить погрешность метода Ньютона по последней конечной разности:

1) у(2,05) 2) y(2,23) 3) y(2,38)

РЕШЕНИЕ

Составим таблицу конечных разностей:

x 2 2,1 2,2 2,3 2,4 2,5 2,6

y 1,1 0,9 0,85 0,7 0,63 0,5 0,3

∆y -0,2 -0,05 -0,15 -0,07

∆2y 0,15 -0,1 0,08

∆3y -0,25 0,18

∆4y 0,41

h=0,1

1) y(2,05)

Заданное значение аргумента находится в начале таблицы, поэтому используем первую интерполяционную формулу Ньютона при x₀=2,0

q=(2,05-2,0)/0,1=0,5

Последней конечной разностью в первой строке является ∆⁴y, т.е. n+1=4

Из таблицы находим, что М₄=0,41. Тогда

2) y(2,23)

Используем первую интерполяционную формулу Ньютона при x₀=2,2

Последней конечной разностью во второй строке (движение выделено подчеркиванием) является ∆²y, т.е. n+1=2

Из таблицы находим, что М₃=0,25. Тогда

3) y(2,38)

Заданное значение аргумента находится в конце таблицы, поэтому используем вторую интерполяционную формулу при

Последней конечной разностью (движение выделено цветом) является ∆⁴y, т.е. n+1=4

Из таблицы находим, что М₄=0,41. Тогда

ЗАДАЧА 4.3.

Найти значение функции, определенной в задании 4.2, используя полином Ньютона 2-ого порядка в точках 1) 2,05 2) 2,23 3) 2,38.

1) у(2,05)=1,1+(-0,2) · 0,5+0,15 · 0,5 · (0,5–1)/2=0,98125≈0,98

2) ≈0,81

3) ≈0,76

Задание 4.1. Вычислить с помощью формулы Лагранжа значение у для трех узлов интерполяции. Определить погрешность вычисления.

1) 2) y=38³

Задание 4.2.

Функция задана таблично:

x	0,1	0,2	0,3	0,4	0,5	0,6
y	0,03983	0,07926	0,11791	0,15542	0,19146	0,22575

Найти у(0,58), у(0,08), у(0,35) и оценить погрешность