5.2. Линейные однородные уравнения
Определение 1. Дифференциальное уравнение вида
(5.2)
где
-
функции, непрерывные на некотором
интервале (a,b),причем
ни
в одной точке этого интервала называется
линейным однородным .
С
помощью линейного оператора L,
определенной формулой 
уравнение (5.2) можно записать как
Пользуясь линейным оператором L, легко доказать следующие свойства решений уравнений (5.2).
Теорема
1. Пусть
u(x)
и
-два
решения уравнения
.
Тогда:
Функция
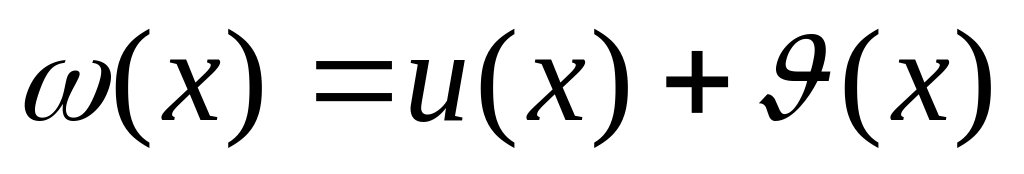также
будет решением этого уравнения,Для любого действительного числа
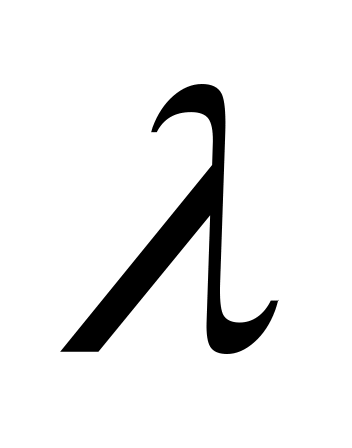функция
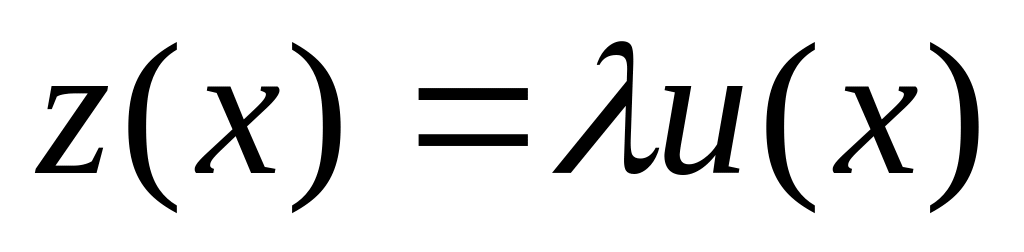будет решением уравнения
Определение2. Любая линейно независимая система из n решений линейного однородного уравнения (5.2) называется фундаментальной системой решений этого уравнения.
Теорема 2. Для любого линейного однородного уравнения (5.2)существует фундаментальная система решений.
Теорема 3. Любые (n-1)решений уравнения образуют линейно зависимую систему.
5.3.Линейные неоднородные уравнения
Теорема 1. Общее решение линейного неоднородного уравнения (5.1)
может быть представлено в следующем виде
(5.3)
где
образуют фундаментальную систему
решений соответствующего однородного
уравнения, a
u(x)
–некоторое фиксированное частное
решение неоднородного уравнения.
5.4. Линейные однородные уравнения с постоянными коэффициентами
Определение
1.
Функции 
фигурирующие в уравнении (5.1), т.е.
называются коэффициентами этого уравнения. До сих пор предполагалось, что эти коэффициенты – непрерывные на (a,b) функции.
В этом подразделе рассмотрим частный, но весьма важный, случай линейных уравнений: случай, когда коэффициенты не зависят от x, т.е. постоянны.
Итак, будем изучать линейные дифференциальные уравнения вида
(5.4)
Где
- действительные числа (
коэффициент при 
без ограничения общности можно считать
равным единице). Естественно, что все
результаты, полученные для уравнения
с переменными коэффициентами, остаются
справедливыми и для этих уравнений. В
поисках частных решений, необходимых
для построения фундаментальной системы
решений и формулы общего решения, обычно
обращаются к функциям вида 
.
Если подставить эту функцию в однородное
уравнение
(5.5)
То с учетом формулы
Получим
Определение 2. Многочлен
называется характеристическим многочленом уравнения или дифференциального оператора L, который можно представить как линейную комбинацию операторов дифференцирования разных порядков:
Полученные в результате подстановки функции уравнение имеет вид
Если
к- действительное число, то 
Сокращая на 
,
получим уравнение относительно к:
Это алгебраическое уравнение степени n называется характеристиками уравнением, а его корни – характеристическими корнями уравнения или соответствующего дифференциального оператора.
Если
к
таково, что 
,то
функция
будет решением однородного уравнения.
Поэтому нахождение характеристических
корней уравнения приводит к нахождению
частных решений однородного уравнения.
На
этом пути появляется возможность найти
n
частных решений, которые могли бы
составить фундаментальную систему
решений. Дело в том, что по основной
теореме алгебры алгебраическое уравнение
n-й
степени имеет ровно n
корней, если каждый корень считать
столько раз, какова его кратность.
Поэтому первый случай, когда имеется n
различных решений, просматривается
сразу: это случай, когда все корни
действительны и различны:
при 
.
Тогда получаем n
различных частных решений:
Убедимся в том, что эта система решений линейно независима.
Для этого рассмотрим линейную комбинацию этих решений
Пусть
она тождественно равна нулю. Выберем
из чисел 
наибольшее (пусть это будет
)
и разделим равенство
на
.
Получим
При увеличении x все слагаемые, начиная со второго, имея отрицательное число при x показателе степени, стремятся к нулю.
Отсюда
следует, что 
.
Рассуждая
аналогично, получим, что все числа
должны быть равными нулю. Следовательно,
система решений:
линейно независима, т.е. образует
фундаментальную систему решений. Поэтому
общее решение однородного уравнения в
этом случае будет иметь вид
(5.6)
Пример1.
Пусть требуется найти общее решение
дифференциального уравнения
.
Составляем
характеристическое уравнение
Решая
его, находим характеристические корни:
Функции
образуют фундаментальную систему
решений. Общее решение имеет вид
Рассмотрим
случай, когда характеристический
многочлен раскладывает на линейные
множители:
где все 
различны. По образцу этого разложения
можно разложить и дифференциальный
оператор
Допустим
теперь, что два корня совпадают, например,
Тогда оператор можно записать в виде
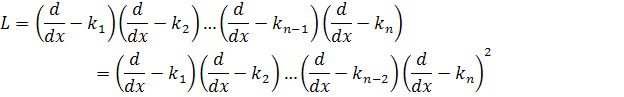
Если
найти функцию 
такую, что 
,
то, очевидно , и 
т.е.
будет решением исходного однородного
уравнения.
Рассмотрим
подробнее уравнение
,
Или
Введем в рассмотрение новую неизвестную функцию
или
и подставим ее в это уравнение. Имеем:
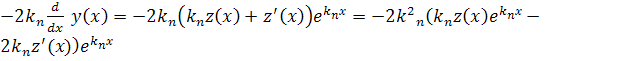
Складывая
левые и правые части последних трех
равенств, получим, что функция 
является решением уравнения
Сокращая
на множитель 
, в итоге имеем уравнение
Его общее решение легко находится двумя последовательными интеграциями:
Следовательно, общее решение уравнения
имеет вид
,
Откуда
видно, что функции
и 
будут решениями этого уравнения. Таким
образом , в случае совпадения двух корней
(кратность корня 
равно двум) им соответствует два решения:
и
.
Пример2.Пусть требуется найти общее решение уравнения
Характеристическое уравнение имеет вид
Разлагая характеристический многочлен на множители, получим
Откуда
.
Фундаментальная система решений имеет
вид:
.
Следовательно, общее решение дается
формулой
В интегральном исчислении обычно используется разложение многочлена на множители (без использования комплексных чисел). Многочлен с действительными коэффициентами всегда может быть разложен на множители также с действительными коэффициентами. Это множители могут быть линейными, как. Например, в приведенном примере, или квадратичными, т.е. имеет вид
.
В
этом случае выделением полного квадрата
можно преобразовать множитель:
где
.
Соответствующий дифференциальный
оператор имеет вид
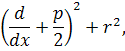
и, решая дифференциальное уравнение
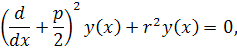
Найдем
частные решения однородного уравнения,
порождаемые множителем
.
Решение этого уравнения, проводиться
по той же схеме. Что и выше: вводиться
неизвестная функция
И
в уравнении производиться замена
на
.
Для функции 
уравнение
упрощается и имеет следующий вид:
Это
уравнение не содержит переменного 
и
можно понизить его порядок, а затем -
проинтегрировать. Получим, что общее
решение этого уравнения представляется
в виде
Возвращаясь
к функции
,получим
Таким
образом, множитель 
d
в характеристическом многочлене
порождает пару решений однородного
уравнения:
которые должны быть включены в фундаментальную систему решений.
Подробное доказательство этого факта технически громоздко и малопоучительно с идейной точки зрения. Поэтому здесь его не приводим.
Рассмотренный случай разобран при молчаливом предположении, что все квадратичные множители различны, но может оказаться, что среди них попадутся одинаковые. Тогда эти одинаковые множители можно собрать в один. Записав его в виде
где
и доказать, что этому множителю
характеристического многочлена в
фундаментальной системе решений
соответствует следующая группа частных
решений
Пример3. Пусть требуется найти общее решение следующего дифференциального уравнения:
Характеристический многочлен
можно представить в виде
Выписывая фундаментальную систему решений, найдем общее решение:
.
Таким образом, на основе вышеизложенного можно сделать вывод. Что решение линейного однородного дифференциального уравнения с постоянными коэффициентами всегда доводиться до общего решения, если удается разложить характеристический многочлен на линейные и квадратичные множители. Эта последняя задача относиться к алгебре, и здесь ее обсуждать не будем.
Задания для закрепления. Решить уравнения:
;
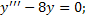
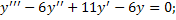
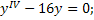
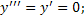
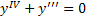