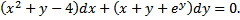2.7 Уравнения Бернулли
Определение 1. Уравнением Бернулли называется уравнение вида
,
(2.6)
где
a
– произвольное число, не равное 0
и 1.
Это уравнение сводиться к линейному
уравнению с помощью замены z=
.
Действительно,
делением уравнения (2.6) на 
приводим
ее к виду:
Теперь
замечаем, что левая часть уравнения в
точности равна 
.
После умножения уравнения на
(1-α)
получаем линейное уравнение:
(2.7)
которое может быть решено по схеме, приведенной в п. 2.6.
Замечание.
Если α>0,
то при делении уравнения на 
происходит потеря решения 
,
которое
следует также учесть.
Пример. Решим уравнение Бернулли:
.
Здесь
α=3.
Делаем замену z=
.
Уравнения
после умножения на
и
замены переменного
примет
вид
Решаем
его с помощью вариации постоянной:
p(x)=4x,
откуда P(x)=
q(x)
.
H(x)
=
откуда
.
Заменяя z после несложных преобразований, придем к формуле
,
Охватывающий
все решения уравнения, кроме одного:
y
,
которое
следует также учесть, так
как
Задания для закрепления:
Найти общее решение уравнений:
2.8. Уравнения в полных дифференциалах
Определение 1. Уравнением в полных дифференциалах называется дифференциалом уравнения первого порядка следующего вида:
P(x,y)dx + Q(x,y)dy=0 ( 2.8)
Если его левая часть предоставляет собой полный дифференциал функции двух переменных. Если функция P(x,y) и Q(x,y) имеют непрерывные частные производные, то для того чтобы уравнение (11.8) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество
.
(2.9)
Это условие легко проверяется, и если оно выполнено, то существует функция U(x,y) такая, что dU=P(x,y)dx+Q(x,y)dy. Следовательно, уравнение имеет вид dU(x,y)=0, и его общий интеграл будет U(x,y)=C,
Где С - произвольная постоянная. Остается невыясненным вопрос, как найти функцию это можно сделать несколькими способами. Один из них приводит к следующей формуле:
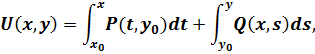
где
производная точка
принадлежит
области, в которой выполняются указанные
выше условия для функции P(x,y)
и
Q(x,y).
Доказательство здесь не приводим. Итак,
общий интеграл уравнения(2.8) при выполнении
условия (2.9) имеет следующий вид:
где С- произвольная константа.
Замечания.
1)
Естественно, что, зная частные производные,
можно восстановить функцию 
только
с точностью до постоянного слагаемого.
Внешне выражения для общего интеграла
могут быть разными, но множество решений
при этом не измениться.
2) Произвольность постоянной С, стоящей в правой части общего интеграла, ограничивается интервалом изменения значений функций .Например, если общий интеграл имеет вид
то C может принимать любые значения только из отрезка [-1,1], поскольку
Пример. Рассмотрим уравнение
Здесь
Проверим выполнение условия (2.9). Имеем
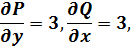
т.е. условие(2.9) выполняется. Находим функцию
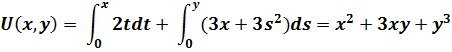
[в качестве точки взяли точку (0,0)]. Общий интеграл имеет вид
Задания для закрепления:
Найти общее решение уравнений:
;
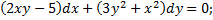
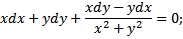
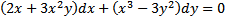