1.4. Разрешимость задачи Коши
Определение 1. Пусть Пᵪ - множество точек (х, у) на плоскости, удовлетворяющих условию х˳ ≤ х ≤ Х, −∞ < у < +∞; это множество назовем полосой.
Теорема
11.1. Пусть
функция
определена и непрерывна в полосе Пᵪ и
удовлетворяет условию
Липшица:
существует постоянная L
такая,
что для любого х
[x˳,Х]
и любых у₁
и у₂
выполняется неравенство │ 
≤ L
│
│.
(11.3)
Тогда
для любого начального значения y˳
решение
задачи Коши найти решение уравнения
удовлетворяющего условию 
,
существует и единственно на всем
отрезке
.
(Без доказательства).
Замечание:
Если
функция
имеет
в полосе
частную производную
такую, что существует постоянная L
такая, что для любого
и любого у
выполняется
неравенство
,
То условие Липшица выполнено.
Пример. Рассмотрим уравнение
Здесь
Функция
имеет
и
Следовательно,
при любых
и Х
задача
Коши имеет единственное решение на
отрезке
.
2. Уравнения первого порядка, интегрируемые в квадратурах
2.1.
Уравнения
вида
=
Пусть
функция f(x)
непрерывна на интервале (a, b).
Тогда, как известно из курса интегрального
исчисления, если 
и 
принадлежат этому интервалу, то одним
из решений рассматриваемого
дифференциального уравнения
=f(x)
будет функция
Y(x)
=
Все другие решения отличаются от него на постоянное слагаемое. Поэтому общим решением будет функция
Y(x)
=
+С
Пример. Найти общее решение уравнения
Имеем
(
где
=
С-
будет произвольной константой, поскольку
таковой является С.
Задания для закрепления:
Найти общее решение уравнений:
;
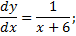
2.2.
Уравнения вида
=
Это уравнение в том случае, когда f(у) непрерывна и не обращается в нуль на интервале (a, b), можно переписать в форме (поменяв ролями х и у)
,
что позволяет свести уравнение к виду рассмотренному выше (см.п. 2.1). Его общий интеграл будет иметь вид
x=
[
и у принадлежат интервалу (a, b)].
Если же в какой-либо одной точке 
этого интервала окажется, что f(
=0,
то интервал (a, b)
распадается на два интервала (а,
)
и (
,b),
на каждом из которых может быть найден
общий интеграл и , кроме того, возникает
еще одно решение y=
Пример. Найти общий интеграл уравнения
=
.
Переписываем уравнение в виде
=
,
или
=
.
Откуда получаем
X=
=
-
,
где
=
С+
- произвольная константа.
Задания для закрепления:
Найти общее решение уравнений:
2.3. Уравнения с разделенными переменными
Определение 1. Уравнением с разделенными переменными называется уравнение вида:
F(x) dx + g(y )dy = 0, (2.1)
где коэффициент f зависит только от х, а g – только от у, т.е. переменные разделены.
Будем считать, что функция f(x) и g(y) непрерывны на интервалах (а, b) и (c, d) соответственно. Его можно переписать в следующем виде:
d
=0,
т.е. как дифференциал от функции двух переменных: х и у. Здесь и х принадлежат интервалу (а, b), а и y –интервалу (c ,d). Таким образом, функция. Стоящая под знаком дифференциала, определена и дифференцируема внутри прямоугольника a<x<b, c<y<d. Функция, имеющая первый дифференциал, тождественно равный нулю в прямоугольнике, является в этом прямоугольнике константой. Поэтому тождество эквивалентно тождеству
=С.
Поскольку оно не содержит производных, то представляет собой общий интеграл уравнения. Его можно записать в виде F(x,y)=С. Произвольность постоянной С ограничивается интервалом изменения функции F(x,y).
Пример:
Найти общий интеграл уравнения
.
Решение:
Данное уравнение есть ДУ с разделенными
переменными. Поэтому
Обозначим
.
Тогда 
- общий интеграл ДУ.
Задания для закрепления:
Найти общее решение уравнений:
