
Тема 5. Корреляционный метод
115. Задание {{ 116 }} ТЗ-1-111.
Наиболее тесную связь показывает коэффициент корреляции rxy = … .
rxy = 0,982
rxy = 0,991
rxy = 0,871
116. Задание {{ 117 }} ТЗ-1-112.
Обратную связь между признаками показывают коэффициенты корреляции rxy
rxy = = 0,982
rxy = =-0,991
rxy = =0,871
117. Задание {{ 118 }} ТЗ-1-113.
Прямую связь между признаками: показывают
коэффициенты корреляции rху
rху = 0,982
rху =-0,991
rху =0,871
118. Задание {{ 119 }} ТЗ-1-114.
Межгрупповая дисперсия составляет 61% от общей дисперсии.
Эмпирическое корреляционное отношение = ... (с точностью до 0,01).
Правильные варианты ответа: 0,78;
119. Задание {{ 120 }} ТЗ-1-115.
Простейшим приемом выявления корреляционной связи между двумя признаками является ... .
расчет коэффициента корреляции знаков
расчет коэффициента эластичности
построение уравнения корреляционной связи
корреляционное поле
120. Задание {{ 121 }} ТЗ-1-116.
Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения ... .
средней из групповых дисперсий к общей дисперсии
межгрупповой дисперсии к общей дисперсии
межгрупповой дисперсии к средней из групповых дисперсий
средней из групповых дисперсий к межгрупповой дисперсии
121. Задание {{ 122 }} ТЗ-1-117.
Теснота связи двух признаков при нелинейной зависимости определяется по формуле ... .

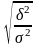

122. Задание {{ 123 }} ТЗ-1-118.
Для корреляционных связей характерно ... .
разным значениям одной переменной соответствуют различные средние значения другой
с изменением значения одной из переменных, другая изменяется строго определенным образом
связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более
123. Задание {{ 124 }} ТЗ-1-119.
Тесноту связи между двумя альтернативными признаками можно измерить с помощью коэффициента ... .
знаков Фехнера
корреляции рангов Спирмена
ассоциации
контингенции
конкордации
124. Задание {{ 125 }} ТЗ-1-120.
Парный коэффициент корреляции показывает тесноту ... .
линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель
линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель
тесноту нелинейной зависимости между двумя признаками
связи между результативным признаком и остальными, включенными в модель
125. Задание {{ 126 }} ТЗ-1-121.
Частный коэффициент корреляции показывает тесноту ... .
линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель
линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель
нелинейной зависимости
связи между результативным признаком и остальными, включенными в модель
126. Задание {{ 127 }} ТЗ-1-122.
Парный коэффициент корреляции может принимать значения ... .
от 0 до 1
от -1 до 0
от -1 до 1
любые положительные
любые меньше нуля
127. Задание {{ 128 }} ТЗ-1-123.
Частный коэффициент корреляции может принимать значения ... .
от 0 до 1
от -1 до 0
от -1 до 1
любые положительные
любые меньше нуля
128. Задание {{ 129 }} ТЗ-1-124.
Множественный коэффициент корреляции может принимать значения ... .
от 0 до 1
от -1 до 0
от -1 до 1
любые положительные
любые меньше нуля
129. Задание {{ 130 }} ТЗ-1-125.
Коэффициент детерминации может принимать значения ... .
от 0 до 1
от -1 до 0
от -1 до 1
любые положительные
любые меньше нуля
130. Задание {{ 131 }} ТЗ-1-126.
Коэффициент детерминации равен ... коэффициента корреляции.
квадрату множественного
квадратному корню из множественного
квадрату парного
квадрату частного
корню из парного
131. Задание {{ 132 }} ТЗ-1-127.
Коэффициент детерминации характеризует ... .
долю дисперсии результативной переменной, обусловленной влиянием независимых переменных, входящих в модель
остаточную дисперсию
дисперсию результативной переменной
долю дисперсии результативной переменной, обусловленной влиянием всех неучтенных в модели факторов
долю дисперсии результативной переменной, обусловленной влиянием наиболее весомого в модели фактора
132. Задание {{ 133 }} ТЗ-1-128.
Прямолинейная связь между факторами исследуется с помощью уравнения регрессии ... .
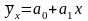



133. Задание {{ 134 }} ТЗ-1-129.
Для аналитического выражения нелинейной связи между факторами используются формулы ... .
134. Задание {{ 135 }} ТЗ-1-130.
Для изучения связи между двумя признаками рассчитано
линейное уравнение регрессии:
параметры:
Параметр
 показывает, что:
показывает, что:
связь между признаками прямая
связь между признаками обратная
с увеличением признака "х" на 1 признак "у" увеличивается на 0,694
с увеличением признака "х" на 1 признак "у" увеличивается на 0,016
135. Задание {{ 136 }} ТЗ-1-131.
Для изучения связи между двумя признаками рассчитано
линейное уравнение регрессии:
параметры:
Параметр показывает, что:
связь между признаками прямая
связь между признаками обратная
с увеличением признака "х" на 1 признак "у" увеличивается на 36,5
с увеличением признака "х" на 1 признак "у" уменьшается на 1,04
