Утвержден

А.В.00001-01 33 01-1-ЛУ

Решение системы n-линейных уравнений с n-переменными пояснительная записка содержание

ВВЕДЕНИЕ 3

1. ОБЩАЯ ЧАСТЬ 4

Введение

В настоящее время компьютеры широко применяются в самых разных областях: науке, промышленности, медицине, образовании. Применение компьютеров в системе образования значительно облегчает труд преподавателя, так как позволяет быстрее и легче проверить знания учащихся, подготовить для них обучающие и тестовые задания. Применение компьютеров способствует также повышению уровня знаний студентов.

Разработанная в данном курсовом проекте программа решения СЛАУ может быть использована в учебных заведениях, в которых курс математики включает изучение решения СЛАУ. Программа позволит преподавателю быстро решить тестовые примеры, предлагаемые студентам.

Программа может быть также использована в различных инженерных и научных расчетах, требующих решения СЛАУ.

1. Общая часть

1.1. Описание предметной области

Система n линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

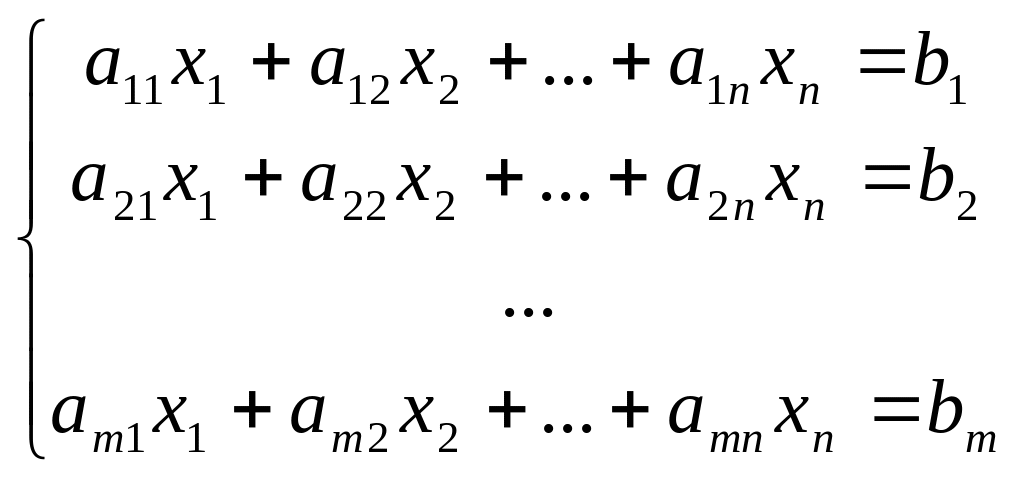(1.1.1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1.1.1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1.1.1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1.1.1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1.1.1) обращает все ее уравнения в тождества.

Система (1.1.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система вида (1.1.1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1.1.1) называются различными, если нарушается хотя бы одно из равенств: , , …,

Совместная система вида (1.1.1) называется определённой, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Изучение способов решения систем линейных уравнений входит в программу курса математики многих высших учебных заведений.

Разрабатываемая программа позволит быстро решить данную систему линейных уравнений.

1.2. Анализ методов решения

Решение системы линейных уравнений может быть реализовано следующими способами:

• Ручным — этот способ является трудоёмким и требует больших затрат времени.

• Автоматизированным — исходные данные вводятся вручную, а результат рассчитывается программой на компьютере.

• Автоматическим — исходные данные автоматически считываются с внешнего устройства (например, файла на диске) и обрабатываются программой.

Для решения системы уравнения можно использовать следующие методы:

• Прямые (или точные) методы, которые позволяют найти решение за определенное количество шагов;

• Итерационные методы, которые основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

К прямым методам решения относятся:

• Матричный метод;

• Метод Гаусса

• Метод Гаусса – Жордана

• Метод Крамера

К итерационным методам решения относятся:

• Метод Гаусса – Зейделя

• Метод релаксации

• Метод простой итерации (м. Якоби)

• Многосеточный метод