1.Выборочная ковариация. Основные правила расчета ковариации. Теоретическая ковариация. Недостаток ковариации как меры связи.

Выборочная ковариация – мера зависимости между двумя переменными.

Основные правила расчета ковариации

1. Y= v + w, Cov(x,y) = cov(x,v)+ cov(x,w)

2. Y=a*z, a-const, cov(x,y) =a*cov(x,z)

3. Y = a, a – const, cov(x,y) = 0

Теоретическая ковариация. Если x и y случайные величины, то теоретическая ковариация – мат. Ожидание произведения отклонения этих величин от их средних значений.

-теоретические значения x и y соотв.

Недостаток ковариации как меры связи. Ковариация зависит от единиц, в кот. измеряются переменные x и y .

2.Коэффициент корреляции. Частный коэфф. корреляции.

Теоретический коэфф. корреляции.

Выборочный (частный) коэфф. корреляции

3.однофакторная линейная регрессионная модель. метод наименьших квадратов. коэффициент детерминации.

модель парной линейной регрессии: y =  +*x +u (y- зависимая переменная,  +*x – неслучайная составляющая, х – независимая переменная, u- случайная составляющая)

Коэффициент детерминации.

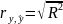
Метод наименьших квадратов: , S = , если S  min, то ,

4.Классическая нормальная модель линейной множественной регрессии.

5.Условия Гаусса – Маркова. Несмещенность коэффициентов регрессии. Точность коэффициентов регрессии. Теорема Гаусса – Маркова.

условия Гаусса-Маркова: 1. M(E_i)=0 – мат. ожидание случайного члена в любом испытании равно 0 2.D(E_i)=² – дисперсия случайного члена должна быть постоянная для всех наблюдений(условие гетероскедастичности). 3.M(E_i*E_j)=0, ij – отсутствие систематической связи м. значение случайного члена в 2х любых испытаниях. 4. M(x_i*E_i)=0 – Значение люб. независимой переменной должно считаться экзогенным, полностью определятся внешними причинами, не учитываемыми в уравнение регрессии.

Несмещенность коэффициента регрессии. на осн: м. доказать что b будет являться несмещенной оценкой β, если выполняется 4 усл. Гаусса-Маркова(M(x_i*E_i)=0)

β-const, т.к x – неслучайная величина, считаем что var(x) –величина известная, Cov(x,E)=0, получаем:

точность коэффициентов регрессии: ,

дисперсии a и b пропорциональны дисперсии остаточного члена 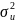. Чем больше фактор случайности, тем хуже будет оценка, при прочих равных условиях.

Теорема Гаусса-Маркова. если регрессионная модель y=b₀+b₁*x+E удовл. условиям Гаусса-Маркова, то оценки b₀ и b₁ имеют наименьшую дисперсию в классе всех несмещенных линейных оценок.

6.Определение доверительных интервалов для коэффициентов и функций регрессии. Доверительный интервал для параметров регрессионной модели.

коэффициент регрессии b и гипотетическое значение будут несовместимы, если выполняются условия : или ,т.е если величина удовл. двойному неравенству: (1). любое гипотетическое значение , кот, удовл. (1) будет автоматически совместимо с оценкой b. Множество всех этих значений , определенный как интервал между верхней и нижней границей неравенства наз. Доверительный интервал