Параграф 9: теоремы о пределах.

ТЕОРЕМА №1: (о единственности предела).

Если переменная имеет предел, то этот предел единственный.

Доказательство:

От противного: Предположим, что имеет различных пределов.

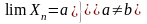
По лемме №1 о б.м. имеют места 2 равенства:

Вычтем почленно из одного неравенства другое:

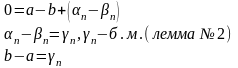
Это равенство противоречиво, т.к. с лева постоянное число неравное нулю, а справа, стремящаяся к нулю. Постоянное число не может стремиться к нулю. Противоречие доказывает теорему.

ТЕОРЕМА №2: (о предельном переходе в неравенстве.).

Пусть при всех n выполняется неравенство

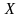
,и переменные и имеют пределы:

;

Тогда: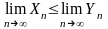 , т. е. .

Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.

Доказательство: (от противного)

Предположим, что

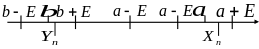
Выделим вокруг точек и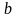 столь малые E – окрестности, чтобы они не пересекались.

По определению предела, начиная с некоторого номера n, переменные и попадут в свои E – окрестности предельных точек.

Это означает, что , начиная с некоторого номера n, что противоречит условию. Противоречие доказывает теорему, ч. т. д.

Замечание:

Если при всех n выполняется 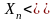(строго), то гарантировать строгого неравенства в пределе нельзя (в общем случае), гарантируется лишь нестрогое неравенство.

ПРИМЕР:

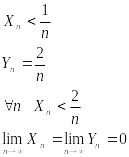
ТЕОРЕМА №3: (о стабилизации знака неравенства.).

Пусть предел и , тогда, начиная с некоторого номера n, переменная .

Доказательство:

Выберем столь малую E – окрестность точки , чтобы она целиком располагалась правее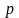 _. По определению предела, начиная с некоторого номера n, переменная попадает в E – окрестность точки _. Но это и означает, что для этих n:

Замечание:

Аналогично доказывается теорема о том, что если и , то, начиная с некоторого номера n, выполняется неравенство: .

ТЕОРЕМА №4: (арифметические операции над переменными, имеющими предел).

Пусть существуют пределы: и , тогда существуют пределы переменных:

1.

2.

3.

1.

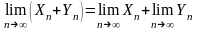
2.

3.

Доказательство:

Доказываем второй случай, остальные доказываются аналогично.

2 случай:

,

.

По Лемме №1 о бесконечно малых выполняется:

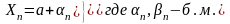
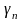– сумма трех переменных.

Переменная представилась в виде суммы: постоянной 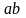и бесконечно малой , это и означает, что постоянная и есть предел этой переменной.

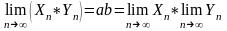, ч. т. д.

Эта теорема представляет другие возможности вычисления предела:

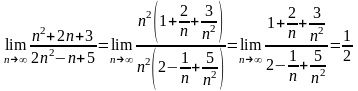
ТЕОРЕМА №5: (об ограниченности переменной, имеющей конечный предел).

Пусть переменная имеет конечный предел , тогда эта переменная является ограниченной переменной, что означает, что при всех n имеет место неравенство , где 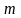и 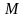– некоторые постоянные числа.

Доказательство:

Возьмем производную , по определению предела существует такой номер ,что при следует выполнение неравенства:

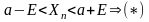
Значение переменной, которые могут не удовлетворять неравенство (*) лишь конечное число:

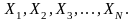
Рассмотрим множество чисел: 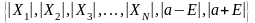выберем из них самое большое и обозначим 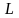, тогда при всех выполняется: 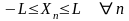, ч. т. д.

ТЕОРЕМА №6: (о сжатой переменной).

Пусть, начиная с некоторого , выполняются неравенства , причем крайние переменные имеют одинаковый конечный предел , тогда переменная также имеет предел, причем тот же самый.

Доказательство:

Возьмём любое , по определению предела начиная с некоторого номера будут выполняться неравенства:

и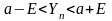

В силу неравенств (*) выполняется неравенство (начиная с некоторого номера ):

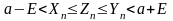
Это и означает, что переменная имеет пределом .

, ч. т. д.