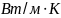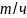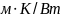2.3 Алгоритм расчета изменения температуры теплоносителя по длине аварийного (затопленного) участка теплотрассы

Вторая часть проблемы предусматривает расчет изменения температуры подающего и обратного теплоносителя по длине затопленной сети.

Для этого была разработана соответствующая математическая модель, представленная системой двух дифференциальных уравнений, связанных уравнением теплового баланса канала:

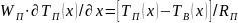; (2.11)

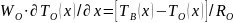; (2.12)

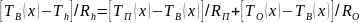; (2.13)

где 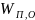– водяные эквиваленты соответственно подающего и обратного теплоносителя, ;

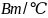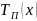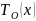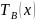, , – соответственно переменные по длине температуры теплоносителя в подающем и обратном трубопроводе и воды в канале, .

Отличительной особенностью данного случая от стандартной постановки задачи Коши является то, что начальные температуры подающего и обратного теплоносителя заданы на разных концах расчетного участка, т.е. имеет место противоток двух потоков (рис.2.2).

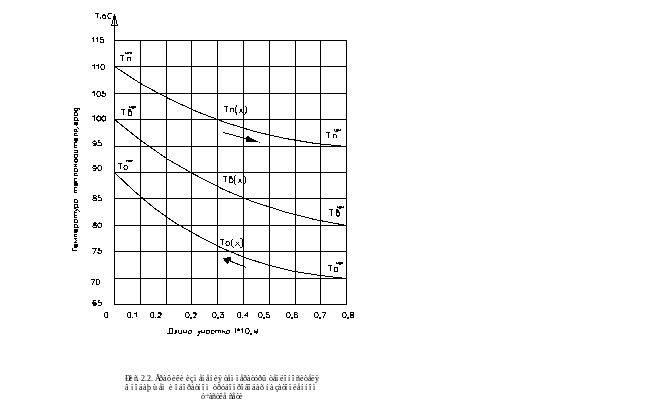
Поэтому предложен итерационный метод расчета. На одном из концов (слева), где известна начальная температура подающего теплоносителя, задается пробное значение температуры обратной воды. Методом Рунге-Кутта численно решается система дифференциальных уравнений, вычисляется температура обратного потока в конце расчетного участка (справа) и сравнивается с заданным значением. В случае их расхождения анализируется знак температурной невязки и ее величина, определенным образом корректируется новое значение температуры обратной воды (слева) и опять повторяется решение задачи Коши. При достаточно малом расхождении расчетной и заданной величины температуры обратной воды (справа) программа заканчивает свою работу, и на печать выводятся результаты.

2.4 Пример расчетов и анализ результатов

Приведем пример расчетов для следующих исходных данных.

Таблица 1 – Пример расчета

Параметр	Ед. измерения	Значение параметра по вариантам расчета
		1	2	3	4
Состояние канальной прокладки		Затоплена			Норма
Расчетный период года	час	5600	5600	5600	5600
Глубина заложения оси канала	м	1,5	1,5	1,5	1,5
Ширина канала	м	2	2	2	2
Высота канала	м	1	1	1	1
Теплопроводность грунта		1,4	1,4	1,4	1,4
Наружный диаметр труб теплосети	мм	300	300	300	300
Толщина теплоизоляции	мм	100	0,1	0,1	100
Теплопроводность теплоизоляции в нормативном состоянии		0,055	0,055	0,055	0,055
Температура стенки подающей трубы		110	110	110	110
Температура стенки обратной трубы		70	70	70	70
Длина затопленного участка	м	50	50	50	50
Расход подающего теплоносителя		40	40	100	40
Расход обратного теплоносителя		30	30	70	30

Таблица 2 – Результаты компьютерных расчетов по программе NADZOR1

Параметр	Ед. измерения	Значение параметра по вариантам расчета
		1	2	3	4
Температура на поверхности теплоизоляции подающего трубопровода		64,8	109,0	109,0	18,3
Температура на поверхности теплоизоляции обратного трубопровода		64,5	70,2	70,2	19,4
Температура воздуха (воды) в канале		64,2	89,4	89,4	14,4
Теплопотери подающего трубопровода		253,6	16245	16245	35,6
Теплопотери обратного трубопровода		114,4	-15740	-15740	50,7
Теплопотери всего канала		368,0	505	505	86,3
Термическое сопротивление теплоизоляции каждой трубы		0,137	0	0	1,478
Термическое сопротивление грунта и канала		0,18	0,18	0,18	0,18
Естественная температура грунта на уровне оси канала		-3,88	-3,88	-3,88	-3,88
Температура подающего теплоносителя в конце расчетного участка		109,7	92,54	103,0	109,9
Температура обратного теплоносителя в начале расчетного участка		69,84	92,56	79,67	69,93
Погрешность расчета		4*10-5	6*10-5	6*10-5	1*10-9

Результаты компьютерных расчетов рассматриваемой системы показывают, что теплопотери затопленного канала возрастают в 5-6 раз по сравнению с нормативными значениями.

Однако наиболее важным и неожиданным здесь является то, что теплопотери подающего трубопровода могут на порядок и более превышать свои нормативы.

Физически это объясняется тем, что затопленная канальная прокладка начинает работать как рекуперативный теплообменный аппарат. Температура воды в канале достигает достаточно высоких значений и становится выше температуры обратного теплоносителя. Таким образом, подающий трубопровод непроизвольно обогревает обратный, теплопотери которого принимают отрицательное значение.

Анализ проведенных расчетов также показывает, что в случае небольшой длины затопленного участка температуры подающего и обратного теплоносителя изменяются несущественно и анализ теплового режима канальной прокладки может быть ограничен только первой частью общей задачи. Для протяженных же участков при относительно малых расходах теплоносителя изменение температуры потоков может быть весьма ощутимым.

Таким образом, разработанная математическая модель и программа расчета теплового режима затопленных каналов могут обеспечить детальный анализ последствий аварийной ситуации и объяснить причины высокого значения температуры обратного теплоносителя, что довольно часто проявляется в спорах между поставщиком и потребителем тепловой энергии.

В заключение отметим, что разработанная компьютерная программа имеет достаточно важное практическое значение и передана для опытно-промышленного использования в ТУ «Красноярскгосэнергонадзор». Ниже, в качестве примера, приведена распечатка протокола работы разработанной компьютерной программы.