2.2 Алгоритм построения компьютерной программы. Основные расчетные зависимости определения теплопотерь

Для решения первых двух задач использован метод нелинейного математического программирования с составлением соответствующего функционала, представляющего собой тепловой баланс рассматриваемой системы.

В качестве неизвестных минимизируемого функционала приняты теплопотери подающей и обратной труб, а также температура воды в канале. Расчетные зависимости, входящие в построенный функционал, учитывают:

- процесс насыщения материала теплоизоляции водой;

- теплообмен между поверхностью теплоизоляции теплопроводов и внутренней средой в условиях естественной конвекции;

- кондуктивный теплоперенос из канала в окружающий массив грунта.

Теплопроводность теплоизоляции, насыщенной водой, принимается как эффективная, т.е. учитывает теплопроводность скелета материала и воды. В соответствии с работами [3,4,5] величина эффективной теплопроводности определяется по формуле:

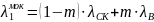; (2.1)

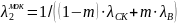; (2.2)

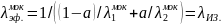, (2.3)

где – пористость материала [5];

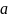– коэффициент, зависящий от пористости [5];

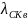– теплопроводность соответственно скелета материала и воды, 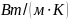[5,6].

Приведенные выше зависимости предусматривают две схемы стыковки различных сред (скелета и воды), как показано на рис.2.1.

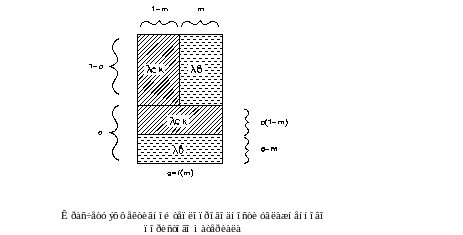
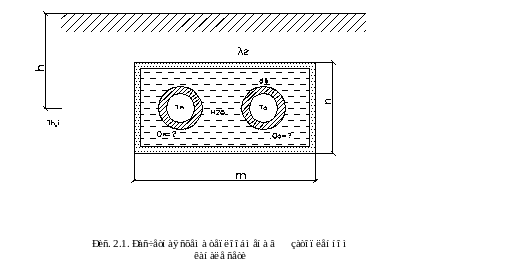
Теплообмен внутри канала между трубами и водой происходит в условиях естественной конвекции, поэтому для определения температуры на поверхности изоляции труб 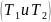введена следующая подстановка:

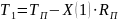; (2.4)

,

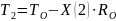где 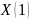, 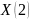– искомые теплопотери подающей и обратной труб, ;

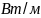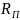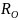, – термические сопротивления теплоизоляции подающей и обратной труб с учетом эффективной теплопроводности и внешнего сопротивления конвективному теплообмену на наружной поверхности, ,

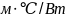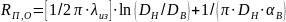, (2.5)

где 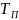, 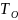– соответственно температуры теплоносителя внутри подающей и обратной труб, ;

.

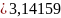Таким образом, температуры 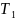и 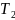еще не известны, но в общем виде они представлены через искомые мощности труб. Коэффициент конвективного теплообмена 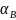является функцией критерия Рэлея:

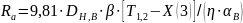, (2.6)

где 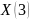– искомая температура воды в канале, ;

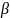– температурный коэффициент объемного расширения воды, 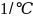[6];

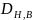– соответственно наружный и внутренний диаметр теплоизоляции (трубы), м;

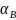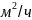– температуропроводность воды, [6];

– кинематическая вязкость воды, [6].

Искомый коэффициент конвективного теплообмена может быть определен по одной из формул, например, для 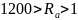[7]:

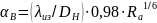. (2.7)

Таким образом, можно так построить алгоритм, чтобы на каждом шаге работы программы анализировалась величина критерия Рэлея и выбиралась соответствующая формула для вычисления коэффициента конвективного теплообмена. При этом возможно моделирование ситуации, когда теплоизоляция на трубах полностью разрушена, что можно сделать, задавшись весьма малым значением толщины последней.

Поиск искомых параметров 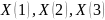ведется из условия минимума функционала, который представляет собой тепловой баланс канала:

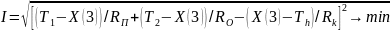, (2.8)

где 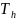– температура грунта на уровне заложения оси канала, [10];

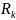– термическое сопротивление грунта, окружающего подземный канал теплосети, [11].

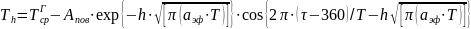, (2.9)

где 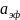= 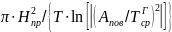– эффективная величина коэффициента температуропроводности грунта, учитывающая процесс фазового перехода грунтовой влаги в деятельном слое в течение года, [10];

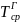– среднегодовая температура поверхности грунта, [8];

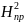– глубина сезонного промерзания грунта, м [8] ;

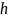– глубина заложения оси канала в грунт, м;

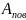– годовая амплитуда колебаний температуры наружного воздуха, [8];

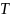– годовой период колебаний температуры наружного воздуха (8765 ч);

– расчетное время на момент проведения тепловых испытаний (отсчет ведется от 1 января текущего года), ч.

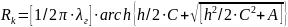, (2.10)

где ;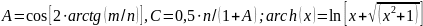

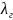– теплопроводность грунта, 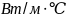[9];

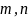– соответственно высота и ширина канала, м.

Многопараметрическая минимизация функционала осуществлялась численным методом Хука-Дживса по специально разработанной программе NADZOR1.