Electric field lines of force.

The direction of the electric field is always directed in the direction that a positive test charge would be pushed or pulled if placed in the space surrounding the source charge. Since electric field is a vector quantity, it can be represented by a vector arrow. For any given location, the arrows point in the direction of the electric field and their length is proportional to the strength of the electric field at that location. Such vector arrows are shown in the diagram below. Note that the lengths of the arrows are longer when closer to the source charge and shorter when further from the source charge.

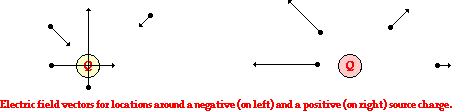
A more useful means of visually representing the vector nature of an electric field is through the use of electric field lines of force. Rather than draw countless vector arrows in the space surrounding a source charge, it is perhaps more useful to draw a pattern of several lines that extend between infinity and the source charge. These pattern of lines, sometimes referred to as electric field lines, point in the direction that a positive test charge would accelerate if placed upon the line. As such, the lines are directed away from positively charged source charges and toward negatively charged source charges. To communicate information about the direction of the field, each line must include an arrowhead that points in the appropriate direction. An electric field line pattern could include an infinite number of lines. Because drawing such large quantities of lines tends to decrease the readability of the patterns, the number of lines is usually limited. The presence of a few lines around a charge is typically sufficient to convey the nature of the electric field in the space surrounding the lines.

Principle or superposition.

The superposition theorem for electrical circuits states that for a linear system the response (Voltage or Current) in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, while all other independent sources are replaced by their internalimpedances.

To ascertain the contribution of each individual source, all of the other sources first must be "turned off" (set to zero) by:

Replacing all other independent voltage sources with a short circuit (thereby eliminating difference of potential. i.e. V=0, internal impedance of ideal voltage source is ZERO (short circuit)).
Replacing all other independent current sources with an open circuit (thereby eliminating current. i.e. I=0, internal impedance of ideal current source is infinite (open circuit).

Flux of a vector electric field intensity. Gauss theorem for electrostatic field.

In electromagnetism, electric flux is the flux of the electric field. Electric flux is proportional to the number of electric field lines going through a virtual surface. In other words the number of electric lines of force passing through the given surface area which is held perpendicular to the direction of electric lines of force is called electric flux. If the electric field is uniform, the electric flux passing through a surface of vector area S is

where E is the magnitude of the electric field (having units of V/m), S is the area of the surface, and θ is the angle between the electric field lines and the normal (perpendicular) to S. For a non-uniform electric field, the electric flux through a small surface area is given by

(the electric field, E, multiplied by the component of area perpendicular to the field). The electric flux over a surface S is therefore given by the surface integral: