moduli: 2. FML.
The Basic equations of molecular-kinetic theory of Gases.
The Kinetic theory gases of an equation is given as The Kinetic energy of the gas = (12) mv2 Where m is the mass of the gas molecule and v is the velocity of the gas. The kinetic energy of the gas is also given by the equationKinetic energy of the gas = (32) kT Where k is the Boltzmann constant and T is the temperature in K
Temperature.
All molecules of a gas do not possess the same speed, and this could be explained by the fact that during the collision of molecules, the speed or momentum changes. If initially the speed of a molecule is the same, it changes after the molecular collision. So it is seen that particles have different speeds, which are changing constantly. But although individual speed changes, the distribution of speed remains constant. That is the total velocity that does not change. But if the temperature of a gas is increased, then the average kinetic energy also changes.
Dependence of pressure on the molecules concentration and temperature.
Dependence on temperature and pressure
The Maxwell relation
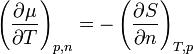
shows that the temperature variation of chemical potential depends on entropy. If entropy increases as the particle number increases, then chemical potential will decrease.
Similarly
shows that the pressure coefficient depends on volume. If volume increases with particle number, chemical potential also increases.
Boltsman's constant.
The Boltzmann constant (k or kB) is a physical constant relating energy at the individual particle level with temperature, which must necessarily be observed at the collective or bulk level. It is the gas constant R divided by the Avogadro constant NA:
It has the same dimension (energy divided by temperature) as entropy. It is named after the Austrian physicist Ludwig Boltzmann.
Avogadros number, molar mass.
In chemistry and physics, the Avogadro constant (symbols: L, NA) is defined as the number of constituent particles (usually atoms ormolecules) in one mole of a given substance. It is a dimensionless number and has the value 6.02214129(27)×1023 mol−1.[1][2][3] Changes in the SI units are proposed that will change the constant to exactly 6.02214X×1023 when it is expressed in the unit mol−1 (see New SI definitions).
In chemistry,
the molar
mass 
is
a physical property. It is defined as the mass of
a given substance (chemical
element or chemical
compound)
divided by its amount
of substance.[1] The
base SI
unit for
molar mass is kg/mol.
However, for historical reasons, molar masses are almost always
expressed in g/mol.
As an example, the molar mass of water is approximately: M(H2O) ≈ 18 g·mol−1
Ideal gas and its properties.
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.
An ideal gas has a number of properties; real gases often exhibit behavior very close to ideal. The properties of an ideal gas are:
An ideal gas consists of a large number of identical molecules.
The volume occupied by the molecules themselves is negligible compared to the volume occupied by the gas.
The molecules obey Newton's laws of motion, and they move in random motion.
The molecules experience forces only during collisions; any collisions are completely elastic, and take a negligible amount of time.