Это случай нулевых транзакционных издержек.

Х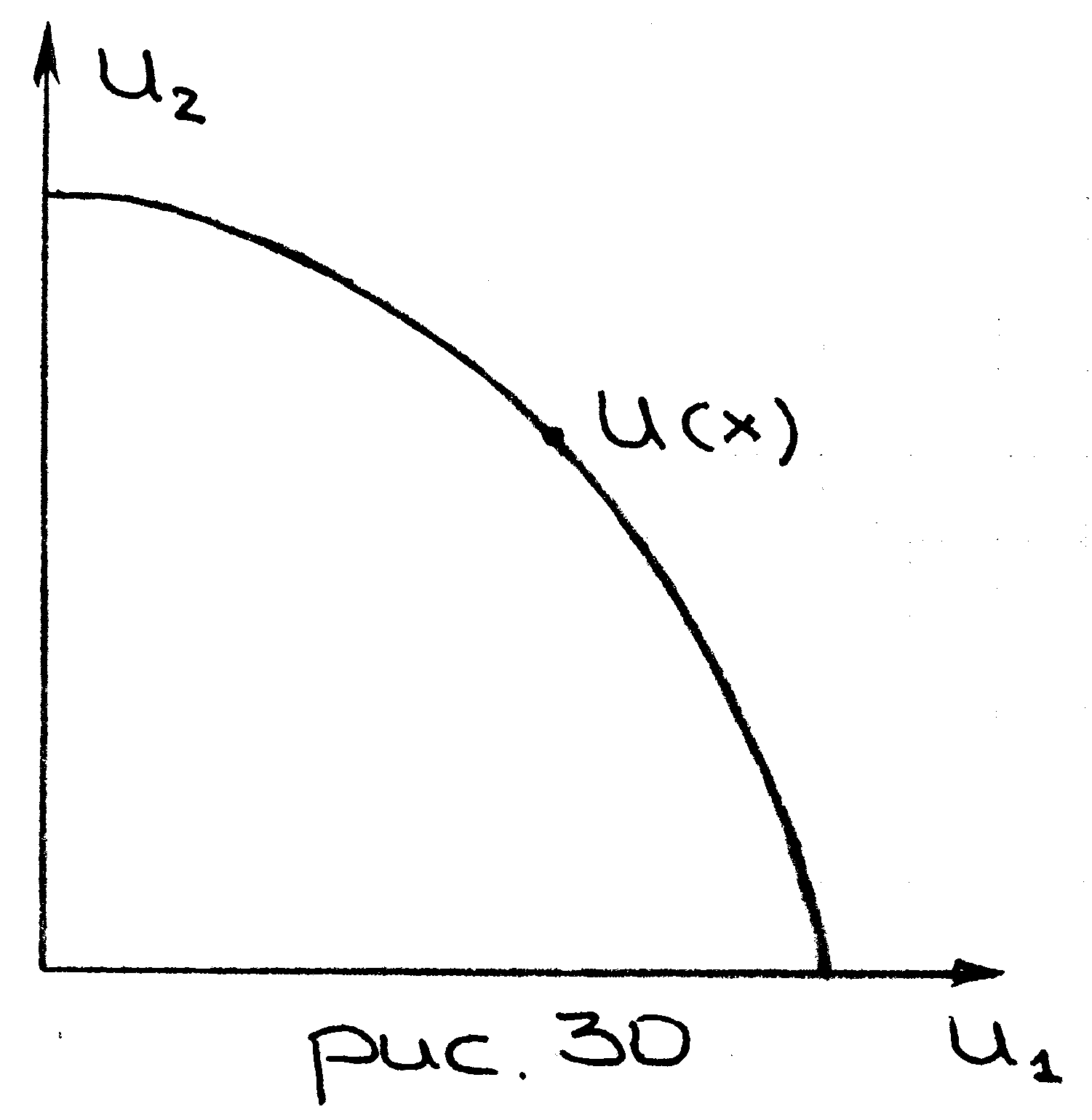 – количество товара, который распределяется между 2-мя участниками. Хотим сравнить распределение с изменением положения каждого участника. Можем построить спектр состояния, полученный путем перераспределения 1 количества Х.

где функции полезности максимизируются, уравнение после черты – процесс перераспре-деления. Нужно изобразить это множество.

в смысле Парето

участника

Понятие принципа компенсации

Распределение x’ потенциально эффективнее х: если можно перераспределить x’ таким образом, чтобы каждый эк. субъект предпочитал это новое распределение распределению х.

Определение: , если характеризующийся 2-мя свойствами:

1. Результат перераспределения

2. Улучшение по Парето

На рис. 32: , П – область Парето улучшения

X' потенциально эффективнее Х, т.к. такое, которое можно получить путем перераспределения X’ на первой кривой которая проходит через U(x’)

Принцип компенсации – такое улучшение состояния общества, при котором выигравшие способны более чем компенсировать ухудшение положения проигравших (в смысле Парето улучшения).

Кривая Калдера-Хикса (39г.) – существенно расширенная оценка состояния общества.

, если характеризующийся 2-мя свойствами:

- обеспечивает улучшение положения и 1-го и 2-го участника.

При переходе из x в x’ второй участник, не только с помощью перераспределения компенсирует потери 1-го, но и приводит к Парето улучшениям.

П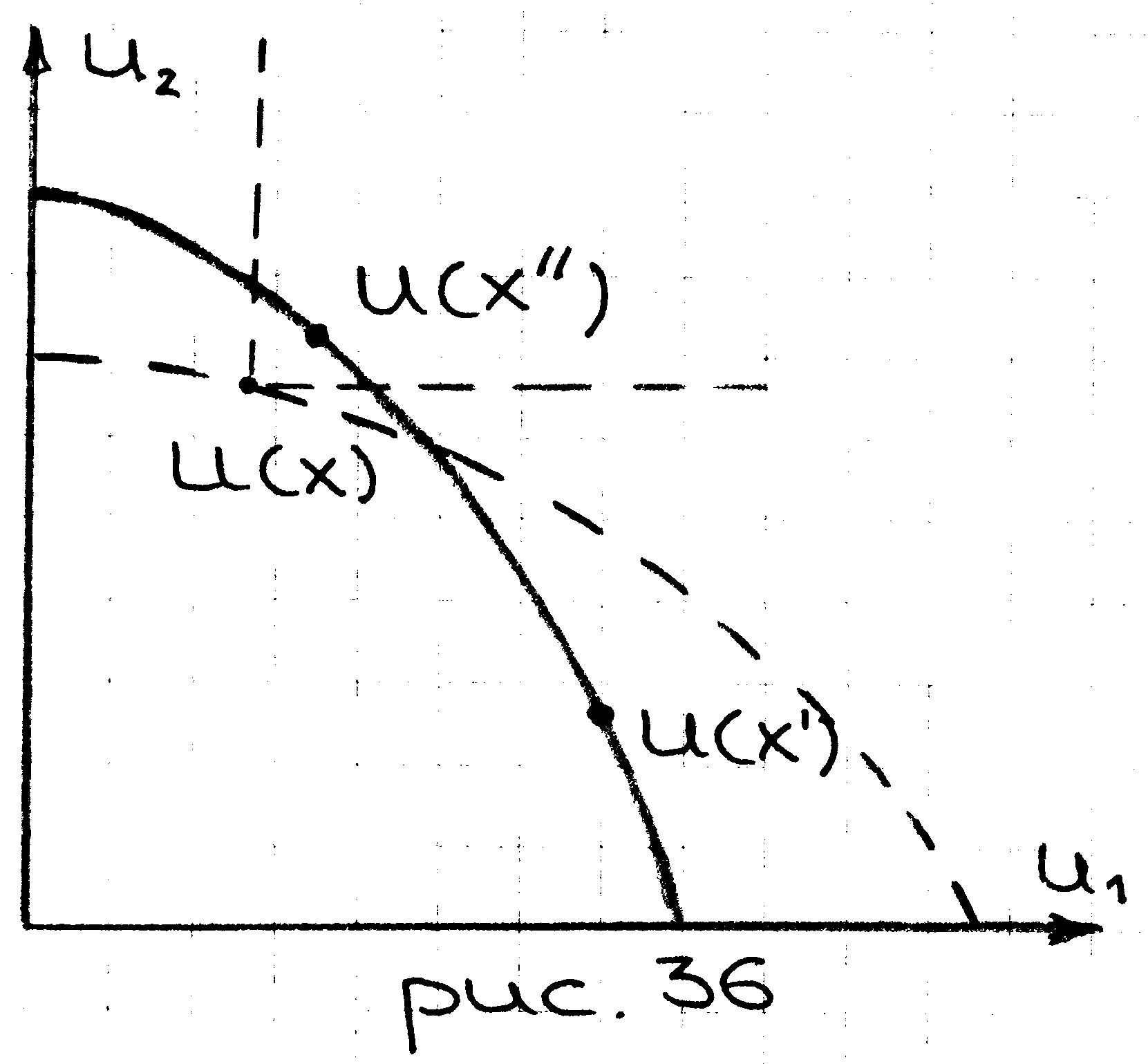 ринцип компенсации расширяет понятие Парето-оптимальности, но существует множество недостатков:

1. Принцип предусматривает возможность лишь потенциального, а не реального Парето – улучшения (реально выигравшие не обязательно будут компенсировать потери проигравших). Если бы реально можно было бы перейти к , то смысла в этом принципе нет (если можно и так из х в , то зачем x’)

2. Не позволяет сравнивать эффективные по Парето распределения лежащие на одной кривой возможных полезностей.

3. Предполагает созмерение выигрышей и потреь различных участников с единичными удельными весами (удельная полезность денег для разных участников предполагается одинаковой.

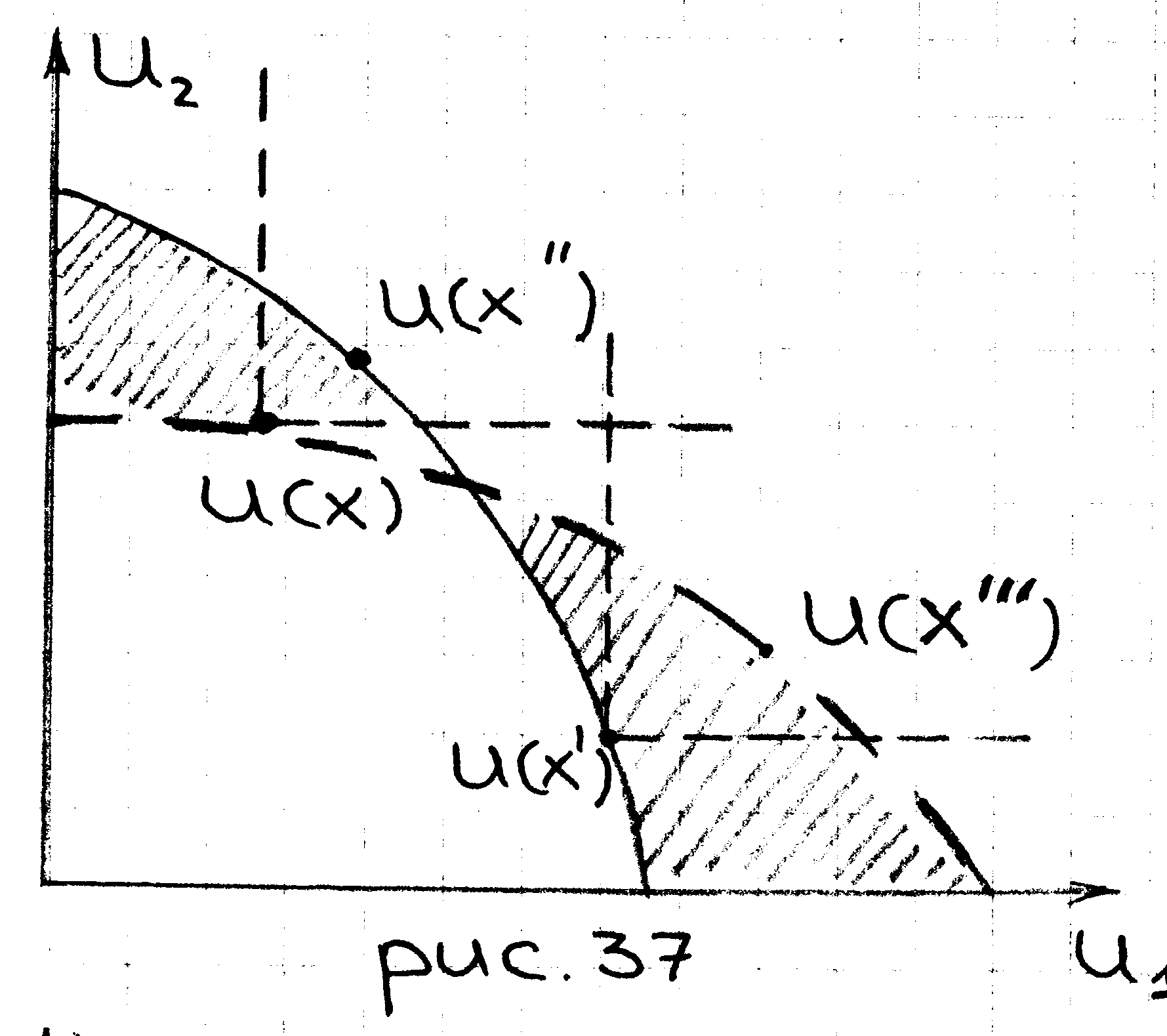4. П риводит к парадоксальным, противоречивым выводам:

Критерий роста национального дохода

Оценим состояние общества, используя цены.

Р – некоторый вектор цен. Х – состояние общества (х_i – потребительский набор i-го субъекта)

- величина национального дохода

Пусть экономика находится в состоянии рыночного равновесия – набор (Х,Р) – равновесный.

Если распределение , то переход их приводит к росту национального дохода, измеренного в текущих ценах.

где х – состояние конкурентного равновесия  (наилучшая рх_i среди любых других)

- рост национального дохода

П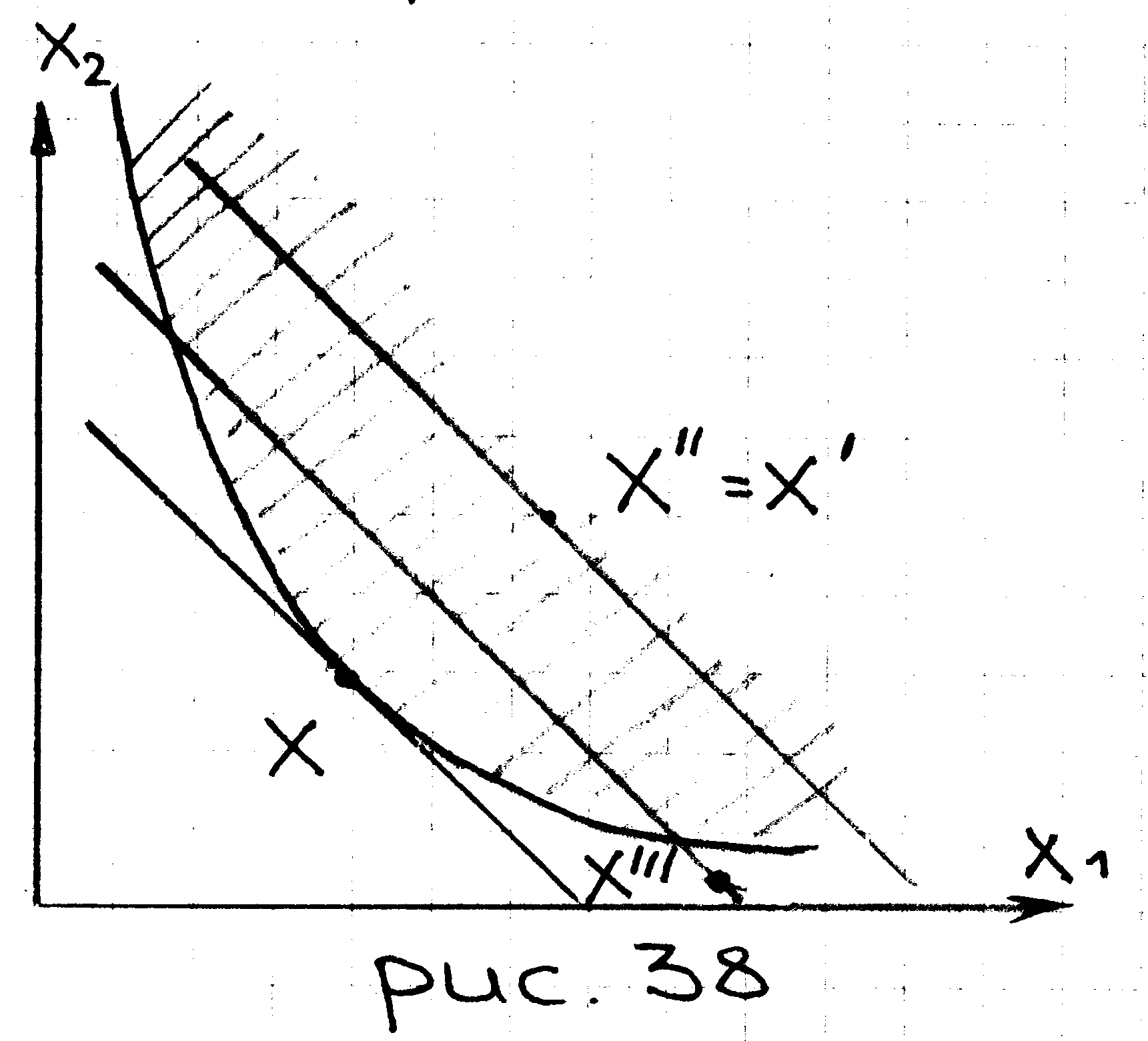 роиллюстрируем на примере:

группы товаров

- множество потенциально эффективных состояний экономики (совпадает с Парето-опт.)

• линия цен касается (т.к. состояние х – равновесное)

Обратное утверждение неверно. Национальный доход при больше чем при x’ но не является потенциально эффективным

Для принятия решения государству нужно использовать межличностные оценки.