12. Уравнения для токов в сечениях цепи. Матрица сечений.

Ранее мы выяснили, что число независимых уравнений, согласно первому закону Кирхгофа, равно q – 1. Следовательно, число независимых уравнений для сечений также должно быть равно q – 1, так как каждое уравнение для сечения может быть получено суммированием соответствующих узловых уравнений для узлов, охваченных сечением. Чтобы упростить выбор сечений, целесообразно проводить их таким образом, чтобы каждое сечение разрезало только одну ветвь дерева. При этом число сечений будет равно числу ветвей дерева. Условимся нумеровать сечения номерами ветвей дерева. Условимся также термин направление ветви применять в качестве синонима термина направление тока в ветви. Направим нормаль к поверхности сечения внутрь или наружу в зависимости отнаправления ветви дерева. Тогда в уравнение для токов в сечении ток ветви дерева и токи ветвей, ориентированные по отношению к сечению так же, как и ток ветви дерева, войдут со знаком «плюс». Все остальные токи войдут в уравнение со знаком «минус». Токи ветвей, не разрезаемых сечением, не войдут в уравнение. Учтем это обстоятельство в записи уравнений введением коэффициентов d_mk, где m — номер ветви дерева, определяющий номер сечения; k — номер ветви. Причем d_mk = ±1, если k-я ветвь разрезается m-м сечением, и d_mk = 0, если k-я ветвь не входит в m-е сечение. Тогда уравнение для токов сечений можно записать в виде Прямоугольная матрица, строки которой соответствуют ветвям дерева, а столбцы — ветвям направленного графа электрической схемы, элементы которой равны нулю, единице, минус единице, если при образовании замкнутой поверхности, разрезающей только одну ветвь дерева и связи графа, ветвь, соответственно, не разрезается, разрезается и направлена к поверхности согласно данной ветви дерева, разрезается и направлена к поверхности против данной ветви графа, называется матрицей сечений. Каждая строка матрицы сечений представляет собой коэффициенты у токов ветвей в уравнении для сечения, номер которого определяется номером ветви дерева. 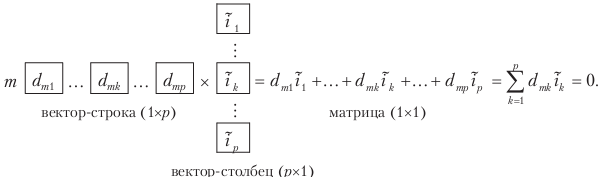Согласно правилам матричного умножения, каждое уравнение сечения может быть записано в виде Такие матричные уравнения можно записать для всех q – 1 ветвей дерева графа схемы. 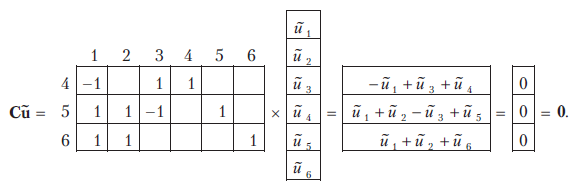В матричной форме полученную систему уравнений можно представить в виде Для графа схемы имеем

1 1. Контурные уравнения цепи. Матрица контуров.

Применяя второй закон Кирхгофа, можно составить столько уравнений, сколько имеется контуров в цепи(одни уравнения могут оказатьсяследствиями других). Независимость контуров, будет обеспечена, если эти контуры выбирать так, чтобы каждый последующий отличался от предыдущих, как минимум, однойновой ветвью.Проще сделать этот выбор, если воспользоваться свойствами дерева графа, которое представляет собой такую совокупность ветвей, которая не образует контуров. Добавление любой связи графа схемы создает контур, который образуется одной связью и ветвями дерева графасхемы. 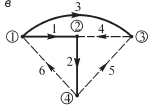Добавление связи 5 образует контур 5, куда входят ветви дерева 1, 2 и 3.(рис.6).число независимых контуров определяется числом связей в каждом связном графе схемы, т. е. n=p – (q – 1). Запишем контурные уравнения для графа схемы. Обозначим напряжения ветвей графа схемы через u(индекс-k). Контурные уравнения пронумеруем согласно номерам ветвей-связей. Обход контура произведем таким образом, чтобы направление связи совпало с направлением обхода. В контурное уравнение напряжение ветви войдет со знаком «плюс», если направления обхода и стрелки ветви совпадают, в противном случае напряжение войдет со знаком минус. Учтем это обстоятельство в записи уравнений введением коэффициентов С(индекс-sk), где Sномер связи, k-номер ветви. С(sk)=1если k-я ветвь входит в s-й контур против обхода; С(sk)=0если k-я ветвь не входит в s-й контур.При таком подходе второй закон Кирхгофа для графа схемы можно записать в виде: . Для нашего контура имеем: Составим таблицу из коэффициентов С(sk). Пронумеруем строки этой таблицы номерами связей графа цепи, а столбцы — номерами ветвей графа цепи. Такую прямоугольную матрицу, строки которой соответствуют связям, а столбцы —ветвям направленного графа электрической схемы, элементы которой равны нулю, единице или минус единице, если при обходе контура, образованного данной связью и ветвями дерева, вдоль связи ветвь, соответственно, не входит в контур, входит в контур согласно обходу, входит в контур против обхода, называют матрицей контуров.Обозначим матрицу контуров буквой С.Представим напряжения ветвей графа схемы в виде матрицы, состоящей из р строк и одного столбца: Каждая строка матрицы контуров представляет собой коэффициенты у напряжений ветвей графа в уравнении, записанном согласно второму закону Кирхгофа для контура, который образован связью, номер которой определяет номер строки матрицы контуров. Таким образом, согласно правилам матричного умножения, каждое контурное уравнение может быть записано в виде: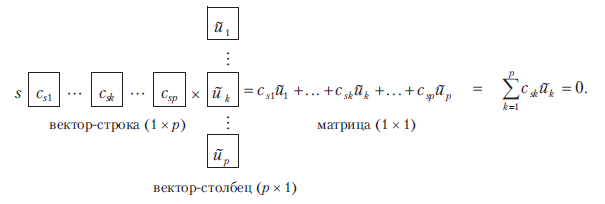

Такие матричные уравнения можем записать для всех п связей графа схемы. В матричной форме полученную в итоге систему уравнений можно представитьв виде: С*u=0.

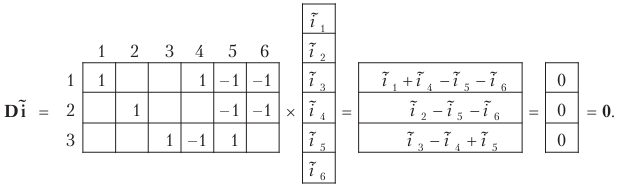
Для такого графа имеем: