10. Схемы электрических цепей. Топологические понятия схемы электрической цепи. Граф схемы. Законы электрических цепей

Для расчета процессов в электрической цепи следует определить математические соотношения для отдельных участков исходной цепи, по этим соотношениям построить некую другую цепь, анализ процессов в которой заменит анализ процессов в исходной реальной цепи. Схему этой другой электрической цепи, отображающей при определенных условиях свойства реальной цепи, называют с х е м о й з а м е щ е н и я э л е к т р и ч е с к о й ц е п и или кратко — с х е м о й з а м е щ е н и я. Электрическая цепь и, соответственно, ее схема имеют в общем случае в е т в и и у з л ы. Ветвью электрической цепи и, соответственно, ее схемы называют весь участок электрической цепи, в котором в любой момент времени ток имеет одно и то же значение вдоль всего участка. Ветвь может содержать любое число последовательно соединенных элементов цепи: участков с сопротивлением, конденсаторов, индуктивных катушек, источников ЭДС. При этом последовательным соединением участков электрической цепи называют соединение, при котором через все участки цепи проходит один и тот же ток. Узлом электрической цепи и, соответственно, ее схемы называют место соединения ветвей. На схеме узел изображают точкой. Параллельным соединением участков (ветвей) электрической цепи называют соединение, при котором все участки (ветви) цепи присоединяются к одной паре узлов и на всех этих участках (ветвях) имеется одно и то же напряжение. Смешанным соединением участков электрической цепи называют сочетание последовательного и параллельного соединений. Электрическую цепь называют п л о с к о й (п л а н а р н о й), если она может быть изображена на плоскости в виде схемы с непересекающимися ветвями. Контуром электрической цепи называют любой замкнутый путь, проходящий по нескольким ветвям. Любая часть электрической цепи, имеющая два зажима (полюса), называется двухполюсником. Активным называют двухполюсник, содержащий источники электрической энергии. Для линейного двухполюсника обязательным дополнительным условием является наличие на его разомкнутых зажимах напряжения, обусловленного источниками электрической энергии внутри двухполюсника, т. е. необходимо, чтобы действия этих источников энергии не компенсировались взаимно внутри двухполюсника. Пассивным называют двухполюсник, не содержащий источников электрической энергии. Линейный двухполюсник может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых зажимах равно нулю. Чтобы сделать более наглядным изображение взаимных соединений ветвей схемы, целесообразно ввести в рассмотрение такое изображение схемы электрической цепи, в котором ветви схемы представлены отрезками — ветвями графа, а узлы — точками — узлами графа. Такое топологическое представление схемы электрической цепи носит название г р а ф а э л е к т р и ч е с к о й с х е м ы или короче — гр афасхемы. Граф, между любой парой узлов которого имеется ветвь или совокупность ветвей, называют св я з н ы м. Если на графе имеется указание условно-положительных направлений токов или напряжений в виде отрезков со стрелками, то такой граф называют н а п р а в л е н н ы м г р а ф о м с х е м ы. Важным топологическим понятием графа схемы является д е р е в о г р а ф а с х е м ы, представляющее собой любую совокупность ветвей графа, соединяющих все узлы графа без образования контуров. Один и тот же граф схемы может иметь различные деревья. Ветви, дополняющие дерево графа до полного графа и, следовательно, не принадлежащие дереву графа, принято называть с в я з я м и г р а ф а с х е м ы. Если связный граф имеет p ветвей и q узлов, то в его дереве будет q – 1 ветвей, а число связей окажется равным n = p – (q – 1) Например, 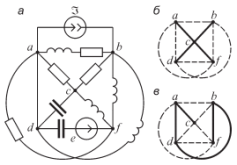p = 10, q = 5 и n = 6. Первый закон Кирхгофа - т. е. сумма токов, расходящихся от узла электрической цепи, равна нулю. Второй закон Кирхгофа - сумма падений напряжения во всех ветвях любого замкнутого контура электрической цепи равна сумме ЭДС источников энергии, действующих в этом контуре - .