Источники эдс и источники тока

Источники энергии в электрических цепях принято рассматривать как источ­ники ЭДС или как источники тока. К источникам ЭДС обычно относят источники электромагнитной энергии, в которых ЭДС e не зависит или практи­чески не зависит от тока, идущего от источника в приемник, и внутреннее сопро­тивление г_вн которых мало, так что напряжение u = e – ir_вн на зажимах источника сравнительно мало изменяется в пределах изменения тока от нуля до номинального i_ном.

Линейная цепь должна содержать только ис­точники ЭДС с линейной характеристикой. Если r_вн=0 и е = const, то и = е = const, и такой источник будем называть иде­альным источником ЭДС. Если у реального источника, имеющего r_вн ≠0, условно вынести его внутреннее сопротивление, то получим условное изображение источника ЭДС:

Необходимо указать стрелкой положительное направление ЭДС е. В общем случае это есть условное положительное направление ЭДС, так как ЭДС может быть перемен­ной, например периодической, величиной. Если теперь отнести r_вн к приемнику, добавив его к

с опротивлению приемника, то цепь будет рассматри­ваться как содержащая идеальный

источник ЭДС:

В случае когда характеристика и = f(i) криволинейна цепь, содержащая такой источник,

является нелинейной цепью.

Источниками линейной ЭДС являются, например, аккумуляторы, гальвани­ческие элементы,

вращающиеся электрические генераторы постоянного тока.

К источникам тока обычно относят источни­ки электромагнитной энергии, в которых ток не зависит или практически не за­висит от напряжения и, которое создается источником на зажимах приемника. Заданный ток источника тока обозначают буквой J. Предполагается, что источник тока имеет достаточно малую внутреннюю проводимость g_вн, так что ток i = J – u*g_вн, поступающий в приемник, мало изменяется в пределах изменения напряжения и от нуля до номинального и_ном. Характеристика идеального источника тока: J = const и g_вн = 0, при котором i=J= const.

Если условно вынести проводимость g_вн, то получим условное

изображение источника тока

Необходимо указать стрелкой условное положительное направление тока 3. Если отнести проводимость g_вн к приемнику, добавив ее к

проводимости g_пр приемника, то цепь бу­дет

рассматриваться как содержащая идеальный источник тока:

Линейными источника­ми тока являются, например, источники энергии, основан­ные на излучении заряженных частиц, выделяющихся при радиоактивном рас­паде вещества.

Важными разновидностями источников ЭДС и тока являются зависимый ис­точник ЭДС и зависимый источник тока. Зависимым источником электродвижущей силы называют такой источник, в котором ЭДС зави­сит от тока или напряжения в некотором участке цепи. Аналогично источник тока, в котором ток зависит от тока или напряжения в некотором участке цепи, называют зависимым источником тока.

4 Типа зависимых источников: а)инун: б)инут: в)итун: г)итут:

Примером зависимого источника может служить операционный усилитель, в котором входной и выходной величинами являются напряжения u_ab и u_cd:

В случае, когда полярности напряжений на входе и вы­ходе усилителя противоположны, коэффициент усиления принимается рав­ным —k, и такой усилитель называют инвертирующим.

Схемы электрических цепей. Топологические понятия схемы электрической цепи. Граф схемы. Законы электрических цепей Электрическую цепь на чертежах изображают в виде схемы, под которой пони­мают графическое изображение электрической цепи, содержащее условные обо­значения ее элементов и показывающее соединения этих элементов. Записанные в аналитической форме соотношения между величинами элемента электрической цепи являются математической моделью этого элемента. математическим соотношениям могут быть поставлены в соответствие электрические цепи, содержащие идеальные индук­тивные катушки и резисторы. Математическим соотношениям между величинами могут быть поставле­ны в соответствие электрические цепи, содержащие только идеализированные элементы .Очевидно, схемы таких цепей и сами цепи тождественны..Для расчета процессов в электрической цепи следует опреде­лить математические соотношения для отдельных участков исходной цепи, по этим соотношениям построить некую другую цепь, анализ процессов в которой заменит анализ процессов в исходной реальной цепи. Схему этой другой электрической цепи, отображающей при определенных условиях свойства реальной цепи, называют схемой замещения.

Электрическая цепь и, соответственно, ее схема имеют в общем случае вет­ви и узлы.

Ветвью электрической цепи и, соответственно, ее схемы называют весь уча­сток электрической цепи, в котором в любой момент времени ток имеет одно и то же значение вдоль всего участка.

Ветвь может содержать любое число последовательно соединенных элемен­тов цепи. При этом последовательным соединением участков электриче­ской цепи называют соединение, при котором через все участки цепи проходит один и тот же ток.

Узлом электрической цепи и, соответственно, ее схемы называют место со­единения ветвей. Параллельным соединением участков (ветвей) электрической цепи называют соединение, при котором все участки (ветви) цепи присоединяются к одной паре узлов и на всех этих участках (ветвях) имеется одно и то же напряжение

Смешанным соединением участков электрической цепи называют сочетание последовательного и параллельного соединений.

Электрическую цепь называют плоской ,если она может быть изображена на плоскости в виде схемы с непересекающимися ветвями. Контуром электрической цепи называют любой замкнутый путь, проходящий по нескольким ветвям.

В электрических схемах цепи или в схемах замещения узлы изображаются точ­ками. В сложных схемах, где возможны взаимные пересечения линий, изобра­жающих соединительные провода, для обозначения существования их электри­ческих соединений также используются точки.

Чтобы сделать более наглядным изображение взаимных соединений ветвей схемы, целесообразно ввести в рассмотрение такое изображение схемы электри­ческой цепи, в котором ветви схемы представлены отрезками — ветвями графа, а узлы — точками — узлами графа. Такое топологическое представление схемы электрической цепи носит название графа электрической схемы или короче — графа схемы. На топологической схеме источники ЭДС и тока не изобража­ются. При этом ветвь с источником ЭДС сохраняется. Ветви же с идеальными источниками тока вообще не входят в топологическую схему.

Важным топологическим понятием графа схемы является дерево графа схемы, представляющее собой любую совокупность ветвей графа, соединяю­щих все узлы графа без образования контуров. Один и тот же граф схемы может иметь различные деревья. Условимся ветви графа схемы, образующие дерево, изображать жирными линиями.

Ветви, дополняющие дерево графа до полного графа и, следовательно, не при­надлежащие дереву графа, принято называть связями графа схемы. Изображают пунктиром.

При расчете электрических цепей используются два закона Кирхгофа. Первый закон Кирхгофа, или закон Кирхгофа для узлов, применительно к уз­лам электрической цепи вытекает из принципа непрерывности электрического тока и формулируется: сумма токов, расходящихся от узла электрической цепи, равна нулю. Второй закон Кирхгофа, или закон Кирхгофа для контуров, применяется к контурам электрической цепи. Гласит: сумма падений напряжения во всех вет­вях любого замкнутого контура электрической цепи равна сумме ЭДС источни­ков энергии, действующих в этом контуре.

Уравнения согласно законам Кирхгофа для графа схемы:

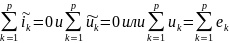
Контурные уравнения цепи. Матрица контуров Независимость контуров, будет обеспечена, если эти контуры выбирать так, что­бы каждый последующий отличался от предыдущих, по крайней мере, одной новой ветвью. Наиболее просто такой выбор можно осуществить, если восполь­зоваться свойствами дерева графа, которое представляет собой такую совокуп­ность ветвей, которая не образует контуров. Добавление любой связи графа схе­мы создает контур, который образуется одной связью и ветвями дерева графа схемы. Число независимых контуров определяется числом связей в каждом связном графе схемы.

З апишем контурные уравнения для графа схемы. Обозначим напряжения ветвей графа схемы через 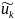.Контурные уравнения пронумеруем согласно номерам ветвей-связей. Обход контура произведем таким образом, чтобы направление связи совпало с направлением обхода. В контурное уравнение напряжение ветви войдет со знаком «плюс», если направления обхода и стрелки ветви совпадают, в противном случае напряжение войдет со знаком минус. Учтем это обстоятель­ство в записи уравнений введением коэффициентов с_sk, где s — номер связи; k — номер ветви. Будем считать, что с_sk = 1, если k-я ветвь входит в s-й контур соглас­но его обходу; с_sk = -1, если k-я ветвь входит в s-й контур против обхода; с_sk = 0, если

k-я ветвь не входит в s-й контур. При таком подходе второй закон Кирхгофа для графа схемы можно записать в виде

Составим таблицу из коэффициентов c_sk. Пронумеруем строки этой таблицы номерами связей графа цепи, а столбцы — номерами ветвей графа цепи. Такую прямоугольную матрицу, строки которой соответствуют связям, а столбцы — ветвям направленного графа электрической схемы, элементы которой равны нулю, единице или минус единице, если при обходе контура, образованного данной связью и ветвями дерева, вдоль связи ветвь, соответственно, не входит в контур, входит в контур согласно обходу, входит в контур против обхода, называют матрицей контуров.

Обозначим матрицу контуров буквой С.

Матричные уравнения можем записать для всех п связей графа схемы. В матричной форме полученную в итоге систему уравнений можно представить в виде: С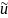 =0.

Матричная запись контурных уравнений для напряжений и ЭДС в ветвях схемы будет иметь вид:

Cu = Cu - Ce = 0,