Приклад розрахунку

Розрахувати струми у вітках електричного кола, зображеного на рисунку 1.3, методом контурних струмів.

Дане коло нараховує три незалежні контури: badb; acda; bcab.

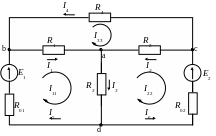
Рисунок 1.5 – До розрахунку електричного кола методом контурних струмів

Черговість розрахунку

1 Задаються умовно-додатними напрямами контурних струмів , , (рисунок 1.5);

2 Складають для незалежних контурів рівняння за другим законом Кірхгофа:

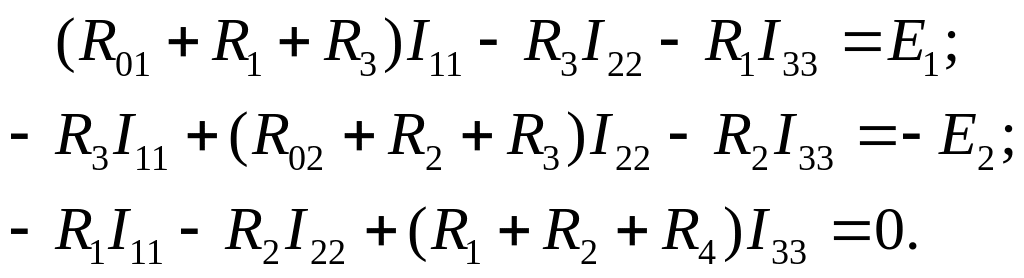
3 Розрахувавши одержану систему рівнянь, визначають контурні струми , , .

4 Реальні значення струмів у зовнішніх вітках електричного кола дорівнюють модулям відповідних контурних струмів, а в суміжних вітках визначаються як алгебрична сума відповідних контурних струмів.

Підставивши в рівняння числові значення ЕРС та опорів резисторів, одержимо:

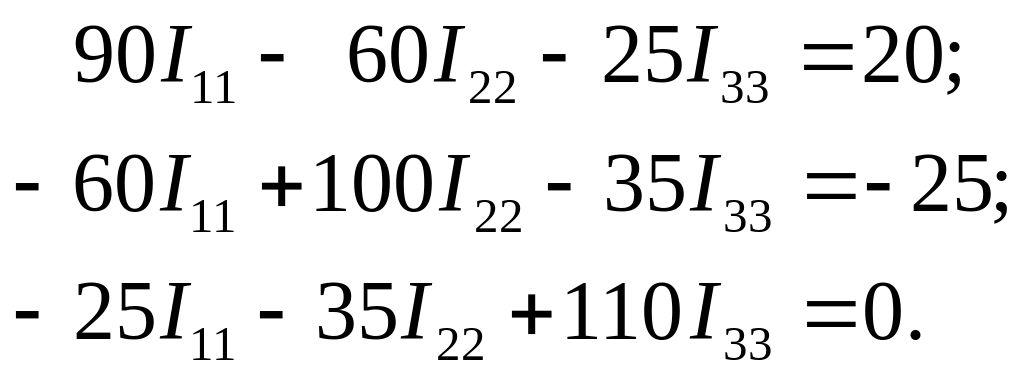
Після виконання розрахунків одержимо такі значення контурних струмів:

А; А; А.

5 Позначивши умовно-додатні напрями струмів у вітках схеми, знаходимо їх як алгебраїчну суму контурних струмів, що протікає через дану вітку.

Значення струмів у вітках визначають через контурні струми:

А,

А,

А,

А,

А,

А.

1.2.3 Метод еквівалентного генератора

Якщо необхідно розрахувати струм тільки в одній вітці складного електричного кола, то доцільно застосовувати метод еквівалентного генератора. У даному методі дію всіх джерел складного електричного кола на досліджувану вітку замінюють дією еквівалентної ЕРС _, з внутрішнім опором _.

Черговість розрахунку

1 Вибирають умовно-додатний напрям струму в досліджуваній вітці.

2 Розмикають досліджувану вітку, здійснюючи режим неробочого ходу.

3 Визначають напругу неробочого ходу на затискачах розімкненої вітки, вибравши напрям дії напруги проти напряму струму. При цьому .

4 Знаходять еквівалентний опір кола відносно розімкненої вітки, вилучивши із схеми всі джерела ЕРС.

5 Струм в k - ій досліджуваній вітці визначають за формулою

,

де – ЕРС джерела, що діє в досліджуваній вітці; – опір досліджуваної вітки.

Знаки плюс чи мінус вибирають у відповідності за законом Ома для вітки з джерелом. Якщо напрям ЕРС співпадає з напрямом струму, то беруть знак ”плюс”, в іншому випадку – “мінус”.

Приклад розрахунку

Розрахувати методом еквівалентного генератора струм у вітці з резистором для розрахункової схеми, наведеної на рисунку 1.3, який дорівнює:

.

Розраховуємо напругу неробочого ходу на затискачах вітки (рисунок 1.6)

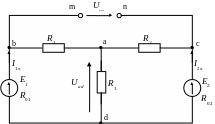
Рисунок 1.6 – Схема для розрахунку струму у вітці nm

Складаємо рівняння для контура ndmn за другим законом Кірхгофа

,

звідки

.

Для розрахунку струмів та визначимо вузлову напругу

.

Тоді

А,

А,

В.

Визначимо еквівалентний опір відносно затискачів , вилучивши із схеми ЕРС . Схема прийме вигляд, показаний на рисунку 1.7.

Перетворимо схему зєднання опорів , , трикутником в еквівалентну зірку (рисунок 1.7). Схема набуде вигляду (рисунок 1.8).

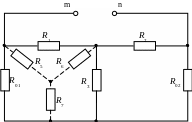
Рисунок 1.7 – Визначення еквівалентного опору

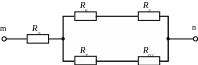
Рисунок 1.8 – Перетворена схема

При цьому еквівалентний опір дорівнює:

,

де ; ; .

Підставивши значення ( ) та , одержимо

.