Связь силы с потенциальной энергией
С одной стороны работа равна:
(25)
С другой стороны работа равна:
(26)
Тогда
(27)
(28)
Таким образом,
;
;
(29)
или
,
(30)
где выражение
(31)
называется оператором Гамильтона.
Таким образом:
(32)
(33)
- вектор силы, действующий на частицу равен градиенту потенциальной энергии и направлен в сторону убывания потенциальной энергии.
Потенциальная энергия упруго-деформированного тела
Р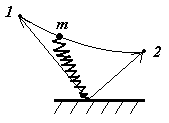
аботу
силы упругости можно найти по формуле:
(34)
Если сила упругости
равна:
,
(35)
где x – смещение.
Тогда работа силы упругости равна:
(36)
(37)
потенциальная
энергия упруго-деформированного тела
(38)
Потенциальная энергия поля тяготения
(39)
(40)
Тогда
(41)
потенциальная
энергия поля тяготения (42)
Закон сохранения энергии (зсэ)
закон сохранения механической энергии: в замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т.е. не изменяется со временем
В замкнутой системе, в которой действуют силы трения, полная механическая энергия системы при движении убывает. Следовательно, в таких случаях ЗСЭ несправедлив. Однако при исчезновении механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается сущность ЗС и превращения энергии – сущность неуничтожимости материи и ее движения.
Скорости тел при центральном ударе.
Упругий и неупругий удар
Удар (или соударение) – это встреча двух или более тел, при котором взаимодействие длится очень короткое время. Примером соударений могут быть столкновение биллиардных шаров или столкновение летящей пули с мешком песка и т.д. При ударе в телах возникают внутренние силы, однако этими силами можно пренебречь в виду их незначительности. И это упрощение позволяет соударяющиеся тела рассматривать как замкнутую систему и применять к ней законы сохранения.
Различают центральные и нецентральные удары. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через центы их масс.
Удары так же могут быть абсолютно упругими и неупругими.
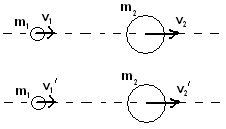АУУ
называют столкновение двух тел, в
результате в обоих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию.
В данном случае направление движения первого тела будем считать положительным, второго – отрицательным.
Если
и
- масса и скорость первого тела до удара;
и
- масса и скорость второго тела до удара,
а
и
- скорости тел после удара, законы
сохранения будут иметь вид:
и
.
Откуда выражаем и :
,
.
АНУ называют столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Д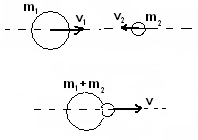
ля
АНУ закон сохранения количества движения
будет иметь вид:
,
откуда скорость движения сцепки:
.
Скорости тел при абсолютно упругом ударе.
и
.
После преобразований этих выражений получим:
,
,
Откуда
.
Решая уравнения, получаем:
, .
Частные случаи для АУУ:
1) при
,
а) при
.
Если второй шар до удара висел неподвижно
(
),
то после удара остановится первый шар
(
),
а второй будет двигаться с той же
скоростью и в том же направлении, в каком
двигался первый шар до удара (
).
б)
.
Первый шар продолжает двигаться в том
же направлении , как и до удара, но с
меньшей скоростью (
).
Скорость второго шара после удара
больше, чем скорость первого после удара
.
в)
.
Направление движения первого шара при
ударе изменяется – шар отскакивает
обратно. Второй шар движется в ту же
скоростью, в какую двигался первый шар
до удара, но с меньшей скоростью.
г)
(например, столкновение со стеной). Из
уравнений (а)) следует, что
,
.
2) при
.
Уравнения из (а) будут иметь вид:
,
,
т.е. шары равной массы обменяются
скоростями.