2. Квантовое число как результат решения уравнения Шредингера
Приближённая картина движения электрона в поле ядра по Бору нуждалась в существенном изменении. В модели Бора электрон движется по круговой орбите и обладает одной степенью свободы. На самом деле электрон, вращаясь вокруг ядра, имеет 3 степени свободы, поэтому функция, описывающая это движение, является функцией 3-х координат:
.
Воспользуемся уравнением Шредингера для пространственной системы координат:
.
Для его решения удобно использовать сферическую систему координат:
,
где:
.
Результат решения этого уравнения имеет вид:
.
Этот результат
определяется тремя квантовыми числами:
n
– главным;
– орбитальным (азимутным) и m
– магнитным.
1) Главное квантовое число n – определяет энергетические уровни электрона в атоме и может принимать целочисленные значения n = 1, 2, 3… .
2)
– орбитальное квантовое число, которое
при заданном n
принимает значения
и определяет момент импульса электрона
в атоме
.
При этом ясно, что момент импульса
(механический орбитальный момент)
принимает дискретные значения.
3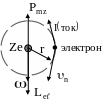
)
m
– магнитное квантовое число, которое
при заданном
может принимать значения
,
т. е. всего 2
+1
значений и определяет проекцию момента
импульса электрона на заданное направление
.
Механический
момент
,
где I – момент инерции.
- магнитный момент.
Отношение
называется орбитальным гиромагнитным
соотношением.
Тогда
.
Величина
- магнетрон Бора, равная
и являющаяся единицей измерения
.
Это говорит о квантуемости магнитного
момента.
Тогда магнитный
момент
- это говорит о квантуемости магнитного
момента.
Таким образом,
квантовые числа и их значения являются
следствием решений уравнения Шредингера
и условий однозначности, непрерывности
и конечности, налагаемых на волновую
функцию
.
3. Опыт Штерна и Герлаха. Спиновое квантовое число. Спин электрона
О. Штерном и В. Герлахом были поставлены опыты (1921г), целью которых являлось измерение магнитных моментов. Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле
,
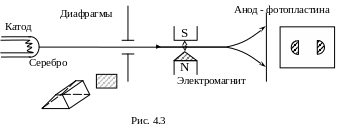
где B – индукция магнитного поля (направленного вдоль оси z) неоднородного только вдоль этой оси.
В трубку, где был создан вакуум, помещался источник пучка атомов, нагреваемый до высокой температуры серебряный шарик катод. Атомы серебра вылетали с его поверхности и через щелевые диафрагмы проходили через сильное неоднородное магнитное поле, направленное перпендикулярно пучку. Необходимая неоднородность была создана за счёт сильного электромагнита SN с полосными наконечниками специальной формы. Если бы момент импульса Le атома (и его магнитный момент Pm) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластину с большей плотностью паданий в середину и с меньшей по краям. Опыты, проведённые с серебром и атомами других элементов периодической системы привели к совершенно другому результату. На фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным ориентациям магнитного момента во внешнем поле.
Для объяснения
этого результата можно предположить,
что у электрона, помимо орбитального
момента импульса Le
и соответствующего ему магнитного
момента Рm,
имеется собственный механический момент
импульса LS,
который называется спином электрона и
который обладает соответствующим ему
собственным магнитным моментом
.
Из общих выводов квантовой механики
следует, что спин должен быть квантовым
по закону.
,
где S
– квантовое число, называемое спиновым
квантовым числом
.
.
Таким образом, проекция спинового механического момента импульса на направление поля может принимать два значения:
.
Проекция собственного магнитного момента электрона равна магнетону Бора:
.
Отношение
- спиновое гиромагнитное отношение, оно
в двое превышает орбитальное гиромагнитное
отношение.
Литература
1, глава III, § 14 17;