6. Корпускулярно-волновой дуализм

Вышеперечисленные и многие другие опыты показывают, что наряду с волновыми свойствами (проявления: дифракция, интерференция, дисперсия) электромагнитные волны проявляют и свойства корпускул – частиц. Таким образом, электромагнитное излучение как бы двуедино – проявляет и свойства частицы и свойства волны. Эта особенность получила название корпускулярно-волновой дуализм.

Литература

1, глава II, § 9  11.

2, глава 26, § 202  207.

3, глава 32.

Лекция № 3 Элементы квантовой механики

1. Корпускулярно – волновой дуализм свойств вещества. Гипотеза де Бройля. Дифракция электронов.

2. Границы изменения классической механики; соотношение неопределённостей Гейзенберга.

3. Уравнение Шредингера для стационарного состояния; волновая функция и её статистический смысл.

1. Корпускулярно – волновой дуализм свойств вещества. Гипотеза де Бройля. Дифракция электронов

Французский ученый Луи де Бройль, развивая представление о двойственной корпускулярно-волновой природе света, выдвинул в 1923 году гипотезу об “универсальности корпускулярно–волнового дуализма”. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи, наряду с корпускулярными обладают также волновыми свойствами.

Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс Р, а с другой – волновые характеристики – частота и длина волны . Количественные соотношения, связывающие корпускулярные и волновые свойства, такие же как и для фотонов

Е=h , P= .

Таким образом, любой частице, обладающей импульсом, сопоставляется волновой процесс с длиной волны, определяемой по формуле де Бройля:

.

С работ Луи де Бройля берет свое начало квантовая механика – раздел физики, который рассматривает поведение микрочастиц в тех случаях, когда ни корпускулярный, ни волновой процессы недостаточны для трактовки событий.

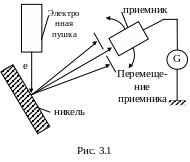
Гипотеза де Бройля вскоре была подтверждена экспериментально: американские физики Девиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки – кристалла никеля, – дает отчетливую дифракционную картину. Установка для дифракции электронов имеет вид, показанный на рисунке 3.1.

В последствии дифракционные явления обнаружили для нейтронов, протонов, атомных и молекулярных пучков.

Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и к макроскопическим телам. Почему же они не обнаружены экспериментально?

Например: частица массой m = 1 г, движущейся со скоростью  = 1м/с, соответствует волне де Бройля м. Такая длина волны лежит за пределами доступной наблюдению области. Поэтому считается, что макроскопические тела проявляют только корпускулярные свойства.

2. Границы изменения классической механики; соотношение неопределённостей Гейзенберга

Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства только частиц или все свойства только волн нельзя.

Необходимо внести некоторые ограничения в применении классической механики к объектам микромира.

В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы из-за наличия волновых свойств существенно отличаются от классических частиц. Основным различием является то, что нельзя говорить о движении микрочастиц по определенной траектории и не правомерно говорить об одновременных точных значениях ее координаты и импульса.

Гейзенберг пришел к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом.

Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определенную координату (x, y, z) и определенную соответствующую проекцию импульса (p_x; p_y; p_z ), причем неопределенности этих величин удовлетворяют условиям:

,

то есть произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

- точность определения положения координат.

Соотношение неопределенности является квантовым ограничением применимости классической механики микрообъекта.