Лекция № 12 Применение квантовой механики

1. Уравнение Шредингера для свободной частицы, находящейся в одномерной прямоугольной “потенциальной яме”. Квантование энергии.

2. Прохождение частиц сквозь потенциальный барьер. Туннельный эффект.

3. Линейный, гармонический осциллятор.

1. Уравнение Шредингера для свободной частицы, находящейся в одномерной прямоугольной “потенциальной яме”. Квантование энергии

Рассмотрим, как ведёт себя микрочастица в потенциальной яме. Для анализа движения ее необходимо использовать квантовую механику.

П усть электрон движется в бесконечно глубокой потенциальной яме с вертикальными стенками в направлении оси X от O до A, толщина стенок равна бесконечности (рис. 12.1).

Пусть потенциальная энергия электрона т. е. . Чтобы описать движение электрона в этой квантовой системе, используем уравнение Шредингера для одномерного пространства, в котором потенциальная энергия равна 0.

,

где .

Решением является функция , где A – амплитуда, – частота, – начальная фаза.

1. Определим, чему равна начальная фаза .

Из условия непрерывности функции и из условия того, что вероятность пребывания электрона за стенками потенциальной ямы равна 0, следует, что значения функции на краях ямы равны:

, тогда

, тогда .

2. Определим -частоту. Для её определения используем 2^e граничное условие: .

; где n=1,2,3…; .

Тогда, зная частоту, определим энергию электрона:

,

где n=1, 2, 3,…n – целое число.

Число n принимает дискретный ряд чисел (1,2,3…) при n=1 .

Из уравнения (1) следует, что энергия электрона принимает дискретный ряд значений. Значит, микрочастица в потенциальной яме может иметь только дискретный ряд значений энергии или величина энергии электрона квантована, n – главное квантовое число.

3. Определить значение А – амплитуды. Для этого используем условие нормировки функции.

;

; ;

.

Представим графически энергетические уровни электрона, волновую функцию , описывающую движение электрона в “потенциальном” ящике при условии, что u=0, соответствующую этим энергетическим уровням и плотность вероятности обнаружения частицы при различных расстояниях потенциальной ямы (рис. 12.2).

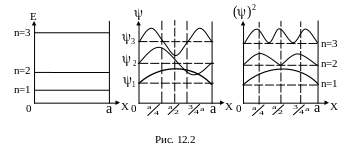
Если , то , , тогда .

При n=1 с наибольшей вероятностью электрон можно найти около середины ящика max; по краям вероятность равна 0.

При n=2 электрон не может быть обнаружен в середине и по краям ямы; вместе с тем одинаково часто бывает как в левой половине, так и в правой.

Отсюда видно, что такое движение электрона по оси X не совместимо с понятием механической траектории (рис. 12.2).

2. Прохождение частиц сквозь потенциальный барьер. Туннельный эффект

Движение электрона в “потенциальной” яме описывается волной де-Бройля, а на границе волна частично отражается и частично проходит (преломляется); значит, есть вероятность обнаружения электрона за пределами потенциальной ямы (рис.12.3).

Явление проникновения квантовой частицы (здесь электрона) за пределы потенциального барьера называется туннельным эффектом (12.4).

П

u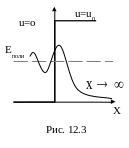

ри  .

При  .

Решением этого уравнения является функция вида: ,

.

М икрочастица, обладая волновыми свойствами, туннелирует через потенциальный барьер конечной длины, уменьшая интенсивность волны Де-Бройля, т. к. из уравнения Шредингера вытекает, что exp в любой степени не равно 0. Поэтому вероятность её обнаружения в потенциальном барьере и за его пределами не равна 0, хотя и невелика.

В связи с этим вводится понятие “прозрачности” потенциального барьера, показывающего вероятность просачивания микрочастицы через потенциальный барьер.

Прозрачностью потенциального барьера называется отношение вероятности появления частицы за потенциальным барьером (область III) к вероятности нахождения до потенциального барьера (область I).

.

Д ля потенциального барьера произвольной формы (рис. 12.5):

.

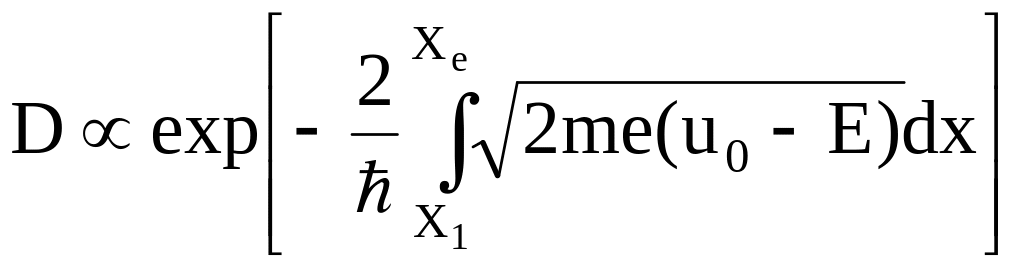С классической точки зрения прохождения частицы сквозь потенциальный барьер при невозможно, т. к. частица, находясь в области барьера, должна обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Таким образом, в квантовой механике деление на кинетическую и потенциальную энергии не имеет смысла из-за соотношения неопределённостей Гейзенберга.