3. Вырожденный электронный газ в металлах

Распределение электронов по различным квантовым состояниям подчиняются принципу Паули (не могут существовать в одной системе два электрона с одинаковым набором квантовых чисел). Следовательно, согласно квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Принцип Паули заставляет электроны взбираться вверх по “энергетической лестнице”.

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми-Дирака:

,

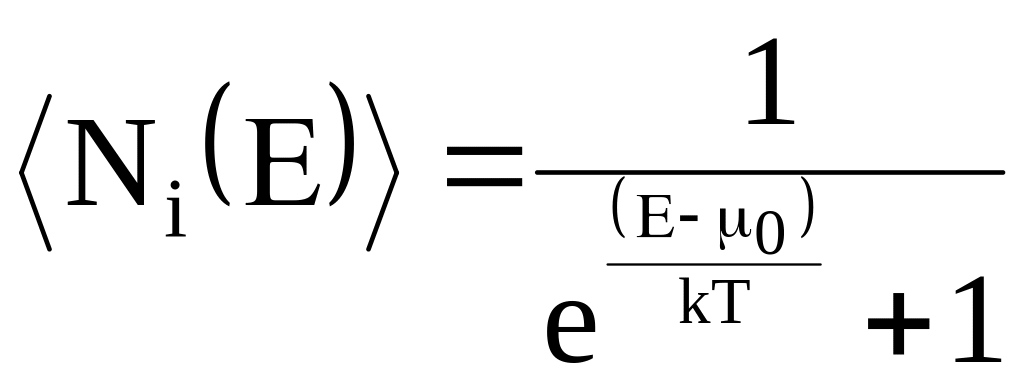где - химический потенциал электронного газа при Т= 0 К.

Для фермионов квантовое состояние может быть не заселено, либо в нем будет находиться одна частица. Это означает , где f(E) – функция распределения электронов по состояниям. При Т= 0 К функция распределения , если Е<₀; и при . График этой функции имеет вид (рис. 7.1).

В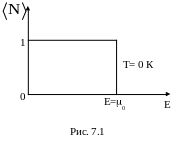 области энергий от 0 до ₀ функция равна 1 (рис. 7.1). При Е=₀ она скачкообразно меняется до 0. Это означает, что при Т= 0 К. Все нижние (с меньшей энергией) сквантовые состояния, вплоть до состояния , заполнены электронами, а все состояния с энергией большей ₀ свободны. Следовательно, ₀ есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная Е_кин называется энергией Ферми и обозначается . Поэтому распределение Ферми-Дирака обычно записывается:

.

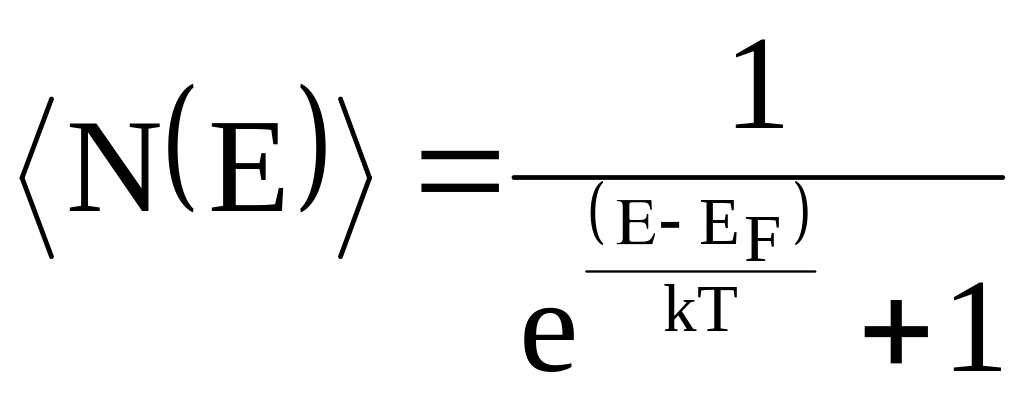Наивысший энергетический уровень, занятый электронами при 0 К, называется уровнем Ферми.

Уровню Ферми соответствует энергия Ферми Е_F, которую имеют электроны на этом уровне. Работу выхода электрона из металла нужно отсчитывать не от дна “потенциальной ямы”, как это делалось в классической теории, а от уровня Ферми, т.е. от верхнего из занятых электронами энергетических уровней.

Д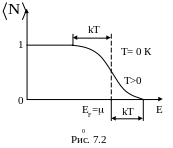 ля металлов при не слишком высоких температурах выполняется неравенство . Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т₀ вырождения находится из условия . При температурах, отличных 0 К, функция распределения Ферми-Дирака плавно изменяется от1 до 0 в узкой области порядка kT в окрестности E_F (рис. 7.2). Здесь же пунктиром показана функция при Т= 0 К.

При , т.е. при больших значениях энергий, к электронам в металле применима классическая статистика, в то же время, когда , к ним применима только квантовая статистика Ферми-Дирака.

4. Квантовая теория теплоемкости и электропроводности металлов

Квантовая статистика устранила трудность в объяснении зависимости теплоемкости газов от температуры.

Если энергия теплового движения значительно меньше разности энергий соседних уровней , то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному.

Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т.е. , то с ростом температуры возбуждаются вначале вращательные степени свободы, т.е. теплоемкость растет; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости.

Функция распределения Ферми-Дирака для Т = 0 и Т > 0 заметно различаются лишь в области энергий порядка kT. Следовательно, в процессе нагревания участвуют лишь незначительная часть электронов проводимости. Этим объясняется отсутствие заметной разности теплоемкостей металлов и диэлектриков.

Рассматривая непрерывный спектр частот осцилляторов (узлы кристаллической решетки), Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле.

Согласно принципу корпускулярно-волнового дуализма, упругим волнам в кристалле можно сопоставить некие частицы - фононы, обладающие энергией . Фонон – есть квант звуковой волны. Фононы являются квазичастицами – элементарными возбуждениями, ведущими себя подобно микрочастицам. Квазичастицы, в частности фононы сильно отличаются от обычных частиц (электронов, протонов, фотонов), т.к. они связаны с коллективным движением многих частиц системы. Импульс фонона обладает своеобразным свойством: при столкновении фонона в кристалле его импульс дискретными порциями передается кристаллической решетке, и импульс при этом не сохраняется. Поэтому говорят о квазиимпульсе.

Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняется статистике Бозе-Эйнштейна, т.к. фононы – это бозоны. Спин равен 0, для них . Исходя из этого, Дебай пришел к выводу, что при ; теплоемкость описывается по классической теории (закон Дюлонга и Пти), а при , , где - характеристическая температура Дебая, определяемая соотношением , где - предельная частота упругих колебаний кристаллической решетки.

Квантовая теория электропроводности металлов основана на квантовой механике и квантовой статистике Ферми-Дирака.

Выражение удельной электрической проводимости металлов

,

где n – концентрация электронов проводимости в металле; е – заряд электрона; - средняя длина пробега электрона, имеющего энергию Ферми; - средняя скорость теплового движения того же электрона.

В классической теории электропроводности Друде-Лоренца проводимость тоже обратно пропорциональна средней скорости теплового движения. Но , т.е. получается, что , что не подтверждается экспериментом. С квантовой же точки зрения - практически не зависит от температуры, а , т.е. или , что соответствует опытным данным.