Глава 43, § 433  434. Лекция № 7 Элементы квантовой статистики

1. Квантовая статистика. Фазовое пространство. Функция распределения.

2. Статистика Бозе-Эйнштейна и Ферми-Дирака.

3. Вырожденный электронный газ в металлах.

4. Квантовая теория теплоемкости и электропроводности металлов.

5. Сверхпроводимость. Эффект Джозефсона.

1. Квантовая статистика. Фазовое пространство. Функция распределения

Квантовая статистика – раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики. Она основывается на принципе неразличимости тождественных частиц.

Пусть система состоит из N частиц. Рассмотрим многомерное пространство, определяемое заданием 6N переменных, т.е. тройкой координат x, y, z и тройкой соответствующих проекций импульса . Это 6N – мерное пространство называется фазовым пространством.

Разобьем фазовое пространство на малые элементарные ячейки объемом

.

Такой объем элементарной ячейки называется фазовым объемом и не может быть меньше, чем (в соответствии с принципом неопределенности Гейзенберга), т.е.

.

Пусть есть вероятность данного состояния системы, определяемая функцией распределения .

Она показывает вероятность того, что точка фазового пространства попадет в элемент фазового объема dx, dp, расположенного вблизи точки x; p. Иными словами, dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале x, x+dx и p, p+dp функция распределения есть ничто иное, как плотность вероятности определенного состояния системы, поэтому она должна быть нормирована на единицу:

,

где интегрирование производится по всему фазовому пространству.

Зная функцию распределения , можно определить среднее значение величин (например, величина , характеризующая рассматриваемую систему:

.

Если иметь дело не с координатами x и импульсами p, а с энергией, которая квантуется, то состояние системы будет характеризоваться дискретной функцией распределения.

Явное выражение для функции распределения в общем виде получил Гиббс (это распределение называется каноническим распределением Гиббса).

,

где А – постоянная, определяется из условия нормировки; n – совокупность всех квантовых чисел; k – постоянная Больцмана; Т – температура термодинамическая.

2. Статистика Бозе -Эйнштейна и Ферми-Дирака

Одним из важнейших объектов изучения квантовой статистики является идеальный газ. Это связано с тем, что большинство квантовых систем можно в хорошем приближении считать идеальным газом.

Состояние системы невзаимодействующих частиц задается с помощью так называемых чисел заполнения - чисел, указывающих степень заполнения квантового состояния частицами системы, состоящих из многих тождественных частиц.

Для систем частиц, образованных бозонами – частиц с нулевым или целым спином, числа заполнения могут принимать любые целые значения 0, 1, 2,….

Для систем частиц, образованных фермионами – частицами с полуцелым спином, числа заполнения могут принимать значение: 0 – для свободных состояний и 1 – для занятых.

Сумма всех чисел заполнения должна быть равна числу частиц системы.

Квантовая статистика позволяет определить среднее значение чисел заполнения .

Идеальный газ из бозонов – бозе-газ – описывается квантовой статистикой Бозе-Эйнштейна. Распределение бозонов вытекает из распределния Гиббса и выражается:

- это распределение называется Бозе-Эйнштейна.

- среднее число бозонов в квантовом состоянии с энергией ;  - химический потенциал, не зависит от энергии, а определяется только Т и плотностью числа частиц. Определяет изменение внутренней энергии системы, при добавлении к ней одной частицы при условии, что энтропия, объем – фиксированы.

. При V = const, dS = const,

где Т – термодинамическая температура.

Идеальный газ из фермионов – ферми-газ описывается квантовой статистикой Ферми-Дирака.

Распределение фермионов по энергии имеет вид:

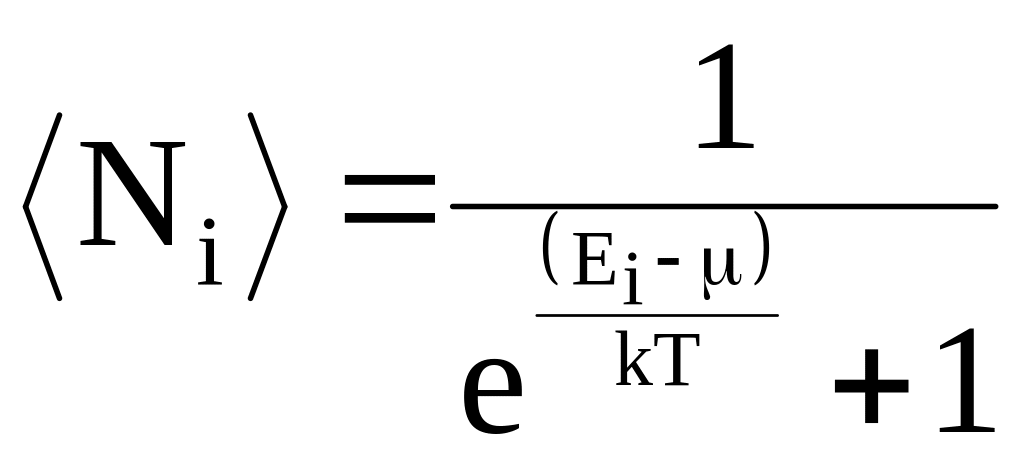- распределение Ферми-Дирака.

Если , то распределение Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана:

,

где .

Таким образом, оба газа при высоких температурах ведут себя подобно классическому газу.

Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств системы, подчиняющихся классической статистике.

Бозе-газ и ферми-газ являются вырожденными газами. Вырождение газов становится существенным при низких Т и больших плотностях. Параметром вырождения называется величина А. При A>>1 распределения Бозе-Эйнштейна и Ферми-Дирака переходят в распределение Максвелла-Больцмана.

Температурой вырождения Т₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа. Если Т>>Т₀, то поведение газа описывается классическими законами.