2. Распределение электронов в атоме по состояниям. Формула Бальмера

Состояние электрона в атоме однозначно определяется набором четных квантовых чисел:

Главного n (n=1, 2, 3, …);

Орбитального ;

Магнитного m_e (m_e= - …-1,0,+1,…,+ );

Магнитного спинового m_s=(m_s= + , - ).

Распределение электронов в атоме подчиняется принципу Паули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, , m_e и m_s, т.е.:

Z(n, L, m_e, m_s) = 0 или 1,

где Z(n, , m_e, m_s) - число электронов находится в квантовом состоянии.

Принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно формуле , данному n соответствует n² различных состояний, отличающихся значениями и m_e. Квантовое число принимает лишь два значения. Поэтому максимальное число электронов находится в состояниях, определяемых данным главным квантовым числом и равно:

.

Совокупность электронов, имеющих одно и то же главное квантовое число n, называется электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному . Поскольку , число подоболочек равно порядковому номеру n- оболочки.

Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовым числами: max число электронов в подоболочке с данным равно 2(2 +1).

Таблица обозначения оболочек и распределения электронов по оболочкам и подоболочкам

Главное квантовое число n	1	2		3			4				5
Символ оболочки	K	L		M			N				O
Max число электронов в оболочке	2	2n2 8		18			32				50
Орбитальное квантовое число	0	0	1	0	1	2	0	1	2	3	0	1	2	3	4
Символ подоболочки	1S	2S	2P	3S	3P	3d	4S	4P	4d	4f	5S	5P	5d	5f	5d
Max число электронов в подоболочке 2(2 +1)	2	2	6	2	6	10	2	6	10	14	2	6	10	14	18

Если известны 3 квантовых числа (n, , m_e) то .

Е сли известны 2 квантовых числа (n, ) то .

Если известно 1 квантовое число (n) то .

( - обозначение электрона; N- количество электронов)

¹¹Nа = 1S²2S²2P⁶3S¹ - пример электронной формулы.

Формула Бальмера.

Исследование спектров излучения разреженных газов (т.е. отдельных атомов) показали, что каждому газу присущ вполне определенный линейчатый спектр, состоящий из отдельных спектральных линий. Швейцарский ученый И. Бальмер подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:

,

где - постоянная Ридберга.

Так как , то:

, ,

где .

Ф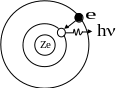 ормула Бальмера дает возможность рассчитать либо энергию фотона, либо частоту, при переходе электрона с одного энергетического уровня на другой. Она справедлива для водорода и водородоподобных атомов.

Из второго постулата Бора :

для Н .

- энергия фотона.

,

где K-слой, на который переходит электрон; L-слой, с которого переходит электрон.

- для водородоподобных атомов.

При переходе всех электронов с уровней на уровень n = 1 называется серией Лаймана.

При переходе с на уровень n = 2 называется серией Бальмера.

При на n = 3 - серия Пашена.

При на n = 4 - серия Бреккета.

При на n = 5 - серия Пфунда.