
- •Введение
- •I. Электрический заряд. Закон сохранения заряда. Закон кулона. Электрическое поле
- •1.1. Теоретические основы
- •1.2. Примеры решения заданий для выполнения расчётно-графических работ
- •Решение
- •1.3. Задания для расчетно-графических работ Расчётно-графическая работа 1
- •Расчётно-графическая работа 2
- •II. Электрический диполь. Дипольный момент системы электрических зарядов
- •2 .1. Теоретические основы
- •2.2. Примеры решения заданий для выполнения расчётно-графических работ
- •Решение
- •Решение
- •2.3. Заданиея для расчетно-графических работ Расчётно-графическая работа 3
- •III. Вычисление полей с помощью теоремы гаусса
- •3.1. Теоретические основы
- •3.2. Примеры решения заданий для выполнения расчётно-графических работ
- •Решение
- •Р ешение
- •3.3. Задания для расчетно-графических работ Расчётно-графическая работа 4
- •Расчётно-графическая работа 5
- •IV. Электроёмкость. Конденсаторы
- •4.1. Теоретические основы
- •4.3. Задание для расчетно-графических работ Расчётно-графическая работа 6
- •V. Требования к содержанию отчёта и решению задач расчётно-графической работы
- •VI. Рекомендации к защите отчета по ргр
- •VII. Справочные таблицы
- •Основные величины, их обозначение и единицы величин в си
- •Производные единицы си, имеющие наименование
- •Производные единицы физических величин
- •VIII. Рекомендуемая учебно-методическая литература
- •Содержание
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Национальный минерально-сырьевой университет ”Горный”
Кафедра Общей и технической физики
ЭЛЕКТРОСТАТИКА
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ЗАДАНИЯ
ДЛЯ РАСЧЁТНО-ГРАФИЧЕСКИХ РАБОТ
Учебное пособие
САНКТ-ПЕТЕРБУРГ
2012
УДК 530.10
ББК 22.33
Э455
Авторы: Н.Н. Смирнова, Н.С. Пщелко, В.И. Чернобай, В.В. Фицак
Изложены краткие теоретические основы электростатики, требования к содержанию расчетно-графических работ, рекомендации к подготовке и выполнению заданий. Приведены варианты индивидуальных заданий, справочные материалы, примеры решения и оформления заданий, помогающие при выполнении расчётно-графических работ
Учебное пособие подготовлено в соответствии с программой по дисциплине физика Государственного образовательного стандарта по направлению подготовки выпускников технических специальностей вузов и адресовано студентам всех форм обучения.
Научный редактор доц. Н.Н. Смирнова
Рецензенты:
Электростатика. Теоретические основы и задания для расчётно-графических работ: Учебное пособие/ Н.Н. Смирнова, Н.С. Пщелко, В.И. Чернобай, В.В. Фицак; Национальный минерально-сырьевой университет ”Горный”. СПб, 2012. 52 с.
ISBN
УДК 530.10
ББК 22.33
ISBN |
© Национальный минерально-сырьевой университет ”Горный”, 2012 г. |
Введение
В процессе изучения курса «Электродинамика», в соответствии с требованиями программы, студенты должны овладеть знаниями из его различных разделов, в том числе по «Электростатике», приобрести соответствующие компетенции и следующие навыки:
– проводить самостоятельный поиск необходимой информации с использованием различных источников (учебных, справочных и научно-популярных изданий, ресурсов интернета);
– применять математический аппарат для аналитического решения физических задач;
– анализировать, выполнять сравнительную оценку и делать выводы по результатам работы;
– использовать в решениях и представлении результатов (в виде рисунков, схем, таблиц и графиков) основные программные средства.
Лучшей оценкой степени освоения материала учебной программы является умение студента использовать приобретённые теоретические знания в решении конкретных задач. А уровень подготовки будущего специалиста зависит от способности студента выполнять самостоятельно задания различной степени сложности.
Одним из подходов к формированию необходимых для будущих выпускников компетенций у студентов, обучающихся по дисциплине «Физика» является использование традиционных фондов оценочных средств, к которым относятся расчётно-графические работы (РГР), разрабатываемые кафедрами по соответствующим дисциплинам.
Как оценочное средство расчётно-графическая работа позволяет преподавателю оценить знания, умения и уровень приобретенных студентами компетенций. Как обучающая технология она формирует у студентов умение определить, описать и объяснить физические понятия, явления, процессы и величины.
Выполнение студентами расчётно-графических работ способствует наиболее глубокому изучению теоретических основ соответствующего раздела курса физики.
При этом студенты получают знания по физике в процессе самостоятельной творческой работы, сочетая изучение физики с прикладными возможностями математики и информатики.
В пособии представлены задания по электростатике различной степени сложности.
I. Электрический заряд. Закон сохранения заряда. Закон кулона. Электрическое поле
1.1. Теоретические основы
В электростатике рассматриваются свойства и взаимодействия неподвижных в инерциальной системе отсчёта электрически заряженных тел или частиц, обладающих электрическим зарядом.
Электрический заряд это физическая величина, характеризующая свойство заряженных частиц или тел вступать в электромагнитные взаимодействия и определяющая величину сил и энергий при таких взаимодействиях.
Все
тела в природе способны электризоваться,
т.е. приобретать электрический заряд.
Наличие электрического заряда проявляется
в том, что заряженное тело взаимодействует
с другими заряженными телами. В природе
существуют два вида электрических
зарядов. Условно их называют положительными
и отрицательными. Заряды одного знака
отталкиваются, разных знаков –
притягиваются друг к другу. Самым
маленьким является заряд элементарных
частиц. Этот заряд называется элементарным.
Абсолютное значение элементарного
заряда
![]() Кл. Устойчивыми частицами, которые
входят в состав любого вещества, являются
электрон (элементарный заряд отрицательный)
и протон (элементарный заряд положительный).
Кл. Устойчивыми частицами, которые
входят в состав любого вещества, являются
электрон (элементарный заряд отрицательный)
и протон (элементарный заряд положительный).
Если
каким либо образом создать в теле избыток
частиц одного знака, то тело окажется
заряженным. Электрический заряд
квантуется. Заряженное тело имеет заряд
q,
который равен целому числу элементарных
зарядов, т.е.
![]() ,
где N
– число элементарных зарядов.
[N]=безразмерная
величина, [q]=
Кл, [e]= Кл.
,
где N
– число элементарных зарядов.
[N]=безразмерная
величина, [q]=
Кл, [e]= Кл.
Заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других тел, с которыми он взаимодействует, называется точечным зарядом.
Величина заряда, измеряемая в различных инерциальных системах отсчёта, оказывается одинаковой.
Система называется электрически изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы.
Закон сохранения электрического заряда.
В электрически изолированной системе взаимодействующих заряженных тел, алгебраическая сумма электрических зарядов остаётся постоянной.
![]() , (1.1)
, (1.1)
где:
qi
–
i-ый
заряд системы,
![]() Кл;
п - число
зарядов.
Кл;
п - число
зарядов.
Закон сохранения электрического заряда является фундаментальным и тесно связан с релятивистской инвариантностью заряда.
Закон Кулона
Закон Кулона справедлив для взаимодействия неподвижных точечных зарядов, а также заряженных тел шарообразной формы, если их заряды равномерно распределены по всему объёму или по всей поверхности этих тел.
Формулировка закона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними
![]() , (1.2)
, (1.2)
где
![]() – сила
взаимодействия зарядов q1
и q2;
r
расстояние между зарядами; εо
– электрическая постоянная, ε –
диэлектрическая проницаемость среды;
– сила
взаимодействия зарядов q1
и q2;
r
расстояние между зарядами; εо
– электрическая постоянная, ε –
диэлектрическая проницаемость среды;
![]() – орт-вектор
направления действия силы.
– орт-вектор
направления действия силы.
Линейная плотность заряда
![]() , (1.3)
, (1.3)
Поверхностная плотность заряда
![]() , (1.4)
, (1.4)
Объёмная плотность заряда
![]() , (1.5)
, (1.5)
где dq – элементарный заряд; d, dS, dV – элементы длины, площади и объема.
Электрическое поле.
Всякий электрический заряд или заряженное тело изменяет свойства окружающего его пространства, создавая в нём электрическое поле. Электрическое поле проявляет себя в действии силы на электрический заряд, помещённый в какую-либо точку этого поля.
Векторной силовой характеристикой электрического поля является напряжённость поля.
Напряженность электрического поля
![]() , (1.6)
, (1.6)
здесь q - заряд, помещенный в электрическом поле (пробный заряд).
Пробный заряд должен быть настолько мал, чтобы он не мог исказить исследуемое с его помощью поле.
Если
q
> 0, вектор
![]() направлен по
;
если q
< 0, векторы
и
имеют противоположные направления.
направлен по
;
если q
< 0, векторы
и
имеют противоположные направления.
Напряженность поля точечного заряда в вакууме
![]() , (1.7)
, (1.7)
где ![]() – радиус-вектор, соединяющий заряд q
с точкой, в которой вычисляется
напряженность поля; q
– точечный заряд, создающий поле;
– радиус-вектор, соединяющий заряд q
с точкой, в которой вычисляется
напряженность поля; q
– точечный заряд, создающий поле; ![]() – электрическая постоянная.
– электрическая постоянная.
Если q > 0, вектор направлен по радиус-вектору от заряда; если q < 0 – к заряду (см. рис.1).
Error: Reference source not found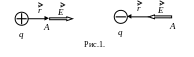
Однородное электрическое поле – поле, в каждой точке которого напряженность одинакова по величине и направлению.
Если не зависит от времени – однородное поле является стационарным (или постоянным).
Поле точечного заряда – неоднородное.
Принцип суперпозиции электрических полей: Напряженность электрического поля системы точечных зарядов в любой точке пространства равна геометрической сумме напряженностей полей каждого из этих зарядов в отдельности.
Заряды в пространстве распределяются либо дискретно, либо непрерывно.
В случае дискретного распределения электрических зарядов:
![]() , (1.8)
, (1.8)
г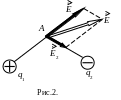 де
де
![]() – напряженность, создаваемая i-м
зарядом в рассматриваемой точке поля,
n
– число дискретных зарядов, входящих
в состав системы.
– напряженность, создаваемая i-м
зарядом в рассматриваемой точке поля,
n
– число дискретных зарядов, входящих
в состав системы.
Напряженность поля в точке А, создаваемая двумя точечными зарядами q1 и q2, (см. рис.2) равна
![]() . (1.9)
. (1.9)
где
![]() – напряженность, создаваемая зарядом
q1
в точке А.
– напряженность, создаваемая зарядом
q1
в точке А.
![]() – напряженность, создаваемая зарядом
q2
в точке А.
– напряженность, создаваемая зарядом
q2
в точке А.
Модуль напряженности в случае суперпозиции двух полей
![]() , (1.10)
, (1.10)
где α – угол между Е1 и Е2.
Напряженность электростатического поля, создаваемого системой неподвижных точечных зарядов q1, q2, …, qn:
![]() , (1.11)
, (1.11)
где
![]() – радиус-вектор, проведенный из точечного
заряда
– радиус-вектор, проведенный из точечного
заряда
![]() в рассматриваемую точку поля,
– электрическая постоянная.
в рассматриваемую точку поля,
– электрическая постоянная.
Энергетической характеристикой электрического поля является потенциал поля
![]() , (1.12)
, (1.12)
Потенциальная энергия поля точечного заряда
![]() . (1.13)
. (1.13)
Потенциал электрического поля точечного заряда q на расстоянии r от него
![]() . (1.14)
. (1.14)
Потенциал поля металлической сферы радиусом R, несущей заряд q на расстоянии r от центра
![]() ; (1.15)
; (1.15)
![]() . (1.16)
. (1.16)
Связь напряженности и потенциала электрического поля
![]() , (1.17)
, (1.17)
где gradφ – градиент потенциала.
Для сферической симметрии поля
![]() . (1.18)
. (1.18)
