
- •I курс, I семестр
- •Тема 1. Предел числовой последовательности.
- •Тема 2. Предел и непрерывность функции одной переменной.
- •Тема 3. Дифференцирование функции одной переменной.
- •Тема 4. Применение дифференциального исчисления к исследованию функций.
- •Тема 5. Неопределенный интеграл.
- •Вариант №1.
- •Вариант №2.
- •Вариант № 3.
- •Вариант № 4.
Тема 5. Неопределенный интеграл.
Семинар 15. Неопределенный интеграл. Непосредственное интегрирование.
№№ 1631, 1633, 1641, 1643, 1645, 1647, 1649, 1651, 1653.
Домашнее задание: 1632, 1634, 1642, 1644, 1646, 1650, 1652, 1662, 1664.
Семинар 16. Замена переменной в неопределенном интеграле.
№№ 1675, 1677, 1679, 1681, 1685, 1689, 1693, 1695, 1697, 1701.
Домашнее задание: 1674, 1676, 1679, 1678, 1686, 1690, 1698, 1704, 1708, 1710.
Семинар 17. Интегрирование по частям. Интегрирование рациональных функций.
№№ 17, 91, 1803, 1795, 1837, 1839.
Домашнее задание: 1792, 1802, 1798, 1838, 1840, 1866.
Семинар 18. Интегрирование тригонометрических и иррациональных функций.
№№ 1991, 2005, 2013, 2025, 1929, 1178, 1781, 1782.
Домашнее задание: 1995, 1997, 1998, 2004, 1926, 1780.
Список дополнительных задач. I семестр.
Вычислить пределы.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.
![]()
Вычислить пределы функций:
7.
![]() 8.
8.
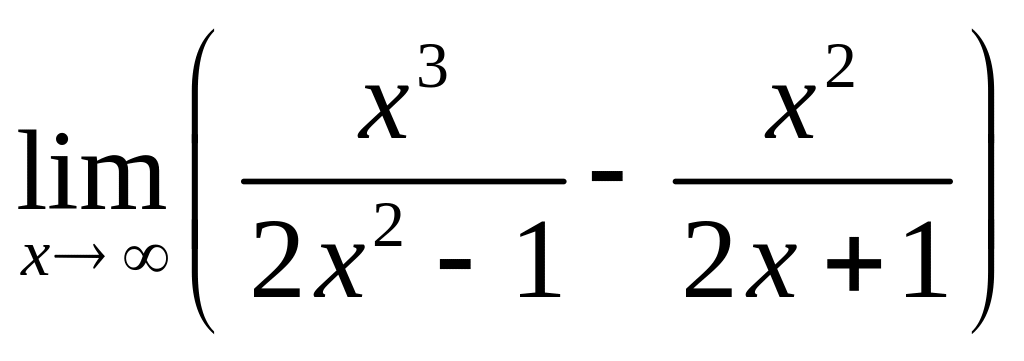 9.
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]() 13.
13.
![]() 14.
14.
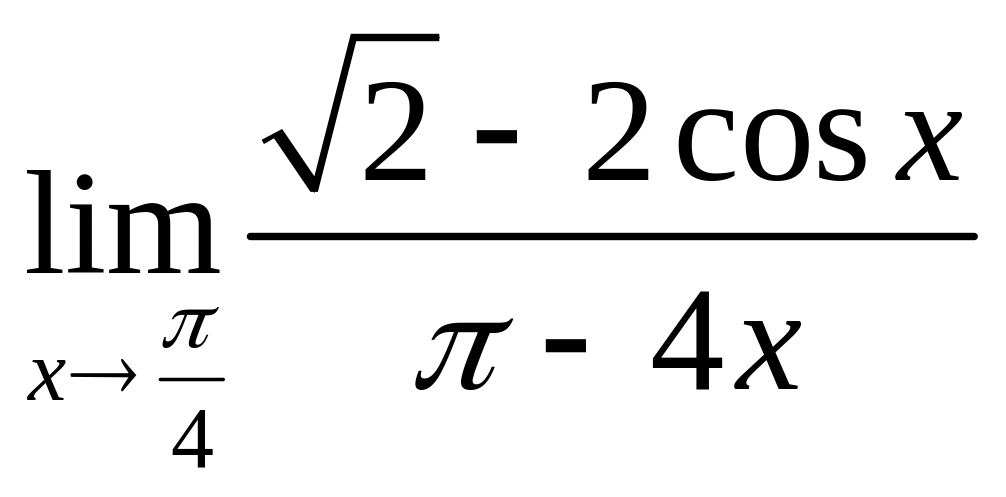
15.
![]() 16.
16.![]() 17.
17.
![]() 18.
18.
![]()
Исследовать функции на непрерывность:
19.
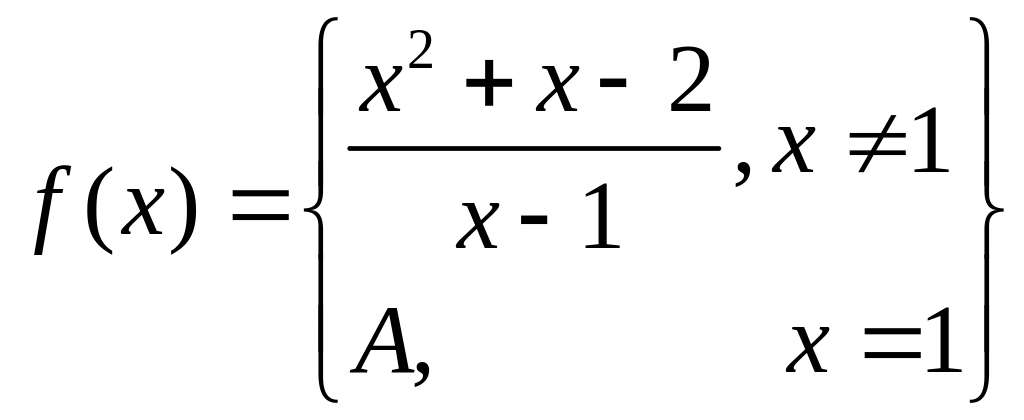 20.
20.
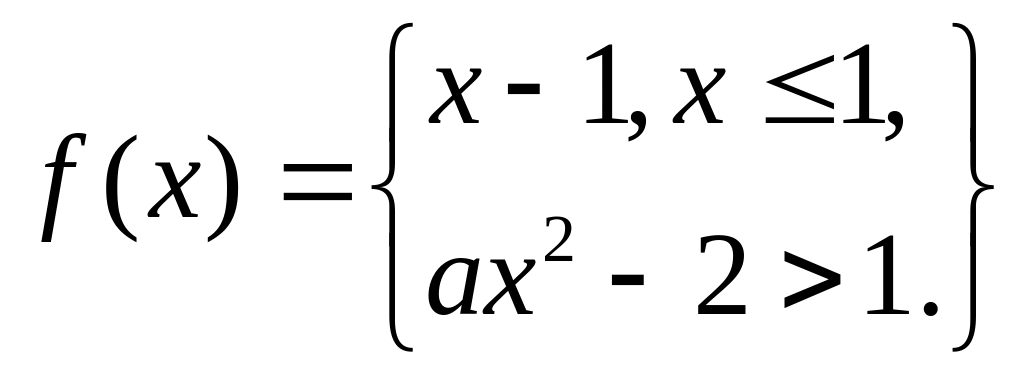
21.
![]() 22.
22.
![]()
![]()
23.
![]() 24.
24.
![]() .
.
Найти производные функций:
25.
![]() 26.
26.
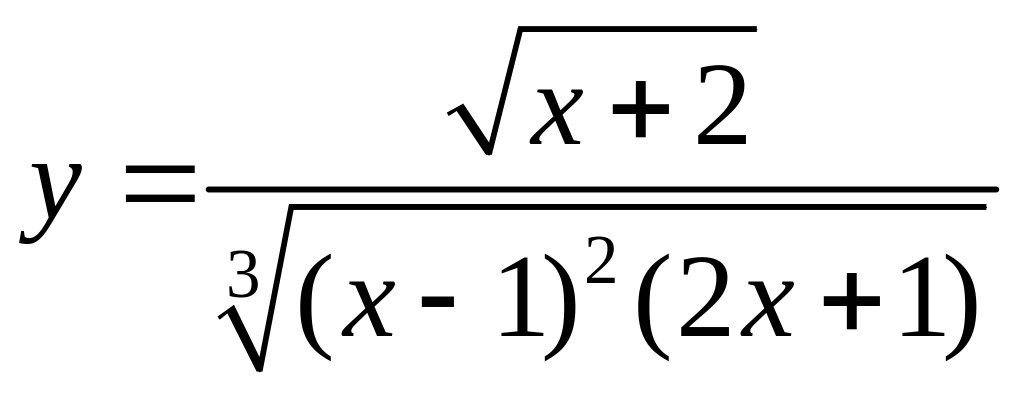 27.
27.
![]()
28.
![]() 29.
29.
![]() 30.
30.
![]()
Найти производные функций, заданных параметрически:
31.
![]() 32.
32.
![]()
![]()
Написать формулу Маклорена для следующих функций:
33.
![]() 34.
34.
![]() 35.
35.
![]()
36.
![]() 37.
37.
![]()
iV. Контрольная работа № 1
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
Вариант №1.
Вычислить пределы функций:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
Найти односторонние пределы функции:
1.
![]()
Найти точки разрыва функций и исследовать их характер:
1.
![]() 2.
2.
![]()
Вариант №2.
Вычислить пределы функций:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
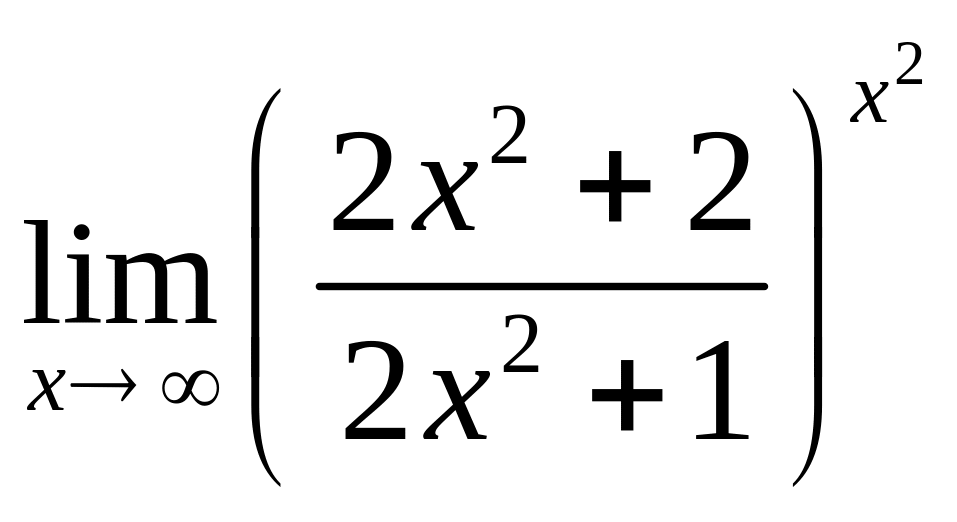
Найти односторонние пределы функции:
![]()
Найти точки разрыва функций и исследовать их характер:
1.
![]() 2.
2.
![]()
Вариант № 3
Вычислить пределы функций:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]() .
.
Найти односторонние пределы функции:
![]() .
.
Найти точки разрыва функций и исследовать их характер:
1.
![]() 2.
2.
![]() .
.
Вариант № 4
Вычислить пределы функций:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]() .
.
Найти односторонние пределы функции:
![]() .
.
Найти точки разрыва функций и исследовать их характер:
1.
![]() 2.
2.
![]() .
.
V. Контрольная работа № 2.
Дифференцирование функции одной переменной.
Формула Тейлора.
Вариант № 1.
Найти
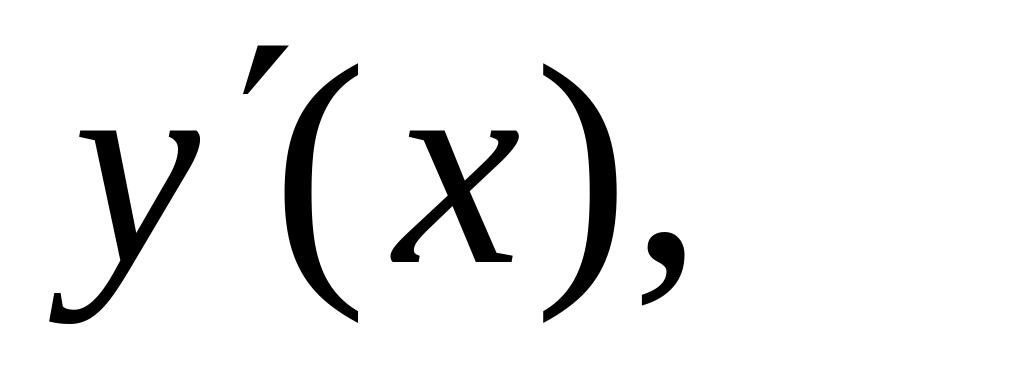 если
если
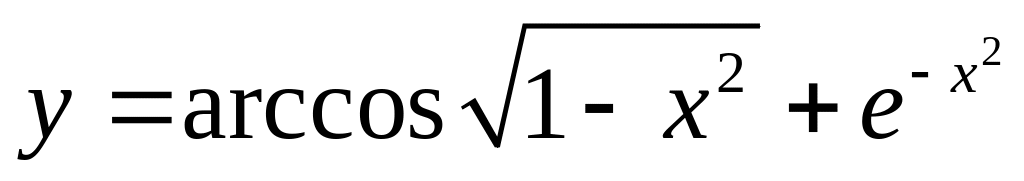
Найти
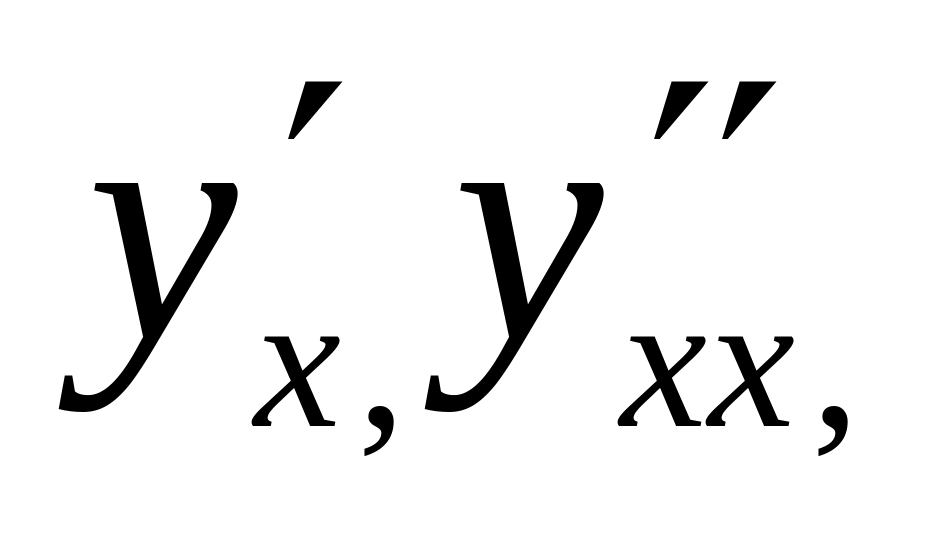 если
если

Найти
 если
если
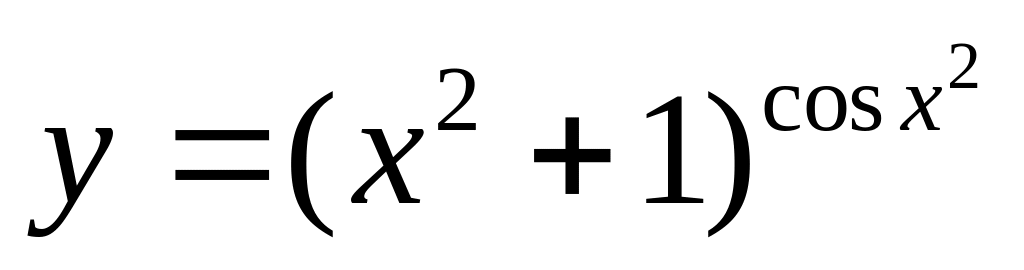 .
.
Найти
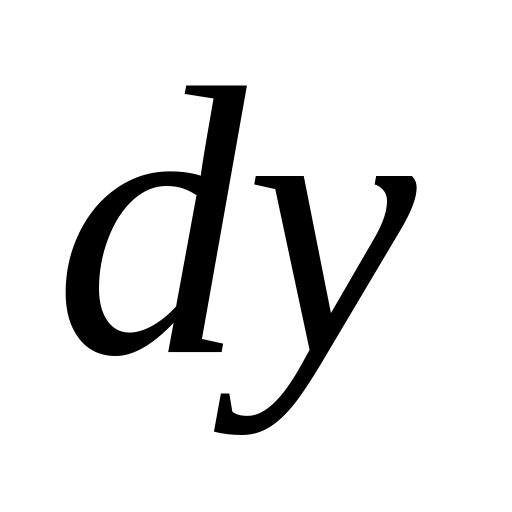 и
и
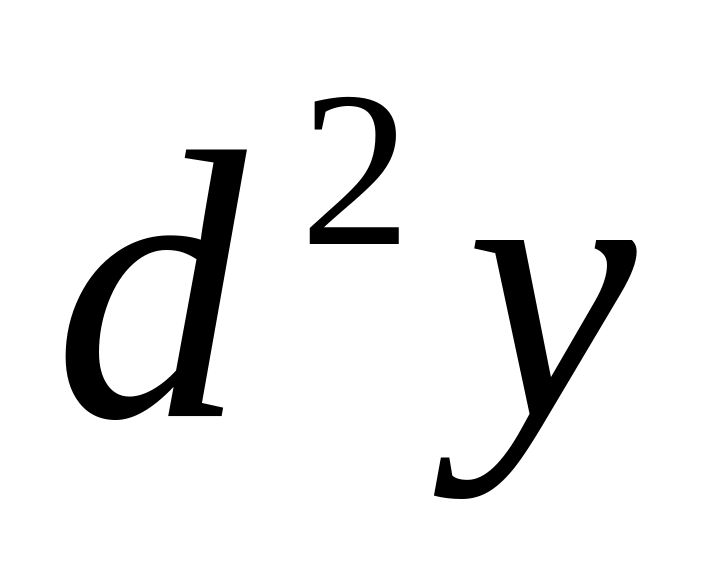 ,
если
,
если
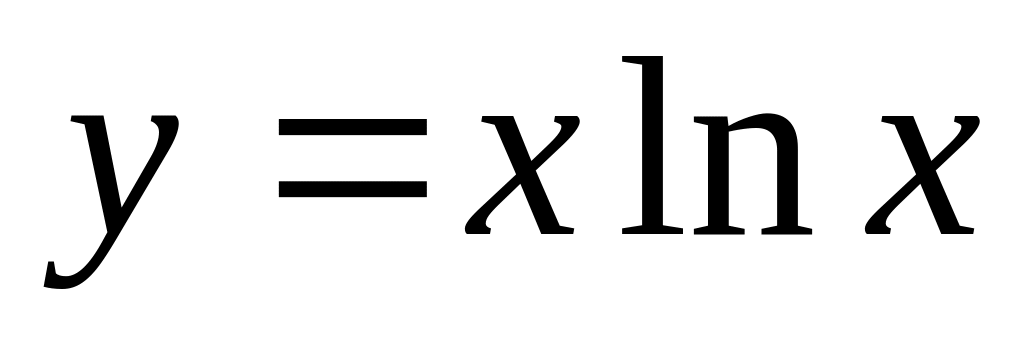 .
.
Используя разложения элементарных функций по формуле Маклорена, написать первые n членов формулы Маклорена (без остаточного члена) для функции
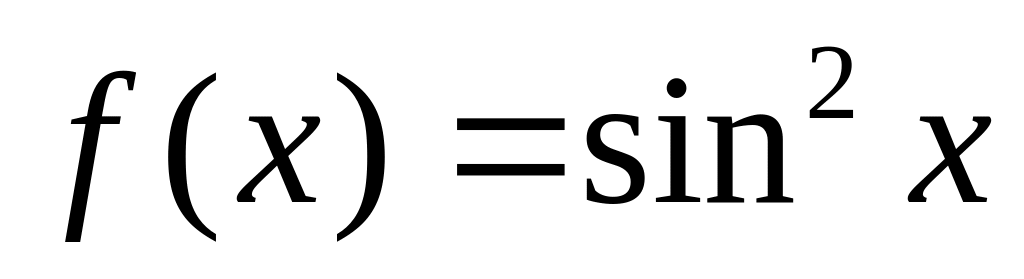 .
.
Пользуясь правилом Лопиталя, вычислить пределы:
6.
![]() 7.
7.
![]()
Вариант № 2.
Найти если
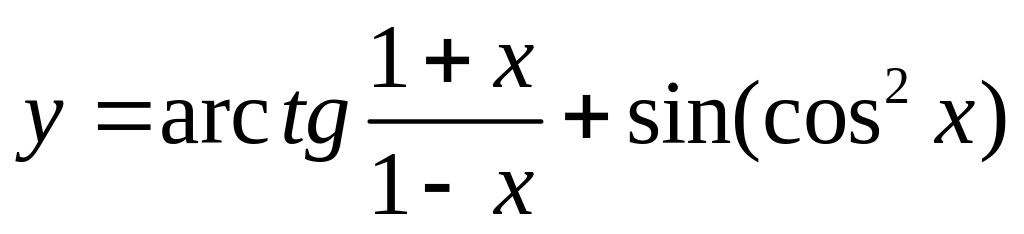
Найти если
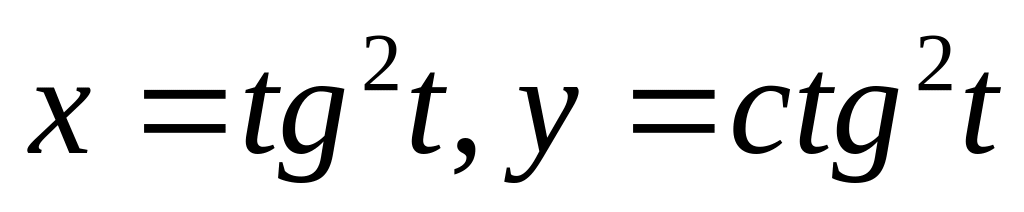
Найти если
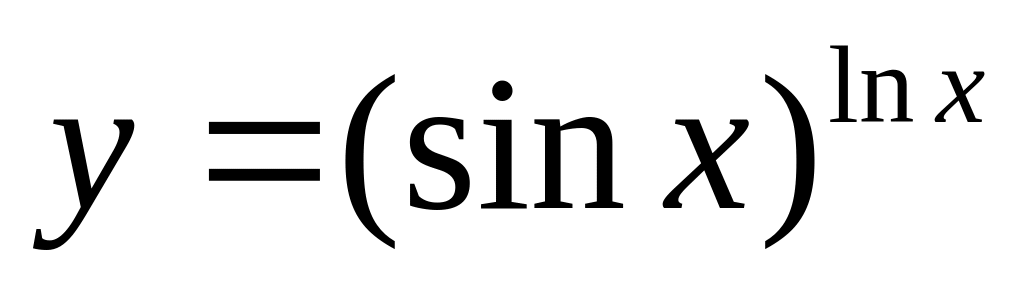 .
.
Найти и , если
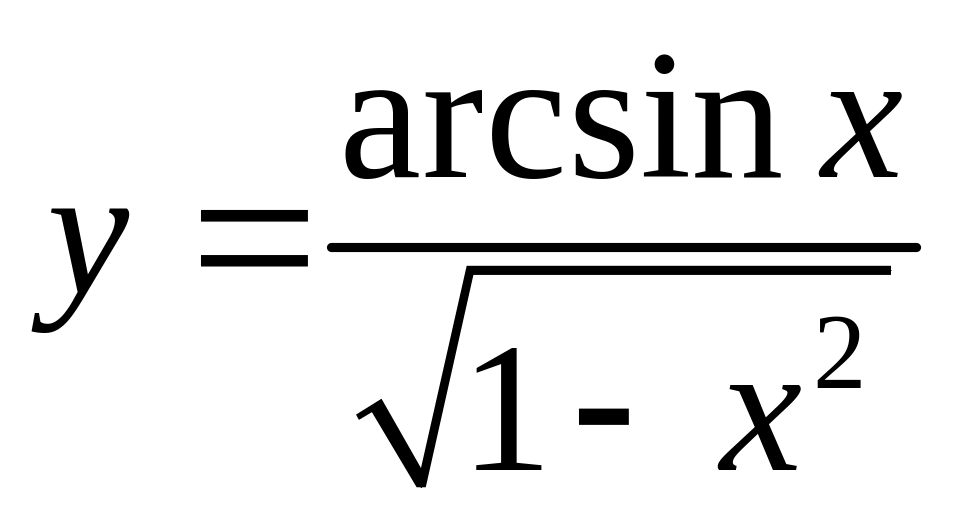 .
.
Используя разложение элементарных функций по формуле Маклорена, написать первые n членов формулы Маклорена (без остаточного члена) для функции
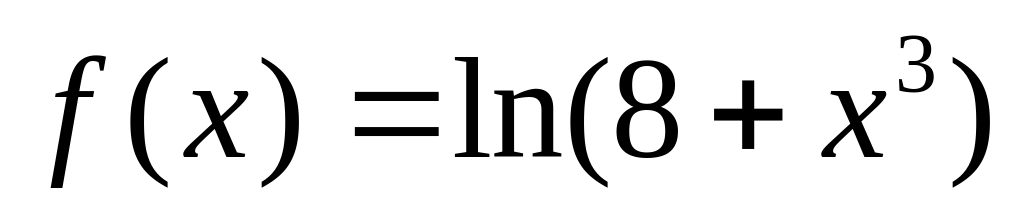 .
.
Пользуясь правилом Лопиталя, вычислить пределы:
6.
![]() 7.
7.
![]()
