
Контрольные вопросы
1. Что понимают под прямым кодом числа ?
2. Как образуется обратный код целого положительного числа?
3. Как образуется обратный код целого отрицательного числа ?
4. Каков алгоритм сложения чисел в прямом коде?
5. Каков алгоритм сложения чисел в обратном коде?
6. Чем характеризуется модифицированный обратный код?
1.2. Элементы алгебры логики
Лабораторная работа №1, Логические операции, равносильность формул.
Цель работы. Изучить логические операции и основные равносильности алгебры логики, научиться составлять таблицы истинности для формул алгебры логики и преобразовывать формулы, используя основные равносильности и правила поглощения.
Задание 1. Постройте таблицы истинности для высказываний
1) (X&Y)->X; 2) Xv(Y->X); 3) (X->Y)->X;
4) (X&Y)->(XvY); 5) (X <-> Y)-( Y); 6) (X&Y)<->X;
7) (X <-> Y)-> Y; 8) (XvY)<->(X->Y);
9) (X\/Y)->X&Y; 10) (X& Y) ->(X <-> Y).
Методические указания.
Пример.
Построить таблицу истинности для высказывания (XvY)->X.
X |
Y |
X\/Y |
X |
(XvY)->X |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Задание 2. Используя основные равносильности алгебры логики, докажите равносильность формул:
1) (X&Y)vX=X; 2) (X&Y)vX = X;
3) (X&Y)vX = X; 4) (X&Y)vX=XvY;
5) (X&Y) & (X&Y)= X,: 6) (XvY)&(YvZ)=(X&Z)vY.
Методические указания.
Основные равносильности алгебры логики:
1. А = А — закон двойного отрицания.
2. А &В = В & А — коммутативный закон для конъюнкции.
3. AvB = BvA — коммутативный закон для дизъюнкции.
4. (А & В) & С = А & (В & С) — ассоциативный закон для конъюнкции.
5. (A v В) v С = A v (В v С) — ассоциативный закон для дизъюнкции.
6. A & (B v С) = (A & B) v (А &С) — дистрибутивный закон.
7. A v (В & С) = (A v B) & (A v С) — дистрибутивный закон.
8. А & А =А — закон идемпотентности для конъюнкции.
9. A v A = А — закон идемпотентности для дизъюнкции.
10. (А & В) v А = А — закон поглощения.
11. (A v B) & А = А — закон поглощения.
12. A&B = AvB — закон де Моргана.
13. A v B = A&B — закон де Моргана.
14. А & 1 = А — закон единицы для конъюнкции,
15. А & 0 = 0 — закон нуля для конъюнкции.
16. A v 1 = 1 — закон единицы для дизъюнкции.
17. A v 0 = А — закон нуля для дизъюнкции.
Пример.
Доказать, что Xv(X&Y)=X.
Решение. Закон единицы для конъюнкции позволяет заменить X на X &1:
Xv(X&Y) = (X&l)v(X&Y).
Используя дистрибутивный закон, вынесем X за скобки:
Xv(X&Y) = (X&1)v(X&Y)=X&(1vY).
Закон единицы для дизъюнкции гласит 1vY = 1 , а закон единицы для дизъюнкции X&1 = X позволяет получить искомое выражение:
Xv(X&Y) = (X&1)v(X&Y) = X&(1vY) = X&1=X, что требовалось доказать.
Задание 3. Используя основные равносильности алгебры логики, а также равносильности, упростите формулы:
1) (Х-Х) -> Х; 2) (X->Y) -> Х;
3)(X<->Y)vX; 4)X&Y->X;
5) (X -> Y) -> (X -> Y);
6) (XvX)->( Y & Y);
7) (Х<-> Y)& (Y vX);
8) (X- >Y) &(Y->Z) -> (Z->X);
9) (X &Y)v(X&Y)v(Z&Y)v(X&Y&Z).
Методические указания.
Пример.
Используя основные равносильности алгебры логики, а также равносильности A->B=AvB и A<->B=(A->B)&(B->A)=(A&B)v (A&B), упростить формулу (X->Y) ->Y.
Решение.
(X->Y)->Y=(XvY)->Y =XvYvY=(X&Y)vY=(X&Y)vY = (XvY)&(YvY) =(XvY)&1 = XvY.
Ответ: (X-*Y)->Y=Xv Y.
Задание 4 (обобщающее).
Методические указания.
Логическую операцию «конъюнкция» в формулах алгебры логики можно опускать, т.е. выражение А&В можно записывать в виде АВ.
Пример.
Для заданного высказывания (X <-> Y) v (X -> YZ):
1) построить таблицу истинности;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
Решение.
Таблица истинности:
Пусть U = (X<->Y)v(X->YZ)
X |
Y |
Z |
X |
YZ |
X->YZ |
X<->Y |
U |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
l |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
l |
0 |
0 |
1 |
0 |
] |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2) Выполнить равносильные преобразования, используя X <-> Y = XYvXY и A->B = AvB, имеем:
(X <-> Y) v (X -> YZ) = (XY v ~Х Y) v (X v YZ) = XYvXYvXvYZ = XYvXvYZ =
(в последнем преобразовании для первого и третьего слагаемых использовали правило поглощения АВ v А =.А (I), далее использовать другое правило поглощения Av AB = Av В (2), получили)
= YvXvYZ = YvXvZ.
Еще раз использовали правило поглощения (2).
3) Для полученного выражения построить таблицу истинности:
X |
Y |
Z |
Y |
YvX |
Y v X v Z |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Результирующие (последние) столбцы в двух таблицах совпали, следовательно, выполненные преобразования верны.
Задания для самостоятельной работы
Для заданного логического выражения (высказывания):
1) построить таблицу истинности;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
Вариант |
|
Вариант |
|
1. |
(A<->B)vABvC |
2. |
(А->B)vACv ВС |
3. |
(AC->B)vAC |
4. |
ABv(A<->C)B |
5. |
(А -> В)(АС v ВС) |
6. |
(A~C)vABvAC |
7. |
(A->C)vABvBC |
8. |
(C-B)vACvBC |
9. |
(ВС ->A)vAC |
10. |
(AB ->C)vAC |
11. |
(А -> С)(ВС v АВ) |
12. |
(A <-> B)(A -> BC) |
13. |
(B->C)vABv АС |
14. |
(A -> BC) v ABvBC |
15. |
(AC ->B)vBC |
16. |
Bv(A<->CB)vAC |
17. |
(АС-> В) v ABC |
18. |
(A ~ C)(BC-> AB) |
19. |
(B->C)v(B->AC) |
20. |
(AB->C)vAv AC |
21. |
(A<->C)v(AB->C) |
22. |
(AB->C)vABC |
23. |
(AB ->C)vAC |
24. |
(A -> BС)(A - C) |
25. |
(А <->B)(A -> ВС) |
26. |
(A->B)(СA->В) |
Контрольные вопросы
/. Какие основные логические операции вам известны ?
2. Перечислите основные равносильности алгебры логики.
3. Постройте таблицы истинности для основных логических операций.
Лабораторная работа №2. Приложения алгебры логики
Цель работы. Изучить приложения алгебры логики к построению электронных схем и решению логических задач.
Логические элементы на комбинационных схемах имеют обозначения:
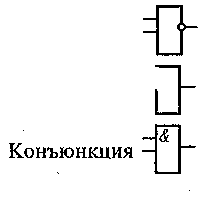
![]()
Отрицание
Дизъюнкция
Н![]() апример,
схеме -
соответствует формула а&Ь&с,
или
abc,
в
которой символ конъюнкции опущен. А
схема реализует формулу
avbvc.
апример,
схеме -
соответствует формула а&Ь&с,
или
abc,
в
которой символ конъюнкции опущен. А
схема реализует формулу
avbvc.
Пример 1.
Для заданной комбинационной схемы построить аналитическое выражение и, если возможно, равносильную ей упрощенную схему.
Здесь U = xl&x2, V=х3&х4,
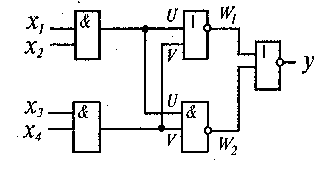
W1 = UvV = (xl&x2)v(x3&x4),
W2 = U & V = (xl & х2) & (хЗ & х4),
y = W1vW2= (xl & х2) v (х3 & х4) & (xl & х2) & (х3 & х4).
Преобразуем последнее выражение по закону де Моргана. Получаем у = ((xl & х2) v (хЗ & х4)) v (xl & х2) & (х3 & х4).
Используя законы ассоциативности и правила приоритета логических операций, получаем у = xlx2 v x3x4 v xlx2x3x4. Осталось воспользоваться правилом поглощения A v AB = А, в результате получим упрощенную формулу, равносильную данной у = xlx2vx3x4.
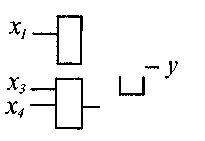
Ей соответствует упрощенная комбинационная схема
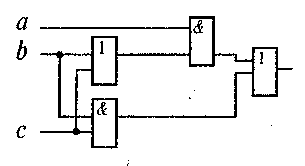
Пример 2.
Для заданной логической таблицы функции у(а,
а |
b |
с |
V |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Рассмотрим строки таблицы, в которых функция принимает значение 1. На базе этих строк построим элементарные конъюнкции по следующему правилу: единицу заменим именем аргумента, а нуль - именем аргумента с отрицанием. Полученные таким образом элементарные конъюнкции соединим знаками дизъюнкции. Для рассматриваемого примера имеем
(а & Ь & с) v (а & b & с) v (а & Ъ & с) v (а & b & с) = abc v abc v abc v abc. Объединим первое и четвертое слагаемые и вынесем за скобки bc, получаем bс{а v a) v abc vabc = bcvabcv abc. Объединим первое и второе слагаемые, вынесем за скобки с, а к выражению в скобках применим правило поглощения: Av АВ = Av В. Получаем
c(b v ab) v abc = c(b v a) v abc = bcv acv abc = be v a(c v be) =
= bcv a(cvb).
Найденному аналитическому выражению соответствует схема
Задания для самостоятельной работы
Задание 1. Для заданной комбинационной схемы постройте аналитическое выражение, упростите его с помощью равносильных преобразований и, если возможно, нарисуйте упрощенную схему.
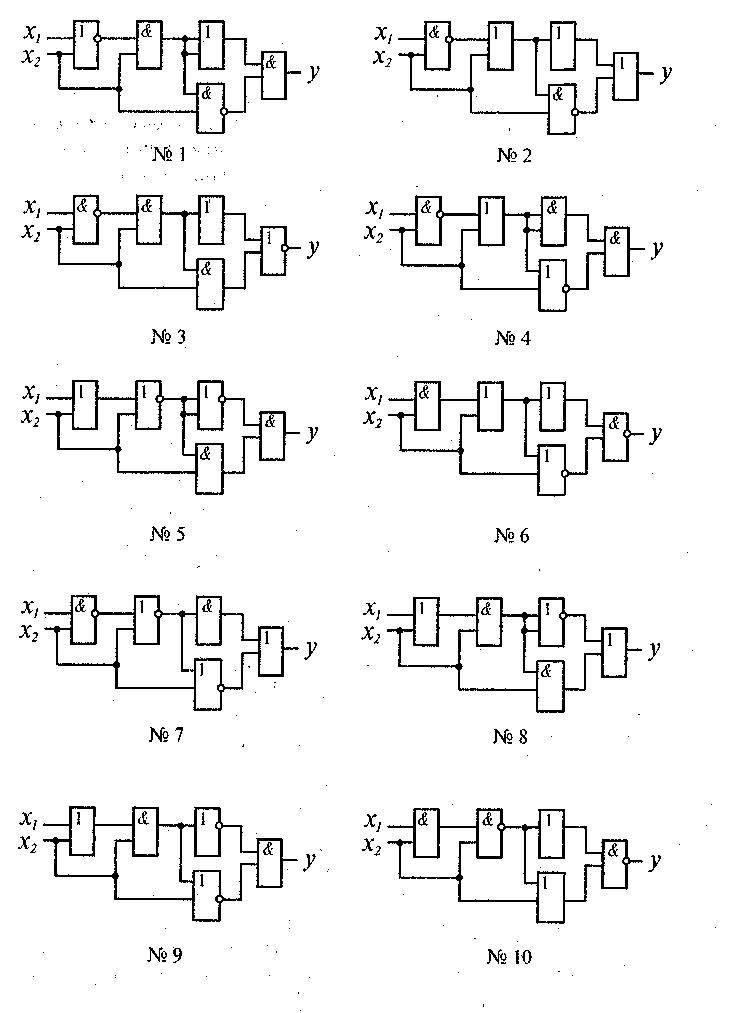


Задание 2.
Для заданной логической таблицы функции у(а, b,с) запишите аналитическое выражение и постройте комбинационную схему.

А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Вариант 14
Вариант 15
Вариант 11
Вариант 12
Вариант 13
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
А |
b |
c |
y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Решение логических задач средствами алгебры логики
Пример 3.
Рассмотрим задачу «Кто есть кто?», вошедшую в большинство учебников по математической логике.
По подозрению в совершенном преступлении задержаны Браун, Джон и Смит. Один из них — известный мошенник, другой — малоизвестный чиновник, третий — уважаемый старик. Известно, что старик всегда говорит правду, мошенник всегда лжет, а чиновник в одном случае лжет, в другом говорит правду. Их высказывания:
Браун: «Я совершил преступление, Джон невиновен».
Джон: «Преступник - Смит, Браун невиновен».
Смит: «Я невиновен, виновен Браун».
Определите имя старика, чиновника и мошенника и кто из них виновен в преступлении, если известно, что преступник только один.
Решение.
Обозначим буквами Б, Д, С соответственно высказывания: «виновен Браун», «виновен Джон», «виновен Смит». Тогда их утверждениям соответствуют формулы Б&Д, С&Б , С&Б . Запишем в виде таблицы смысловое значение этих формул.
Высказывания |
Виновен Браун |
Виновен Джон |
Виновен Смит |
Браун |
Да |
Нет |
|
Джон |
Нет |
|
Да |
Смит |
Да |
|
Нет |
По условию задачи один из них всегда лжет, т.е. одно из высказываний ложно. Так как кто-то всегда говорит правду, то одно из них истинно. Высказывание третьего также будет ложным как конъюнкция ложи и истины. Следовательно, из условия задачи вытекает, что только одно из этих высказываний может быть истинным. Получим истинную формулу:
и = (Б&Д)v/(С&Б)v(С&Б) = 1.
Составим для этой формулы таблицу истинности:
№п/п |
Б |
Д |
С |
Б |
Д |
С |
Б&Д |
С&Б |
С&Б |
U |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
3 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
5 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
6 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
7 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
8 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Из таблицы видно, что формула истинна только в пяти случаях, причем только в четырех из них истинна только одна конъюнкция, это строки с номерами 2, 4, 6, 7. Так как преступник только один, столбцы Б, Д, С должны содержать только одну единицу и Два нуля. В строках 4, 6, 7 оказывается по два истинных высказывания. Следовательно, остается только один случай, описанный строкой 2. Таким образом, определяем преступника — это Смит.
Так как преступник Смит, Джон говорил правду, а значит, старика зовут Джон. Оба высказывания Смита «Я не виновен» и «виновен Браун» ложны, так как мы уже знаем, что виновен он. Следовательно, Смит дважды лжет, и он — мошенник по условию задачи. Одно из высказываний Брауна: «Я совершил преступление» — ложно, а другое: «Джон невиновен» — истинно. Следовательно, Браун — чиновник.
Ответ: Джон — старик, Смит — мошенник (он же преступник), Браун — чиновник.
Пример 4.
Алекс, Боб, Джек и Сэм учатся в разных группах. Вот что они говорят:
Алекс: «Я студент 3-й группы, Сэм - 1-й». Боб: «Я студент 3-й группы, Алекс — 2-й». Сэм: «Я студент 2-й группы, Боб - 4-й».
Известно, чтобы запутать слушателей, каждый из них в одном высказывании говорит ложь, в другом правду. Определите, в какой из четырех групп учится каждый студент.
Решение.
Обозначим Ак, Бк, Дк, Ск высказывания «Алекс студент К-й группы», «Боб студент К-й группы», «Джек студент К-й группы», «Сэм студент К-й группы».
Рассмотрим высказывание Алекса, и предположим, что А3 = 1, тогда С, = 0. Тогда в высказывании Боба А^ = 0 (так как истина -«Алекс учится в 3-й группе») и Б3 = 1, а в высказывании Сэма Б4 = 0 (так как истина - «Боб учится в 3-й группе») иС,= 1.
Получили истинность высказываний: С2, А3, Б3. Этого не может быть, по условию задачи они студенты разных групп, а мы получили, что Алекс и Боб учатся в 3-й группе.
Пусть в высказывании Алекса А3 = 0, и С, = 1. Тогда в высказывании Сэма С2 = 0 и Б4 = 1, а в высказывании Боба А2 = 1, а Б3 = 0. В этом случае истинны высказывания: С,, А2, Б4.
Ответ: В 1-й группе учится Сэм, во 2-й — Алекс, в 3-й — Джек, в 4-й - Боб.
Задание 3 (для самостоятельной работы).
Кто из студентов А, В, С изучал информатику, если высказывание «Если изучал А, то и В изучал тоже» истинно, а «Если изучал С, то изучал и В» — ложно.
Определите, кто из трех студентов сдал экзамен, если известно:
«Если сдал первый, то и второй сдал».
«Если сдал второй, то и третий сдал».
«Если сдал третий, то второй сдал, а первый нет».
Указание. Решение постройте на основе таблицы истинности.
3) На экзамене пять студентов набрали 30, 35, 40, 45, 50 баллов. На вопрос: «Какой у вас балл?» они ответили следующее: Ален: «У меня — 30, у Джона — 40».
Боб: «У меня — 30, у Петра — 35». Петр: «У меня — 30, у Джона — 45». Джон: «У меня — 40, у Майкла — 50». Майкл: «У меня — 50, у Алена — 45».
Сколько баллов набрал каждый из них, если в их утверждениях одно ложное, а другое истинное?
4) Четырех друзей пригласили на праздник. Известно:
Если пригнел первый, то и второй тоже.
Если пришел второй, то не пришел первый или пришел третий.
Если пришел четвертый, то и первый тоже.
4. Если четвертый не пришел, то первый пришел, а третий - нет.
Определите, кто из них присутствовал на празднике.
Указание. Решение постройте на основе таблицы истинности.
5) После сдачи экзамена студенты придумали игру. Каждый из них информировал о результатах экзамена так, что одно из утверждений было ложно, а другое истинно.
«А набрал 90 баллов, а В — 60».
«А набрал 80 баллов, a F — 50».
«С набрал 80 баллов, a F — 70».
«С набрал 90 баллов, a D — 80».
«Е набрал 100 баллов, а В — 80».
Известно, что равное количество баллов не получил никто. Кто и какие баллы набрал в действительности?
