4.2 Виконати операцію віднімання чисел у двійковому коді:
(1ц3л)(1ц1л)(2ц1л)-(1ц8л)(2ц8л),
(1ц8л)(2ц8л)-(1ц3л)(1ц1л)(2ц1л).
Від'ємний результат подати у прямому коді. Після виконання вказаних операцій навести у шістнадцятковому коді значення операндів і результату. Синтезувати на базі повних однорозрядних суматорів функціональну схему багаторозрядного суматора, який виконує дані операції, і навести значення сигналів на входах схеми і на виходах кожного однорозрядного суматора. Синтезувати в базисі Буля функціональну схему повного однорозрядного суматора, навести його таблицю істинності і значення сигналів на входах суматора і на виходах кожного його елемента для кожного розряду згаданого вище багаторозрядного суматора.
(1ц3л)(1ц1л)(2ц1л) = 33516 = 0011 0011 01012
(1ц8л)(2ц8л) = 2816 = 0010 10002
Виконання операції +335 - 28
+335 + (-28);
0.0011 0011 0101 + 1.0000 0010 1000 - числа у прямому двійковому коді, крапка відділяє в даному випадку знак числа від значущих розрядів числа;
0.0011 0011 0101 + 1.1111 1101 1000 - числа у доповняльному двійковому коді;
0.0011 0011 0101
+
1.1111 1101 1000
0.0011 0000 1101 - результат додатній у двійковому коді.
0.30D - результат у прямому шістнадцятковому коді.
Відповідь: +30D.
335 - 28 = 30D
Виконання операції +28 - 335
+28 + (-335);
0.0000 0010 1000 + 1.0011 0011 0101 - числа у прямому двійковому коді, крапка відділяє в даному випадку знак числа від значущих розрядів числа;
0.0000 0010 1000 + 1.1100 1100 1011 - числа у доповняльному двійковому коді;
0.0000 0010 1000
+
1.1100 1100 1011
1.1100 1111 0011 - результат від'ємний у двійковому доповняльному коді.
5) 1.0011 0000 1101 - результат від'ємний у прямому двійковому коді.
1.30D - результат у прямому шістнадцятковому коді.
Відповідь: -30D.
28 - 335 = -30D
Таблиця істинності повного однорозрядного суматора:
Входи |
Виходи |
|||
A |
B |
Ci |
Co |
S |
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 0 0 1 0 1 1 1 |
0 1 1 0 1 0 0 1 |
З таблиці істинності видно, що
Co = /ABCi v A/BCi v AB/Ci v ABCi = BCi v ACi v AB;
S = /A/BCi v /AB/Ci v A/B/Ci v ABCi.
Функціональна схема повного однорозрядного сумматора:
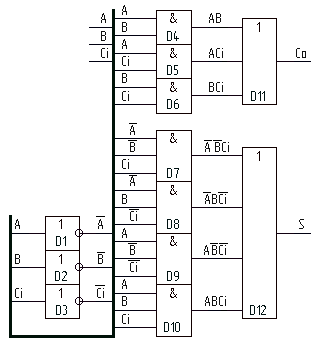
Операція « 335 - 28 » :
A |
B |
Ci |
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
D10 |
D11 |
D12 |
/A |
/B |
/Ci |
AB |
ACi |
BCi |
/A/BCi |
/AB/Ci |
A/B/Ci |
ABCi |
Co |
S |
|||
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
Операція « 28 - 335 » :
A |
B |
Ci |
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
D10 |
D11 |
D12 |
/A |
/B |
/Ci |
AB |
ACi |
BCi |
/A/BCi |
/AB/Ci |
A/B/Ci |
ABCi |
Co |
S |
|||
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |