Расчет переходных процессов по возмущающему воздействию

Переходная функция системы при единичном возмущающем воздействии, когда выходной величиной является выходная величина внешнего контура и на выходе системы имеется установившийся процесс с y₂=1.

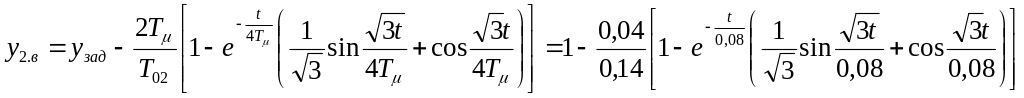
Для упрощенного случая

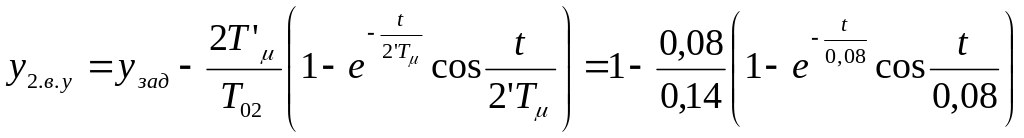
где .

Переходная функция системы при возмущающем воздействии, когда выходной величиной является выходная величина внутреннего контура, будет оптимальной

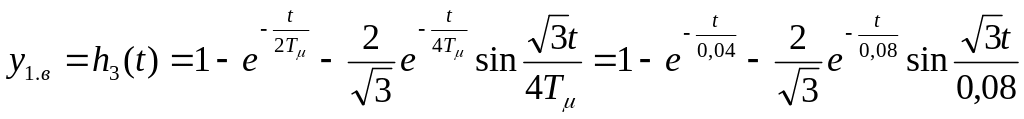
Для упрощенной САР

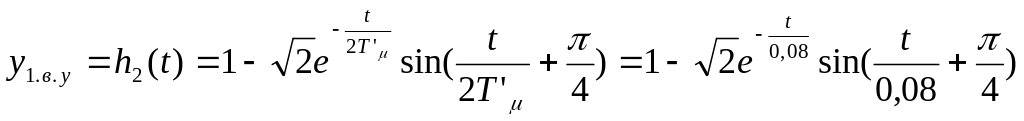
где .

Подставляя значения времени, строим кривые переходных процессов при возмущающем воздействии. Построение Расчет0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000кривых переходного процесса представим на рисунке 15. Построение начнем с момента времени До этого времени используем построение кривых при управляющем воздействии.

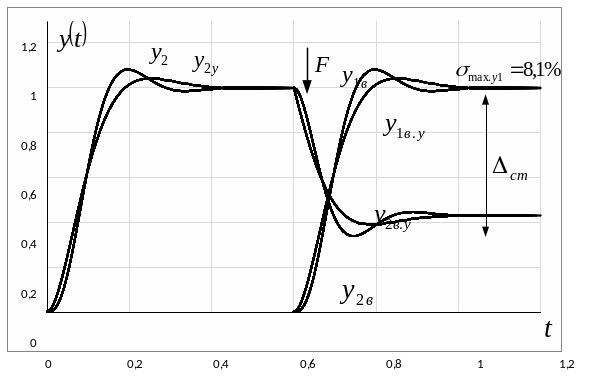
Рис. 15. Кривые переходного процесса при возмущающем воздействии

3.4. Расчеты построения переходных процессов статической сар по управляющему и возмущающему воздействию по методу структурного моделирования на цвм

С помощью программы MATLAB – Simulink проводится моделирование переходных процессов при управляющем воздействии

Рис. 16. Кривые переходных процессов САР по управляющему воздействию

Рис. 17. Кривые переходных процессов САР по возмущающему воздействию

3.5. Определение показателей качества статических сар

По полученным кривым переходных процессов могут быть получены основные статические и динамические показатели статических САР при управляющем и возмущающем воздействиях:

а) по управляющему воздействию

;

а) по возмущающему воздействию

;

Рассматриваемая система является статической по возмущению.

В установившемся режиме при выходной сигнал внутреннего контура и внешнего контура

4. Расчет исследования двухконтурной астатической сар с последовательной коррекцией

4.1. Структурная схема сар, настроенной по симметричному оптимуму. Расчет регулятора внешнего контура

Как показано ранее любой оптимизированный по “модульному” оптимуму контур регулирования может быть представлен колебательным звеном с передаточной функцией

.

где - наименьшая постоянная времени рассматриваемого контура с коэффициентом демпфирования .

В этом случае логарифмическая амплитудная частотная характеристика имеет вид кривой 1-1 на рис.18. Важнейшим достоинством таких систем является возможность получения оптимального переходного процесса с минимальными значениями перерегулирования и времени регулирования. Кроме того, такой метод оптимизации обеспечивает простоту построения и расчета таких оптимальных систем. Однако недостатком такого метода является то, что система регулирования в этом случае будет статической, поэтому в ряде случаев требования к точности регулирования не могут быть удовлетворены.

Из способа оптимизации по техническому оптимуму следует, что с целью придания оптимизированному контуру регулирования астатической характеристики в него вводится интегрирующее звено (если в объекте регулирования оно отсутствует). Обычно в рассматриваемых САР кроме управляющего воздействия имеется и возмущающее воздействие. В этом случае статическая ошибка регулирования при возмущающем воздействии может превысить допустимую величину. Для уменьшения, либо исключения ошибки в этом случае необходимо изменить настройку системы регулирования. Рассмотренная ранее система является астатической по управляющему воздействию и статической по возмущающему воздействию. Это значит, что при приложении возмещения возникает статическая ошибка, величина которой пропорциональна этому возмущению.

Для получения системы астатической и по возмущающему воздействию необходимо иметь два интегрирующих звена.

Но система, имеющая два интегрирующих звена, является структурно неустойчивой, т.к. её ЛАЧХ пересекает ось с наклоном . Для обеспечения устойчивости контура регулирования с двукратным интегрированием его ЛАЧХ (рис.18, кривая 2-2) должна повторять в зоне частоты среза наклон ЛАЧХ, равный .

Следовательно, ЛАЧХ двукратно интегрирующей системы в области частоты среза должна иметь наклон . А переход к двукратному интегрированию, т.е. переход в наклон , должен осуществляться левее частоты среза (на октаву), т.е. при , что симметрично по отношению к существующему перелому ЛАЧХ справа на одну октаву от частоты среза, т.е. . В связи с этим, такой способ оптимизации с двукратным интегрированием называется “симметричным оптимумом” по виду желаемой ЛАЧХ.

Передаточная функция разомкнутого контура регулирования, соответствующая ЛАЧХ, имеет вид

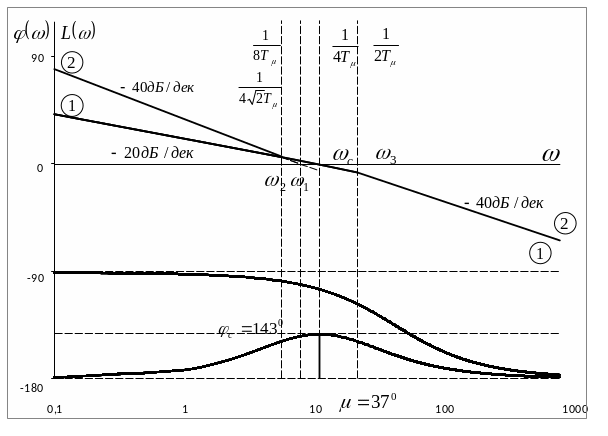
Рис. 18. ЛАЧХ и ЛФЧХ контура при настройке на симметричный оптимум

Увеличение наклона низкочастотной части ЛАЧХ до позволяет уменьшить динамические ошибки за счет увеличения коэффициента усиления в низкочастотной области ЛАЧХ. Логарифмическая фазовая частотная характеристика при этом также имеет симметричный характер относительно частоты среза . ЛФЧХ такой системы, рассчитанная по выражению , представлена на рис.18. Из этой характеристики видно, что максимум запаса по фазе будет иметь место примерно в середине среднечастотной амплитуды с наклоном .

Следовательно, система, настроенная по “симметричному оптимуму”, будет астатической с астатизмом второго порядка ( как по управляющему, так и по возмущающему воздействиям). Для ЛАЧХ такой системы имеем следующие пропорции частот:

; ;

; ; ;

Максимальный запас по фазе наблюдается при частоте среза рад/с.

Перерегулирование системы при частоте среза

При исследовании системы, оптимизированной по симметричному оптимуму, будем представлять внутренний контур как апериодическое звено первого порядка с постоянной регулирования с, т.е. по упрощенной схеме САР.

Чтобы получить систему с передаточной функцией , нужно чтобы передаточная функция второго регулятора представляла собой выражение

,

где - передаточная функция регулятора по техническому оптимуму.

Для уменьшения перерегулирования при управляющем воздействии в такой системе перед входом ставят фильтр с передаточной функцией

В соответствии с принципом оптимизации структурная схема САР, настроенной по симметричному оптимуму имеет вид.

Рис.19. Структурная схема САР, оптимизированная по симметричному оптимуму