2. Расчет и исследование внутреннего контура двухконтурных статических и астатических сар с последовательной коррекцией

2.1. Составление схемы оптимальной двухконтурной сар

Оптимальная схема САР составляется на основании принципа построения систем подчиненного регулирования. Согласно этому принципу число контуров регулирования, т.е. число регуляторов принимается равным числу больших постоянных времени. В нашем случае система должна содержать два контура регулирования с двумя регуляторами, один из которых компенсирует первую постоянную времени, а второй – вторую постоянную времени. Построение структурной схемы регулирования обычно начинают с внутреннего контура, в который входит звено с малой постоянной времени и одной большой постоянной времени. Перед объектом регулирования ставят регулятор W_р1(p) и охватывают единичной обратной связью. Затем строиться второй контур регулирования с второй большой постоянной времени. На вход ставят второй регулятор W_р2(p) (См. рис.2).

Рис.2. Структурная схема оптимальной двухконтурной САР

К САР приложены следующие воздействия:

- управляющее воздействие;

- внешнее возмущающее воздействие.

Регулируемыми выходными координатами являются:

- выходная регулируемая координата первого, внутреннего контура;

- выходная регулируемая координата второго, внешнего контура.

2.2. Структурная схема внутреннего контура регулирования сар. Определение передаточной функции регулятора внутреннего контура

Рис. 3. Структурная схема внутреннего контура регулирования двухконтурной статической САР

Передаточная функция регулятора внутреннего контура регулирования может быть найдена по обобщенной формуле

(1)

где – номер рассматриваемого контура;

– наименьшая некомпенсируемая постоянная времени;

- постоянная времени обратной связи регулятора;

- постоянная времени интегрирования регулятора;

– передаточная функция той части объекта регулирования, которая компенсируется регулятором первого контура;

– коэффициент обратной связи внутреннего контура регулирования ( ).

Таким образом, для регулятора имеем следующую передаточную функцию:

, (2)

т.е. регулятор имеет пропорционально-интегральную характеристику. Параметры регулятора могут быть найдены после подстановки в выражение (2) исходных данных объекта регулирования

(3)

2.3. Передаточные функции внутреннего оптимального разомкнутого и замкнутого контуров регулирования

Передаточная функция разомкнутого внутреннего контура

(4)

Следовательно, в разомкнутом внутреннем контуре имеется интегрирующее звено. Наличие такого звена в контуре регулирования приводит к тому, что в установившемся режиме (статике) отсутствует ошибка регулирования выходной величины y₁ в соответствии с заданным значением y₃₁ .

Передаточная функция замкнутого внутреннего контура

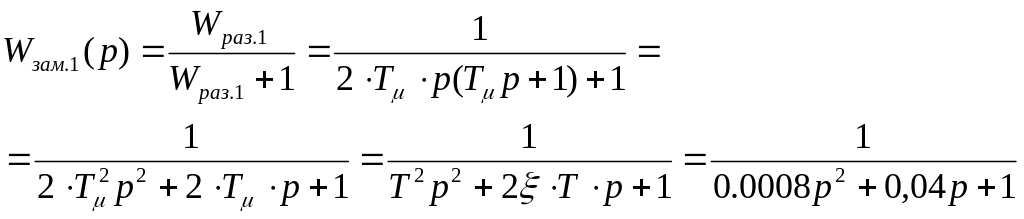(5)

где - эквивалентная постоянная времени внутреннего контура; - коэффициент демпфирования контура.

2.4. Аналитический расчет графиков переходных процессов оптимального внутреннего замкнутого контура сар

Применив обратное преобразование Лапласа, можно получить следующее выражение для переходной функции замкнутого контура.

(6)

Характеристическое уравнение для данного случая

Задаваясь временем t и пользуясь выражением (6) составляем таблицу 1 , а затем строим кривую переходного процесса (рис. 4).

Расчет данных для построения кривой переходного процесса

Таблица 1

t	0	0,02	0,04	0,06	0,08	0,1	0,12	0,14	0,16	0,18	0,2	0,24	0,3	0,4
h(t)	0	0,17	0,49	0,76	0,93	1,02	1,04	1,04	1,03	1,01	1	0,99	0,99	1

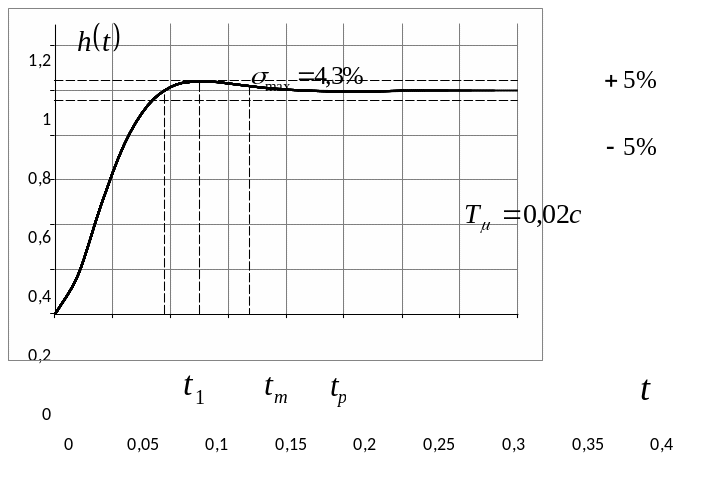
Рис. 4. Кривая переходного процесса h(t) внутреннего замкнутого контура САР

Переходная функция характеризуется следующими показателями:

- перерегулирование;

- время первого достижения установившегося значения;

- время достижения максимума;

- время переходного процесса (вхождение в 5% зону ошибки).