ВВЕДЕНИЕ

В настоящее время в подготовку специалистов технических вузов обязательно включается учебная дисциплина «Математика». В мае 2012 года в указах президент РФ В.В.Путин подчеркивал важность повышения качества обучения физике и математике.

Тема «Производная функции одной переменной», которая традиционно включается в раздел «Математический анализ» курса математики, стимулирует развитие у студентов аналитического мышления, умение сопоставлять известные формулы и результаты собственных исследований. Это способствует достижению основных целей образования: владеть методами количественного анализа и моделирования, теоретического и экспериментального исследования.

Основная часть представленных методических указаний содержит теоретические сведения о производной функции одной переменной, определения, таблицу производных элементарных функций, правила дифференцирования. Много места отведено решению практических задач. Здесь представлены типовые задания и тридцать. вариантов исходных данных к типовым заданиям для индивидуальной самостоятельной работы студентов двух уровней сложности.

Авторы выражают надежду, что представленная работа будет чрезвычайно полезна при организации самостоятельной работы студентов.

1. Задачи, приводящие к понятию производной

1. . Задача о вычислении скорости движущейся точки

Рассмотрим прямолинейное неравномерное движение некоторой материальной точки M. Расстояние S, на которое переместится точка M от начального положения за промежуток времени t, будет являться функцией времени Пусть в некоторый момент t точка M находилась на расстоянии S, а в некоторый следующий момент точка M находилась на расстоянии от начального положения . Таким образом, за величину времени величина S получила приращение Отношение дает среднюю скорость движения точки M за время Δt. Средняя скорость зависит от промежутка времени Δt и не может дать нам правильное представление об истинной скорости движения точки в момент t. Для более точного представления об истинной скорости движения в момент времени t необходимо взять как можно меньший промежуток времени Δt. Наиболее полно характеризует скорость движения точки в момент времени t тот предел, к которому стремится средняя скорость при Этот предел называют скоростью движения в данный момент:

(1)

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути ΔS к приращению времени Δt, когда приращение времени Δt стремится к нулю.

Учитывая, что равенство (1) запишем в виде:

(2)

Это и будет скорость неравномерного движения.

2. Задача о проведении касательной к кривой

Пусть дана кривая К и на ней точка М (рис. 1). Возьмем на кривой ещё какую-нибудь точку и проведем секущую Когда точка будет перемещаться вдоль кривой, эта секущая будет вращаться вокруг точки M.

О п р е д е л е н и е. Касательной к кривой К в точке М называется предельное положение МТ секущей , когда точка вдоль по кривой стремится к совпадению с M.

Д ля определения положения касательной к кривой в точке М достаточно знать угловой коэффициент касательной в точке M. Для любой кривой с уравнением угловой коэффициент устанавливается следующим образом. Приращению абсциссы Δx отвечает приращение Δy ординаты. Отношение выражает угловой коэффициент секущей tgφ. Угловой коэффициент k = tgα касательной в точке M получается путем перехода к пределу при Δx → 0:

(3)

Таким образом, угловой коэффициент касательной к кривой выражается как предел отношения приращения ординаты точки Δy к приращению абсциссы точки Δx, когда приращение абсциссы Δx стремится к нулю.

2. Определение производной, ее механический и геометрический смысл.

Сопоставляя операции, которые мы осуществляли при решении рассмотренных задач, легко усмотреть общие приемы. Обобщая их, придем к понятию производной.

Пусть функция определена на промежутке Х. При каждом значении аргумента из этого промежутка функция имеет некоторое значение.

Пусть аргумент получил приращение Δx произвольное по знаку. Тогда функция получит приращение Δy: Составим отношение приращения функции к приращению аргумента: Найдем предел этого отношения при Δx → 0:

Если этот предел существует, то его называют производной («произведенной») данной функции по независимой переменной x при данном её значении Обозначают производную одним из символов:

О п р е д е л е н и е. Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

(4)

Таким образом, если существует производная при данном значении то это определенное число. Если производная существует на всем промежутке, то она является функцией от x.

Пользуясь введенным понятием производной, можно указать несколько примеров выявляющих понятие производной:

1) Скорость v прямолинейного движения материальной точки в момент времени t есть производная от пройденного пути S по времени t, т. е. В этом заключается механический смысл производной.

2) Производная в точке x равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна x:

(5)

В этом заключается геометрический смысл производной.

3) Ускорение есть производная от скорости v по времени t, т. е.

4) Теплоемкость тела есть производная от количества тепла по температуре, т. е.

5) Сила тока есть производная от количества протекшего тока по времени, т. е.

Обобщая можно сказать, что если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса. В этом заключается физический смысл производной.

Операция нахождения производной называется дифференцированием.

По определению можно вычислить производную любой элементарной функции.

П р и м е р 1. Найти производные функций по определению:

а) y = x²; б) в) г)

Решение.

а) Придадим x приращение Δx. Тогда данная функция у получит приращение Составим отношение приращения функции к приращению аргумента Найдем предел этого отношения при Δx → 0 (по формуле 4), получим:

б) Придадим x приращение Δx, тогда данная функция у получит приращение (использовали формулу для разности синусов двух углов). Составим отношение приращения функции к приращению аргумента и найдем его предел при (формула 4): [учитывая, что при ]=

Следовательно,

в) Аналогично,

г)

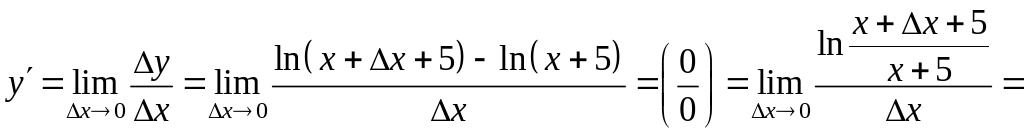
Проводя аналогичные рассуждения можно найти производные элементарных функций, которые приведены ниже.

3. Таблица основных формул дифференцирования

1	, где
2	в частности , ,
3		4
5		6
7		8
9		10
11		12

13		14
15		16
17		18