2. Регресійний аналіз впливу комфортабельності судна на рівень тарифів

2.1. Визначення характеру залежності між рівнем комфортабельності судна та рівнем тарифів

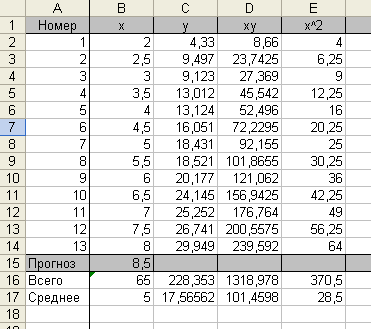
Для визначення характеру залежності між рівнем комфортабельності судна та рівнем тарифів необхідно на підставі статистичних даних(додаток А,Б)побудувати поля кореляції, на яких у відповідному масштабі по осі абсцис відбивається аргумент Х – відокремлено: коефіцієнт каютної комфортабельності, коефіцієнт загальної комфортабельності – по осі ординат визначається значення функції Y – рівня тарифної ставки.

Коефіцієнти розраховані по 32 суднам різних регіонів. Відповідно до регіону. обраному у п.1 вибираються 14 суден з тарифними ставками (додаток А) Завдання на вибірку 14 суден надаються викладачем індівідуально, залежно від регіону плавання (п.1) та його порядкового номеру:

Наприклад 1-й номер вибирає відповідно з 1-го. по 14судно та його тариф( додатокА):

,	Судно	Період круїзу	Тариф1
1	Сан Вайкинг	7
2	Сан Вайкинг	14	88,07
3	Нордик Принс	14	88,10
4	Сонг оф Норвей	7	90,57
5	Саугвард	7	89,32
6	Саугвард 2	3-4	87,42
7	Скайвард	7	81,30
8	Старвард	7	79,15
9	Норвей	7	94,33
10	Богема	7	79,74
11	Карнивэй	7	77,11
12	Марли Гра	7	76,50
13	Веендам	7	94,80
Продовження таблиці
14	Веендам	14	92,52
15	Волендам	7	99,13
16	Волендам	12	97, 55

Номер 2- слідуючі 14 суден.

Відповідно їм (додаток Б) надані розраховані коєфіціенти комфортабельності. Тарифи заносяться у стовбець B робочого листа MS EXEL,-це параметр(x) .У стовбець C парамерт (у) - коэфіціенти комфортабельності.

Ціль роботи виявити впливу коєфіціентів комфортабельності на рівень тарифної ставки

2.2. Визначення тісноти взаємозв’язку між рівнем коефіцієнта каютної та загальної комфортабельності судна та добовою тарифною ставкою

круїзу.

Блок вхідних даних формується в перших трьох стовпцях (А, В, С). За ним йде блок проміжних розрахунків (D, Е та ін.) Прогнозні дані обчислюються в рядку нижче вхідних даних. У cтовбец A- назва судна.

Таблиця 2.2

Вводиться гіпотеза, що між фактором х та показником y існує лінійна стохастична залежність .

Оцінки параметрів а і b парної регресії обчислюються за формулами:

Р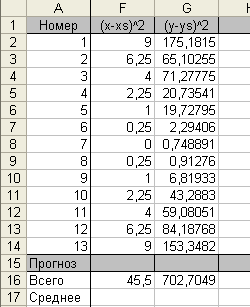 озрахуємо коефіцієнт кореляції :

, де =1,87, =7,35.(4)

Визначимо коефіцієнт детермінації:

.

Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використовуємо критерій Фішера. Перевіримо гіпотезу про статистичну незначність рівняння регресії .

4,84 (де , , ).

Для оцінки статистичної значності коефіцієнта кореляції використовується t- критерій Ст’юдента. Перевіряється гіпотеза про випадковий характер коефіцієнта.

.

24,64.

2,2 для , d.f.=11.

Для оцінки значності коефіцієнтів регресії знаходять надійні інтервали.

Випадкові помилки знаходять по формулам:

=0,16; =0,84; де =1.07.

Граничні помилки розраховуються по формулам:

=0,35; =1,86.

Надійні інтервали мають наступний вигляд: , .

,

Розрахуємо надійні зони базисних даних для кожного показника y:

• середня стандартна помилка ;

• гранична помилка ;

• надійний інтервал .

2,36 для ; d.f.=7.

Знайдемо прогноз показника та його надійні інтервали 31,2 для фактора .

Середня стандартна помилка = 1,23.

Гранична помилка =2,72.

Надійний інтервал .

Коефіцієнт еластичності для базисних даних та прогнозу обчислюється за формулою.

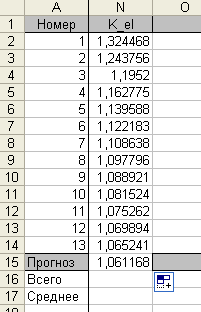
(5)

Вбудована статистична функція ЛИНЕЙН визначає коефіцієнти лінійної регресії y = ax + b.

• Треба виділити область пустих комірок 5х2 (5 строчок, 2 стовпця) для виводу результатів статистики регресії чи область 1х2 – для виводу тільки оцінок коефіцієнтів регресії.

• Далі активізуйте Майстер функцій і з розділу Статистичні треба вибрати ЛИНЕЙН.

• Далі треба заповнити діалогове вікно:

  • Відомі значення y – діапазон, в якому розташовані дані результативного признаку.

  • Відомі значення х – діапазон, в якому розташовані дані фактора незалежного признаку.

  • Константа – логічне значення, яке вказує наявність чи відсутність вільного члена в рівнянні. Якщо Константа = 1, то вільний член розраховується звичайним образом, якщо Константа = 0, то вільний член дорівнює 0.

  • Статистика – логічне значення, яке вказує чи треба виводити допоміжну інформацію по регресійному аналізу. Якщо Статистика=1, то допоміжна інформація виводиться, якщо Статистика = 0, то виводяться тільки оцінки коефіцієнтів рівняння.

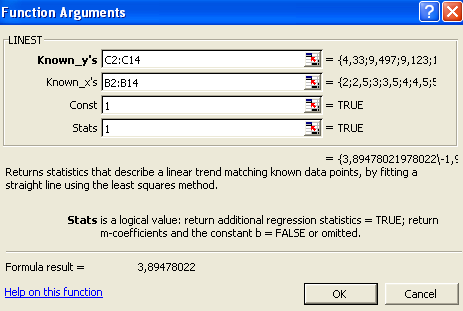
• В лівій верхній комірці виділеної області з’явиться перший елемент підсумкової таблиці. Щоб розкрити всю таблицю, треба нажати <F2>, а далі – комбінацію клавіш <CTRL> + <SHIFT> + <ENTER>.

Допоміжна статистика буде виводитися в такому порядку:

Оцінка параметра а	Оцінка параметра b
Стандартна помилка параметра а	Стандартна помилка параметра b
Коефіцієнт детермінації	Стандартна помилка залежної змінної
F – статистика	Кількість ступенів вільності
Сума квадратів, що пояснює регресію	Сума квадратів помилок

3,89478	-1,90829
0,158042	0,843716
0,98221	1,066054
607,3214	11
690,2037	12,50119

Проаналізуйте ці результати і порівняйте їх з результатами рішення задачі.

Для наочного уявлення одержаних розрахунків на окремому листі будуємо графіки фактичних даних (y), лінії регресії для базисних даних та прогнозу (y_r), довірчу зону для базисних даних і прогнозу (g_y_min, g_y_max), коефіцієнта еластичності (К_ел).

П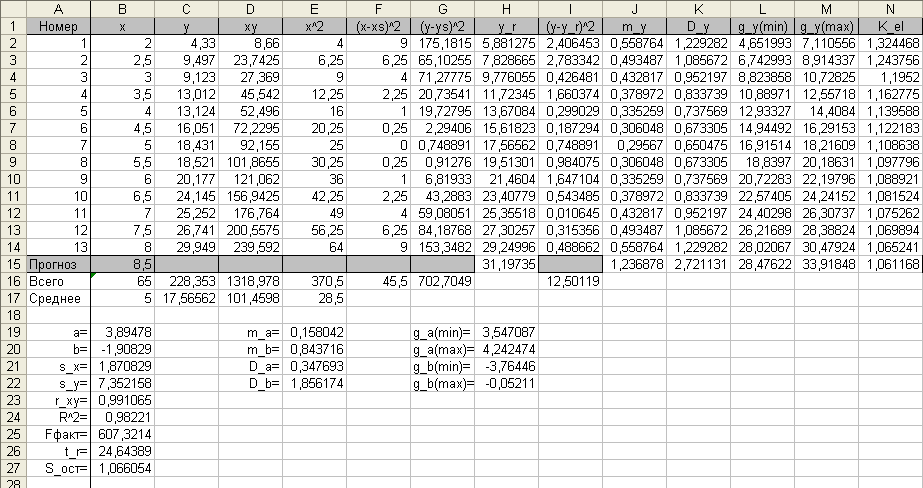 римітка: звернути увагу на фактор х, якщо дані не відсортовані, то передусім відсортувати їх разом з усіма відповідними стовпчиками на окремому листі.

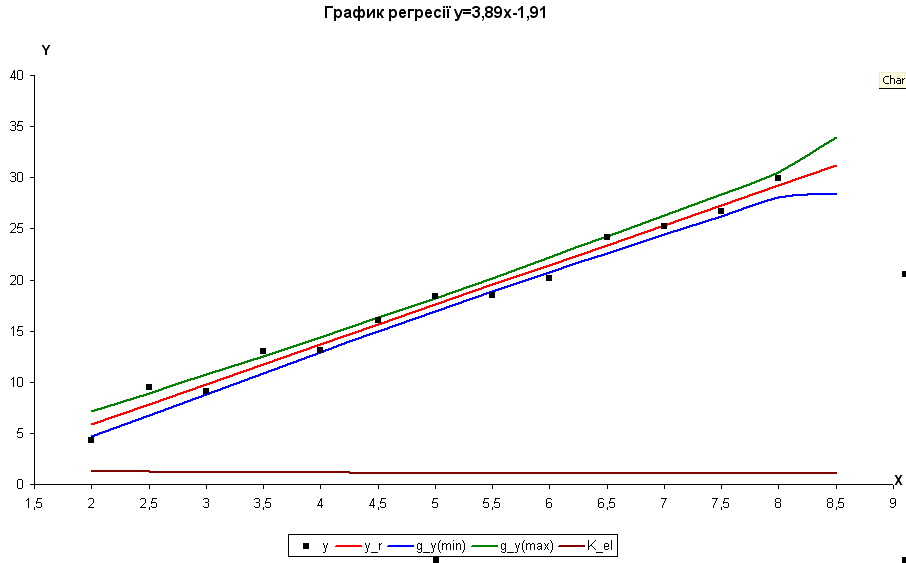
Далі на окремому листі по кожному пункту роботи треба зробити аналіз та економічні висновки.

• пояснюючим фактором.

2.3. Оцінка якості лінейної функції

1.Для оцінки якості підбора лінійної функції розрахували й коефіцієнт детермінації. У нашому випадку коефіцієнт детермінації R²=0.96, що говорить про високу якість побудованої моделі. У такий спосіб рівняння регресії пояснює на 96 % варіацій фактору Х, а на частку основних факторів доводиться 4 %.

2. Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використовують критерій Фішера, з рівнем значимості α=0.05 (тобто ймовірністю P=1-α=1-0.05=0.95). Висуваємо гіпотезу H₀ про статистичну не значимість отриманого рівняння регресії ŷ=1,87Х + 6,16. Розрахуємо F_факт=308,37, F_табл=4,67 (при n=15 й α=0.05). F_факт=308,37 > F_табл=4,67, отже відхиляється гіпотеза про статистично незначущих параметрах рівняння регресії. Дану економетричну модель можна вважати адекватною експериментальним даним з імовірністю Р=0.95. На підставі прийнятої моделі можна проводити економетричний аналіз.

3. Для оцінки статистичної значимості коефіцієнта кореляції використовуємо – критерій Ст’юдента. Висуваємо гіпотезу Н₀ про випадковий характер коефіцієнта кореляції. У нашому випадку Т-крітерій Ст’юдента при рівні значимості α=0.05 (тобто ймовірністю P=1-α=1-0.05=0.95):

t_факт=17,56; t_табл=2,16

t_факт=17,56 > t_табл=2,16 , отже гіпотеза Н₀ – відхиляється, тобто отриманий коефіцієнт rxy не випадково відрізняється від 0, а статистично значимий.

4. а) Перевіримо статистичну значимість коефіцієнта регресії. У нашому випадку а=1,87. Його інтервал довіри має вигляд γ_а=(1,64;2,09). Обидві границі інтервалу довіри мають один знак більше 0. Це говорить про те, що коефіцієнт кореляції регресії а=1,87 не випадково відрізняється від 0.

Перевіримо статистичну значимість вільного члена. У нашому випадку b=6,16. Обидві границі о інтервалу довіри мають знак більше 0 (4,54;7,78). Це говорить про те, що рівняння регресії буде мати вигляд ŷ=1,87Х + 6,16.

б) З імовірністю Р= 0.95 оцінимо інтервали довіри базисних даних. У нашому випадку Хср=6,7, при Х→Х, m_y ( середня стандартна помилка) повинна мати мінімальне значення. Дійсно в нашому випадку при X=6,91, m_y =0,24. У свою чергу на границях інтервалу середня стандартна помилка повинна мати максимальне значення.

При X₁=3,65, m_y=0,402 і при X₁₅=10,72, m_y=0,451, що підтверджується графічно.

в) Розрахуємо прогноз показника і його інтервали довіри. При X_p=10,05, значення отриманої регресії складе ŷ=1,87*10,05 + 6,16. Інтервали довіри для прогнозного значення регресії мають вигляд: (22,75;27,13). Гранична помилка прогнозу, що в 95-процентному випадку не буде перевищена й складе 2,19.

г) Коефіцієнт еластичності прогнозу рівний К_ел=0,75 показує, що при зменшенні фактору на 1% показник зміниться на 0,75 %. Середнє значення коефіцієнта еластичності даної економічної моделі становить К_{ел ср}=0,65. Це говорить про те, що при зміні фактору Х на 1% середнє значення показника зміниться на 0,65 %, що говорить про еластичність моделі.

5. За допомогою стандартної функції ЛИНЕЙН перевіримо розрахункові дані.

Оцінка параметра а	1,868585	Оцінка параметра b	6,158884
Стандартна помилка параметра а	0,106409	Стандартна помилка параметра b	0,751154
Коефіцієнт детермінації	0,959548	Стандартна помилка залежної змінної	0,918571
F-статистика	308,3679	Кількість ступенів вільності	13
Сума квадратів, що пояснює регресію	260,1921	Сума квадратів помилок	10,96903

1,868585	6,158884
0,106409	0,751154
0,959548	0,918571
308,3679	13
260,1921	10,96903