Проверка гипотезы о значимости коэффициента корреляции.

О статистической взаимосвязи говорят, что она существует или отсутствует, имеет направление и характеризуется силой.

Если в результате исследования нулевая гипотеза не отвергается, то «взаимосвязи нет» . В случае, когда нулевая гипотеза отклоняется говорят о существовании связи исследуемых случайных величин.

1. Сформулируем гипотезы H₀ и H₁:

H₀: r =0 (корреляции нет),

H₁: r ≠0.

2. З ададим уровень значимости α.

3. Статистика критерия

Где t-статистика, имеющая распределение Стьюдента с (n-2) степенями свободы.

5. При │t│≥ t_α,n-2 , H₀ отвергается. Это значит, что между параметрами существует значимая корреляция.

При │t│< t_α,n-2 , H₀ принимается.

Пример 1. Результаты измерения величин и даны в таблице

	-2	0	1	2	4
	0,5	1	1,5	2	3

Предполагая, что между и существует линейная зависимость , способом наименьших квадратов определить коэффициенты и .

Решение. Здесь n=5

и нормальная система (*) имеет вид

Решая эту систему, получим: .

Поэтому .

Пример 2. Имеется выборка из 10 наблюдений роста в см. отцов ( ) и их взрослых сыновей ( ).

	180	172	173	169	175	170	179	170	167	174
	186	180	176	171	182	166	182	172	169	177

Требуется найти выборочное уравнение регрессии на . Построить выборочную линию регрессии на .

Решение. 1. Проведем упорядочивание данных по значениям и . Получаем новую таблицу:

	167	169	170	170	172	173	174	175	179	180
	169	171	166	172	180	176	177	182	182	186

2. Для упрощения вычислений составим расчетную таблицу, в которую занесем необходимые численные значения.

167	169	27 889	28 223
169	171	28 561	28 899
170	166	28 900	28 220
170	172	28 900	29 240
172	180	29 584	30 960
173	176	29 929	30 448
174	177	30 276	30 798
175	182	30 625	31 850
179	182	32 041	32 578
180	186	32 400	33 480

Согласно формуле (2), вычисляем коэффициента регрессии,

,

а по формуле (3)

.

Таким образом, выборочное уравнение регрессии имеет вид

.

Н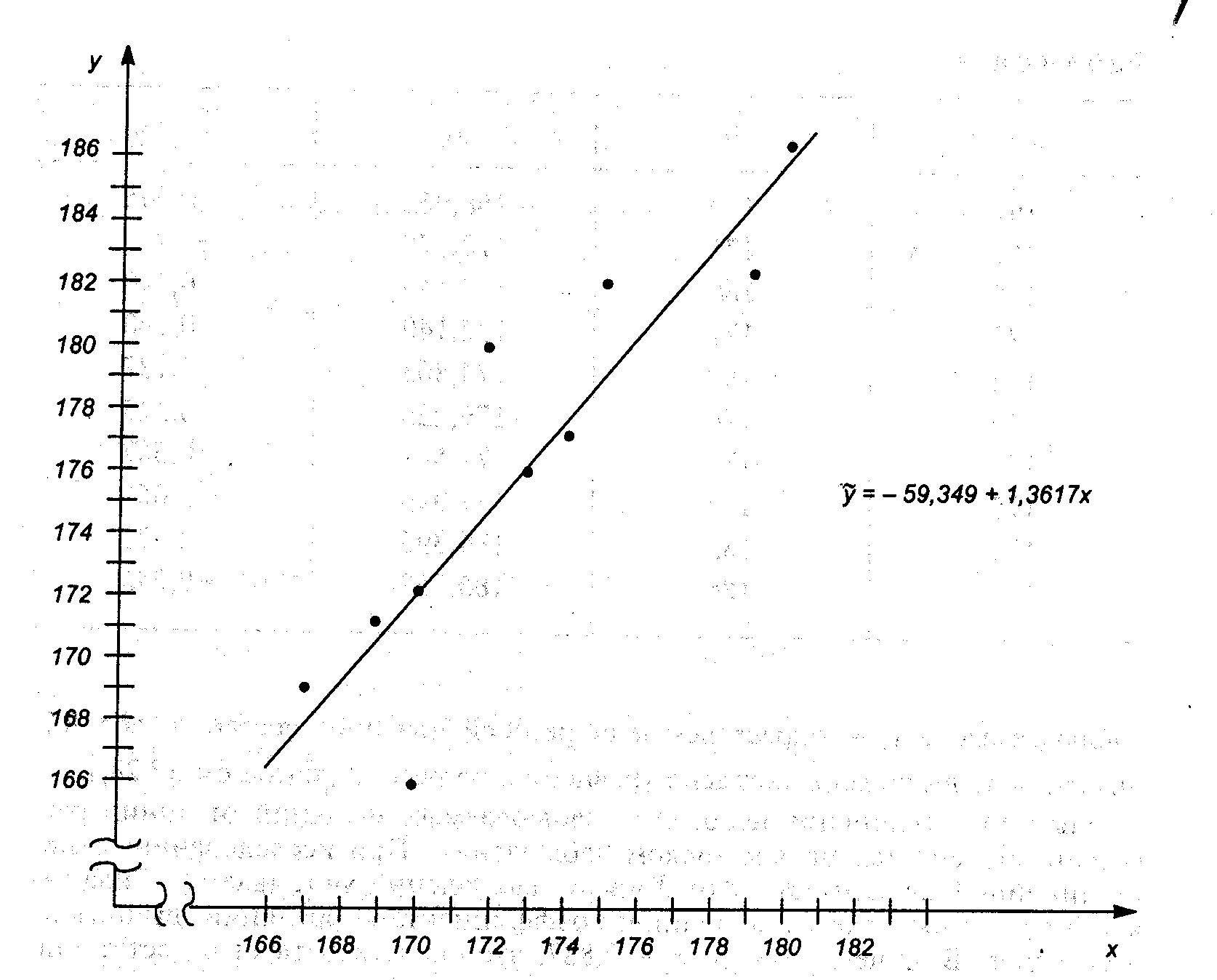 анесем на координатной плоскости точки ( ) и отметим прямую регрессии.

Р

y= -59,349+1,3804x

ис. 4

На рис.4 видно, как располагаются наблюдаемые значения относительно линии регрессии. Для численной оценки отклонений от , где наблюдаемые, а определяемые регрессией значения, составим таблицу:

			-
167	169	168,055	-0,945
169	171	170,778	-0,222
170	166	172,140	6,140
170	172	172,140	0,140
172	180	174,863	-5,137
173	176	176,225	0,225
174	177	177,587	0,587
175	182	178,949	-3,051
179	182	184,395	2,395
180	186	185,757	-0,243

Значения вычислены согласно уравнению регрессии.

Заметное отклонение некоторых наблюдаемых значений от линии регрессии объясняется малым числом наблюдений. При исследовании степени линейной зависимости от число наблюдений учитывается. Сила зависимости определяется величиной коэффициента корреляции.

Пример 3. Вычислить коэффициент корреляции между показателями охвата населения прививками Х (%) и заболеваемостью брюшным тифом (в %). Проверить значимость полученного результата при уровне значимости .

Районы	A	B	C	D	E	F	G	H	I
X	14,7	13,4	9,6	8,1	5,5	5,2	4,4	4,4	4,0
Y	1,4	1,4	2,3	2,1	6,2	6,9	8,6	10,8	11,0

Решение.

Итак,

.

Проверим значимость полученного результата:

По формуле (6) найдем экспериментальное значение критерия

По таблице приложения 2 при уровне значимости и числе степеней свободы находим соответствующее критическое значение .

Мы получили значение , оно больше критического , следовательно, мы отвергаем гипотезу о незначимости коэффициента корреляции, следовательно, между показателями охвата населения прививками и заболеваемости брюшным тифом существует значимая корреляционная связь. Причем поскольку мы можем утверждать, что между этими показателями существует сильная обратная корреляция, т.е., чем больше население охвачено прививками, тем меньше показатель заболеваемости брюшным тифом.

Задания.

1. У окуня озера Баторино измерены длина головы Х и длина грудного плавника У:

Х 66 61 67 73 51 59 48 47 58 44 41 54 52 47 51 45

У 38 31 36 43 29 33 28 25 36 26 21 30 28 27 28 26

Проведите корреляционно-регрессионный анализ полученных данных.

2. Надо было установить, есть ли корреляция между высотой головы Х и длиной 3-го членика усика У у Drosophila funebris. Для этого с ромощью окуляр-микрометра получены следующие данные по Х и У (в делениях окуляр-микрометра):

Х 15 16 15 16 17 18 17 17 15 16 15 17 13 14 17 16 15 16 16 15 18 17 14 15

У 29 31 33 32 33 36 35 35 35 33 31 35 30 31 35 33 32 33 33 30 34 34 31 33

Проведите корреляционно-регрессионный анализ полученных данных.

Литература.

1. Ю.В. Морозов. Основы высшей математики и статистики, М., «Медицина», 2001г.

2. И.В. Павлушков и др. Основы высшей математики и математической статистики, М., Издательский дом ГЭОТАР-МЕД, 2003г.

3. В.Е. Гмурман Теория вероятностей и математическая статистика М., «Высшая школа», 2003г.

4. В.Е. Гмурман Руководство к решению задач по теории вероятностей и математической статистики, М., «Высшая школа», 2003г.

11