Генеральная средняя

Определение. Генеральной средней называют среднее арифметическое значение признака генеральной совокупности:

,

где N - объем совокупности.

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема п.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности:

, или .

х_i – варианта выборки, п_i – частота варианты х_i, - объем выборки.

Рассмотрим некоторую совокупность, значений количественного признака Х объема п:

Значение признака	х1	х2	…	хк
Частота	п1	n2	…	пк

причем .

Отклонением называют разность между значением признака и общей средней.

Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю

.

Генеральная дисперсия

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику – генеральную дисперсию.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:

.

Более удобна формула:

Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:

.

Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выброчной дисперсии:

.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

.

Оценка характеристик положения

Наиболее распространенными опенками характеристик положения являются среднее арифметическое выборки (выборочное среднее), выборочная медиана и выборочная мода. В дальнейшем будем, опускать термин «выборочная», имея, однако, в виду, что любая оценка, начисляемая по выборке, является всего лишь приближенным значением соответствующей характеристики генеральной совокупности

В качестве меры относительного разброса данных используют коэффициент вариации

или

Величину отклонения выборочного показателя (статистики) от его генерального пара­метра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной). Так, стандартная ошибка среднего арифметиче­ского может быть найдена по формуле:

Доверительный интервал

По известным точечным выборочным характеристикам можно построить интервальную оценку или доверительный интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о гене­ральных параметрах на основании известных выборочных показателей, называют доверитель­ными. Обычно в медико-биологических исследованиях приемлемым является значение довери­тельной вероятности Р=0,05 (95%). При этом вероятность выхода истинного значения парамет­ра за пределы этих границ не превышает 1-0,95=0,05 (5%). Величину, дополняющую довери­тельную вероятность да единицы, обычно обозначают α.

Как известно из центральной предельной теоремы, независимо от распределения исход­ной совокупности, из которой извлечены выборки, выборочные средние имеют приближенно нормальное распределение. Таким образом, доверительный интервал для выборочного среднего значения находится между границами и , где - стандартная ошибка среднего, - коэффициент Стьюдента, величина, зависящая от объема выборки (или соответствующего числа степеней свободы ) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента. Величина коэффициента , определяется по таблице на уровне α, дополняющем доверительную вероятность до 1,т.е. в случае 95% доверительного ин­тервала на уровне (1 -0,95) = 0,05 с учетом симметрии интервала.

Нормальное распределение и его параметры.

Нормальное распределение впервые было найдено Абрахамом де Муавром в первой половине XVIII в. (1733г). Затем в начале XIX в. было использовано в работах Гаусса и Лапласа и, по существу, было открыто заново. Под влиянием классических работ Гаусса и Лапласа долгие годы считалось непререкаемой истиной, что все возможные распределения при достаточно большом количестве наблюдений приближаются к нормальному распределению, как некоему идеалу. Подобное утверждение, безусловно, слишком смелое, но тем не менее множество биологических и медицинских показателей, таких как показатели физического развития (вес, рост, давление, температура тела, уровень гормонов), составляющие плазмы крови, демографические и другие показатели следуют нормальному распределению.

Нормальное распределение представляет собой семейство кривых. Каждая кривая это колоколообразный график, на котором по горизонтальной оси откладывается величина эффекта, а на вертикальной – количество пациентов, у которых наблюдался эффект данной величины.

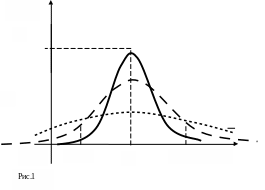
Кривая полностью определяется двумя параметрами, средним и среднеквадратическим отклонением. Факт указанного распределения записывают таким образом: .

Основные характеристики нормального распределения:

- равенство числовых характеристик (среднее, мода и медиана равны между

собой);

- симметричность отклонений от среднего значения;

- общая площадь под кривой равна 1;

- хвосты кривой в обоих направлениях уходят в бесконечность, непрерывно приближаясь, но,

никогда не касаясь, горизонтальной оси, т.е. хвосты асимптотически стремятся к

горизонтальной оси;

- форма кривой определяется среднеквадратическим отклонением генеральной совокупности;

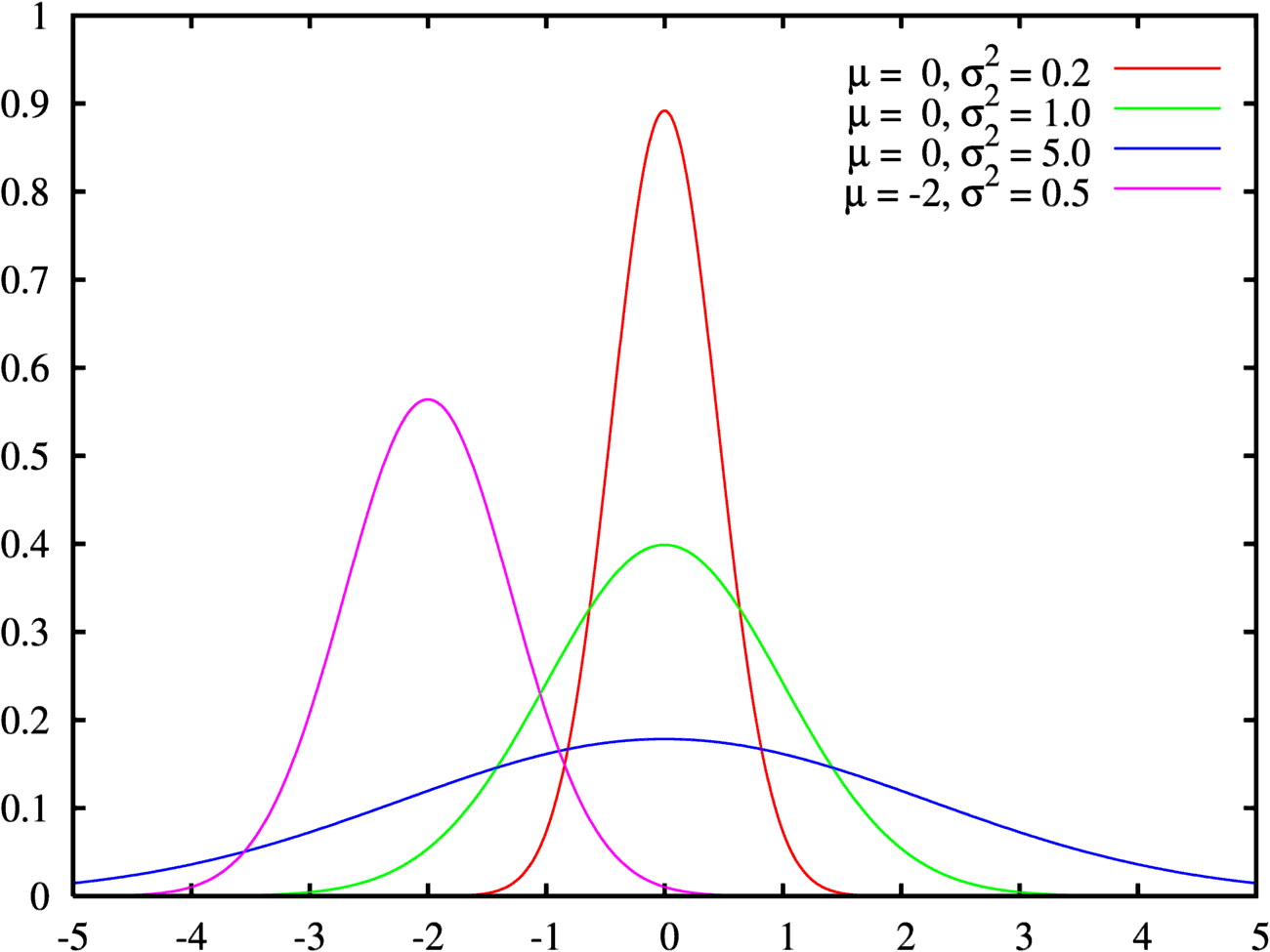
- распределениям с малыми среднеквадратическими отклонениями соответствуют узкие,

вытянутые вверх кривые, а распределениям с большими среднеквадратическими отклонениями

более пологие кривые с менее выраженными вершинами (малые отклонения более вероятны,

большие- менее вероятны);

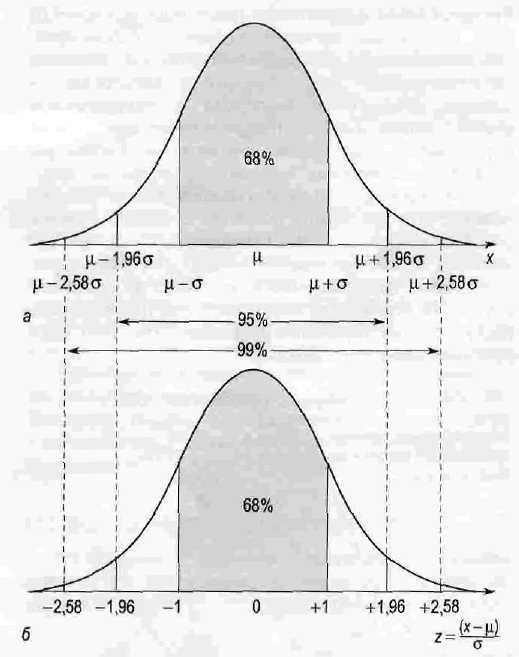
Правило 3-х сигм

68,25% всех значений лежит в интервале ±σ (±1 среднеквадратическое отклонение от среднего);

95,44% всех значений лежит в интервале ±2σ (±2 среднеквадратических отклонений от среднего);

99,73% всех значений лежит в интервале ±3σ (±3 среднеквадратических отклонений от среднего).

Пример. Из очень большой партии ампул извлечена случайная выборка объема 50 интересующий нас признак Х-длины ампул, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 24, 26, 26, 27, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти дискретный , интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).

Решение. Дискретный статистический ряд распределения

	22	24	26	27	28	31	32	33	34	35	36	37	38	40	41	43	44	45	47	50
	1	1	2	1	2	3	2	4	5	2	5	6	2	5	2	1	2	2	1	1
	0,02	0,02	0,04	0,02	0,04	0,06	0,04	0,08	0,1	0,04	0,1	0,12	0,04	0,1	0,04	0,02	0,04	0,04	0,02	0,02

Мода М₀=37.

Медиана

Выборочная средняя

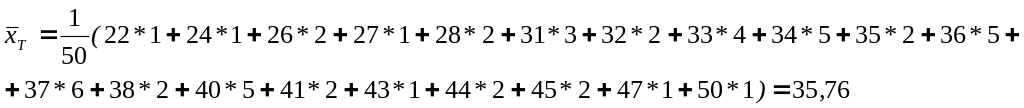
Выборочная дисперсия

Выборочное среднее квадратическое отклонение: .

Величину отклонения выборочного показателя (статистики) от его генерального пара­метра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной):

доверительный интервал для выборочного среднего значения находится между границами и , где - стандартная ошибка среднего, - коэффициент Стьюдента, величина, зависящая от объема выборки (или соответствующего числа степеней свободы ) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента.

Интервальный статистический ряд распределения

Определим количество интервалов по формуле Стерджеса.

,

Определим величину шага интервала h

, =22+4і, і=0,1,…,7.

Интервалы группировки
Частоты	2	5	9	18	9	5	2
Отн.частоты	0,04	0,1	0,18	0,36	0,18	0,1	0,04

Гистограмма частот

4,5

0

22

26

30

34

38

42

46

50

x

2,25

1,25

0,5

Гистограмма относительных частот

0

22

26

30

34

38

42

46

50

x

0,04

0,1

0,18

0,36

Правило 3-х сигм.

• 68,25% всех значений лежит в интервале ±σ (±1 среднеквадратическое отклонение от среднего);

• 95,44% всех значений лежит в интервале ±2σ (±2 среднеквадратических отклонений от среднего);

• 99,73% всех значений лежит в интервале ±3σ (±3 среднеквадратических отклонений от среднего).

, т.е. в интервале расположено 36 вариант из 50.

,

.

Согласно этим данным можно сделать вывод, что выборка распределена нормально.

10