Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра вычислительной техники

и инженерной кибернетики

Лабораторная работа № 4

Вариант № 20, 5555

по дисциплине «Информатика»

И.И. Иванов

Выполнил студент гр. МТ-10-01 ________________ _________________________

подпись, дата инициалы, фамилия

М.Ю. Серебрякова

Принял преподаватель ________________ _________________________

подпись, дата инициалы, фамилия

Уфа 2011

Постановка задачи

Разработать программу получения и обработки одномерного массива, состоящую из 4 частей.

Часть 1. Вычислить значения 33 элементов одномерного целочисленного массива r в интервале (-7,6) с использованием генератора случайных чисел.

Для получения целого случайного числа x на отрезке [a, b] в языке Паскале используется следующий оператор:

x := a + ROUND((b-a)*RANDOM (100)/100).

Чтобы при каждом новом запуске программы получить новую последовательность случайных чисел, необходимо в начале программы исполнить оператор RANDOMIZE.

Часть 2. Вычислить среднегеометрическое значение четных по номеру элементов второй половины массива.

Среднегеометрическое значение ненулевых элементов заданного массива A = {a₁, a₂, a₃, …, a_n} вычисляется по формуле

где К-количество ненулевых элементов в массиве.

Часть 3. Определить наименьший по модулю элемент среди не принадлежащих отрезку [a/2;b/2] элементов второй трети массива.

Определить элемент массива – это значит найти его положение (индекс) в массиве и его значение. Если требуемому условию удовлетворяют несколько элементов, то нужно установить индекс и значение каждого из них.

Часть 4. Упорядочить не отрицательные элементы третьей четверти массива по убыванию обратных значений.

В исходном массиве упорядочиваются только те элементы, которые удовлетворяют заданным условиям, при этом остальные элементы своё положение сохраняют и вспомогательный массив не используется.

Для проверки правильности упорядочения всего массива или его части выводить все его элементы.

Обязательные требования к программе.

1. Программу разработать для решения задачи в общем виде, для произвольных значений исходных данных: количества элементов n (2<=n<=100) и отрезка [a, b] (b>=a).

2. Решение каждой части в программе реализовать в виде процедуры.

3. Предусмотреть 3 варианта исполнения программы:

Тестовый расчёт

Решение задачи для одной и той же последовательности случайных значений элементов массива при новом запуске программы для одних и тех же исходных данных ( Randomize не используется).

Решение задачи для новой последовательности случайных значений элементов массива при новом запуске программы (c Randomize).

1. Анализ задачи.

Исходными данными являются значения количества элементов в массиве n и отрезок [a, b].

Порядок решения задачи: сначала нужно получить одномерный маасив (часть 1), затем можно вычислить параметр массива (часть 2) или найти нужный элемент (часть 3). Упорядочение массива (часть 4) нужно выполнить в последнюю очередь, так как перестановка элементов массива при упорядочении может повлиять на вычисление параметра массива и определение нужного элемента.

Для лучшего понимания задачи, выявления её особенностей выполним тестовый расчёт.

Возьмём любые исходные данные, например n=17, а =-3, в = 4. Запишем 17 случайных целых чисел от -3 до 4 – это значения элементов массива R для тестового расчёта.

1, 0, -3, 2, 0, -3, 4, 3, 2, 0, 0, 4, 0, -2, -1, -1, 1

Для вычисления среднегеометрического значения сначала нужно выделить в общем виде номера элементов второй половины. Номер первого элемента второй половины вычисляется по формуле [n/2]+1 (квадратные скобки обозначают операцию выделения целой части значения выражения. Использование данной операции при определении номеров элементов в большинстве случаев позволяет равномерно разделить массив на части): [17/2] + 1 = [8,5] + 1 = 8 + 1 = 9.

Запишем элементы второй половины

x₉ x₁₀ x₁₁ x₁₂ x₁₃ x₁₄ x₁₅ x₁₆ x₁₇

2 0 0 4 0 -2 -1 -1 1

Выделим подчёркиванием нужные элементы: чётные по номеру, ненулевые значения.

Нужных элементов к = 3, их произведение 4*(-2)*(-1) = 8. Среднегеометрическое значение S_g = .

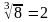При вычислении S_g могут возникнуть следующие проблемы:

1. Не будет нужных элементов ( к = 0 ), например, если все чётные по номеру элементы равны 0. В этом случае нужно принять S_g = 0.

2. Потребуется извлечь корень чётной степени из отрицательного значения произведения ( например, если x₁₆ = 1 ). Это некорректная операция, нужно принять S_g = 0.

Выявленные возможные проблемы нужно учесть при разработке алгоритма.

Можно записать математическую формулировку задачи данной части:

где: k – количество нужных (четных по номеру, ненулевых) элементов во второй половине массива R; 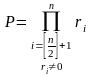- произведение нужных элементов.

Для определения наименьшего элемента сначала выделим элементы второй трети массива: номер первого элемента второй трети [n/3] + 1 = [17/3]+1 = [5,66] + 1 = 5 + 1 = 6, номер последнего [2*n/3] = [2*17/3] = [34/3] = [11,33] =11.

Запишем элементы второй трети массива:

x₆ x₇ x₈ x₉ x₁₀ x₁₁

-3 4 3 2 0 0

Выделим подчёркиванием нужные элементы: не принадлежащие отрезку [a/2,b/2] для a = -3, b = 4. Нужных элементов 3, наименьшее по модулю значение равно 3, такое значение имеют два элемента: x_{6 =} -3 и x₈ =3.

При решении данной задачи могут быть следующие ситуации:

1. Не будет нужных элементов;

2. Будет единственный элемент с наименьшим значением;

3. Будет множество элементов с наименьшим значением (в пределе все нужные элементы в рассматриваемой части имеют одинаковое значение).

При выборочном упорядочивании элементов массива сначала выделим нужную часть массива. Первый элемент третьей четверти массива имеет номер [n/2] + 1 = [17/2] +1 = [8,5] +1 = 8 + 1 = 9, последний элемент имеет номер [3*n/4] = [3*17/4] = [51/4] = [12,75] = 12.

Запишем элементы третьей четверти

Элементы x₉ x₁₀ x₁₁ x₁₂

Значения элементов 2 0 0 4

Обратные значения 0,5 ∞ ∞ 0,25

Упорядоченные элементы 0 0 2 4

Все элементы неотрицательны – равны 0 или больше 0, поэтому все элементы второй трети меняют своё положение в массиве.

При разработке алгоритма возникает проблема вычисления обратного значения для элементов равных нулю – деление на ноль недопустимо. Для решения этой проблемы нужно математическую _∞ заменить очень большим положительным числом – «машинной бесконечностью», например 10³⁶. Для этого в алгоритме условие вида 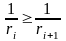нужно заменить на

Тогда при вычислении обратного значения деления на ноль не будет, а на сравнение значений, отличных от нуля такое слагаемое не повлияет.