
- •Введение Металингвистические формулы
- •Простейшие приемы программирования. Оператор присваивания.
- •Разветвления
- •Простейшие циклы
- •Целочисленная арифметика
- •Сочетание цикла и разветвления
- •Вычисления с заданной точностью
- •Использование перечислений. Многозначное ветвление
- •Вычисления с хранением последовательности значений. Одномерные массивы
- •Вложенные циклы.
- •Вложенные циклы в матричных задачах.
- •Дана действительная квадратная матрица . Получить две квадратные матрицы, , , для которых
- •Обработка последовательностей символов
- •Геометрия
- •Многочлены
- •Использование комбинированных типов Использование подпрограмм
- •Рекурсия Файлы
- •Сортировка массивов и файлов Системы счисления Связное представление данных в памяти
- •Двоичные деревья
- •Примерные варианты контрольных работ Контрольная работа №1
Использование перечислений. Многозначное ветвление
Вычисления с хранением последовательности значений. Одномерные массивы
Даны действительные числа
 ,
,
 ,
…,
,
…,
 количество осадков
(в миллиметрах), выпавших в Москве в
течение первых 50 лет предыдущего
столетия. Надо вычислить среднее
количество осадков и отклонение от
среднего для каждого года.
количество осадков
(в миллиметрах), выпавших в Москве в
течение первых 50 лет предыдущего
столетия. Надо вычислить среднее
количество осадков и отклонение от
среднего для каждого года.Система из 25 материальных точек в пространстве задана с помощью последовательности действительных чисел
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
…,
,
…, ,
,
 ,
,
 ,
,
 ,
где
,
где
 ,
,
 ,
,
 координаты
координаты
 -ой
точки, а
-ой
точки, а
 ее вес (
ее вес ( ).
Получить координаты центра тяжести
системы, а также расстояния от центра
тяжести до всех точек системы.
).
Получить координаты центра тяжести
системы, а также расстояния от центра
тяжести до всех точек системы.Построить последовательность целых чисел , , …, , где
 ;
;
 ;
;
 (
( ).
).Даны действительные числа , , …, . Получить ,
 ,…,
.
,…,
.Даны действительные числа , , …, , , , …,
 .
Вычислить
.
Вычислить
 .
.Даны действительные числа , , …,
 ,
,
,
…,
,
,
,
…,
 .
Члены последовательности
,
,
…,
.
Члены последовательности
,
,
…,
 связаны с членами данных последовательностей
соотношениями
связаны с членами данных последовательностей
соотношениями
 ,
,
 (
( ).
Получить
,
,
…,
.
).
Получить
,
,
…,
.Даны действительные числа , , …,
 .
Получить:
.
Получить:,
 ,
,
,
,
 …,
,
;
…,
,
;, , ,
 ,…,
,
;
,…,
,
; ,
,
 ,…,
,…,
 .
.
Даны действительные числа , , …,
 .
Получить:
.
Получить:, , , …,
 ;
; ,
,
 ,
…,
,
,
,
…,
,
…,
,
,
,
…,
 ;
;, , …, , ,
 ,
…,
.
,
…,
.
Даны действительные числа , , …,
 .
Получить:
.
Получить:, ,
 ,
,…,
,
;
,
,…,
,
;,
 ,…,
,
,
,…,
,
,
 ,…,
;
,…,
;, , ,
 ,…,
,
;
,…,
,
;, ,
 ,
,…,
,
;
,
,…,
,
;, , , , , , , ,…, , , , .
Даны действительные числа , , …, . Если в результате замены отрицательных членов последовательности , , …, их квадратами члены будут образовывать неубывающую последовательность, то получить сумму членов исходной последовательности; в противном случае получить их произведение.
Даны целые числа , , …,. Все члены последовательности с четными номерами, предшествующие первому по порядку члену со значением
 ,
умножить на
.
,
умножить на
.Даны целые числа , , …,. , каждое из которых отлично от нуля. Если в последовательности отрицательные и положительные члены чередуются, то ответом должна служить сама исходная последовательность. Иначе получить все отрицательные члены последовательности, сохранив порядок их следования.
Даны натуральное число , действительные числа , , …,
 (числа
,
,
…,
попарно различны,
(числа
,
,
…,
попарно различны,
 ).
В последовательности
,
,
…,
поменять местами больший член и член
с номером
.
).
В последовательности
,
,
…,
поменять местами больший член и член
с номером
.Даны действительные числа , …,
 ,.
,
…,
,.
,
…,
 .
Получить действительные
.
Получить действительные
 ,
…,
,
…,
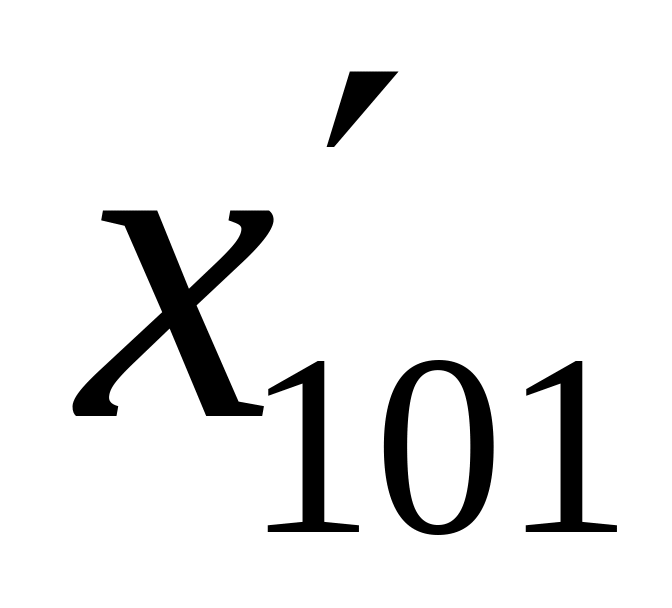 ,.
,. ,
…,
,
…,
 ,
преобразовав для получения
,
преобразовав для получения
 ,
,
 члены
,
по правилу: если они оба отрицательны,
то каждый из них увеличить на 0.5; : если
отрицательно только одно число, то
отрицательное число заменить его
квадратом; если оба числа неотрицательны,
то каждое из них заменить на среднее
арифметическое исходных значений.
члены
,
по правилу: если они оба отрицательны,
то каждый из них увеличить на 0.5; : если
отрицательно только одно число, то
отрицательное число заменить его
квадратом; если оба числа неотрицательны,
то каждое из них заменить на среднее
арифметическое исходных значений.Даны действительные числа , …, . Получить:
 ;
; .
.
Даны действительные числа , …, . Преобразовать эту последовательность по правилу: большее из
 и (
и ( )
принять в качестве нового значения
,
а меньшее в качестве
нового значения
)
принять в качестве нового значения
,
а меньшее в качестве
нового значения
 .
.Даны целые числа , …, . Если в последовательности ни одно четное число не расположено после нечетного, то получить все отрицательные члены последовательности, иначе все положительные. Порядок следования чисел в обоих случаях заменяется на обратный.
Даны действительные числа
 ,
…,
,
…,
 ,
среди которых заведомо есть как
отрицательные, так и неотрицательные.
Получить
,
среди которых заведомо есть как
отрицательные, так и неотрицательные.
Получить
 ,
где
,
…,
,
где
,
…,
 ,
отрицательные
члены последовательности
,
…,
,
взятые в порядке их следования,
,
…,
,
отрицательные
члены последовательности
,
…,
,
взятые в порядке их следования,
,
…,
 неотрицательные
члены, взятые в обратном порядке,
неотрицательные
члены, взятые в обратном порядке,
 .
.Даны целые числа , …, . Наименьший член последовательности , …, заменить целой частью среднего арифметического всех членов, остальные члены оставить без изменения. Если в последовательности несколько членов со значением
 ,
то заменить последний по порядку.
,
то заменить последний по порядку.Даны действительные числа , …, . (все попарно различны). Поменять в этой последовательности местами:
наибольший и наименьший члены;
наибольший и последний члены.
Даны целые числа , …,
 .
Получить новую последовательность из
100 целых чисел, заменяя
нулями, если
.
Получить новую последовательность из
100 целых чисел, заменяя
нулями, если
 и заменяя
единицей в противном случае (
и заменяя
единицей в противном случае ( ).
).Даны целые числа , …,
 ,
,
…,
,
,
…,
 .
Преобразовать последовательность
,
…,
по правилу: если
.
Преобразовать последовательность
,
…,
по правилу: если
 ,
то
,
то
 увеличить в 10 раз, иначе
заменить нулем (
увеличить в 10 раз, иначе
заменить нулем ( ).
).Даны действительные числа , …,
 .
Требуется умножить все члены
последовательности
,
…,
на квадрат ее наименьшего члена, если
.
Требуется умножить все члены
последовательности
,
…,
на квадрат ее наименьшего члена, если
 ,
и на квадрат наибольшего члена, если
,
и на квадрат наибольшего члена, если
 .
.Дано натуральное число , действительные числа , …,
 .
Получить
,
…,
.
Получить
,
…,
 ,
где
равно сумме тех членов последовательности
,
…,
,
которые принадлежат полуинтервалу
,
где
равно сумме тех членов последовательности
,
…,
,
которые принадлежат полуинтервалу
 (
( ).
Если полуинтервал не содержит членов
последовательности, то соответствующее
положить равным нулю.
).
Если полуинтервал не содержит членов
последовательности, то соответствующее
положить равным нулю.Даны действительные числа , , ,
 ,
,
 ,
,
,
,
 ,…,
,…,
 (
( ).
Пары (
,
),
(
,
),…,(
,
)
рассматриваются как координаты точек
на плоскости. Числа
,
,…,
рассматриваются как радиусы одиннадцати
полукругов в полуплоскости
).
Пары (
,
),
(
,
),…,(
,
)
рассматриваются как координаты точек
на плоскости. Числа
,
,…,
рассматриваются как радиусы одиннадцати
полукругов в полуплоскости
 с центром в начале координат. Найти
количество точек, попадающих внутрь
каждого полукруга (границы-полуокружности
не принадлежат полукругам).
с центром в начале координат. Найти
количество точек, попадающих внутрь
каждого полукруга (границы-полуокружности
не принадлежат полукругам).Даны действительные числа , ,
 ,
принадлежащие полуинтервалу
,
принадлежащие полуинтервалу
 .
Полуинтервал разбивается на 100 равных
частей. Вычислить
,
,
.
Полуинтервал разбивается на 100 равных
частей. Вычислить
,
,
 ,
где
,
где
 ,
а количество
заданных чисел, принадлежащих
полуинтервалу
,
а количество
заданных чисел, принадлежащих
полуинтервалу
 (
( ).
).Даны действительные числа , …, . Переставить члены последовательности , …, так, чтобы сначала расположились все ее неотрицательные члены, а потом все отрицательные. Порядок как среди неотрицательных членов, так и среди отрицательных должен быть сохранен прежним.
