15. Векторное и смешанное произведения векторов.

Векторное произведение векторов

Определение. – вектор, удовлетворяющий трем условиям:

1. ,

2. ,

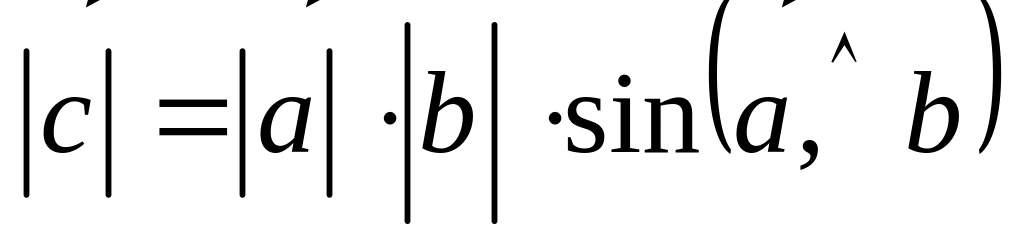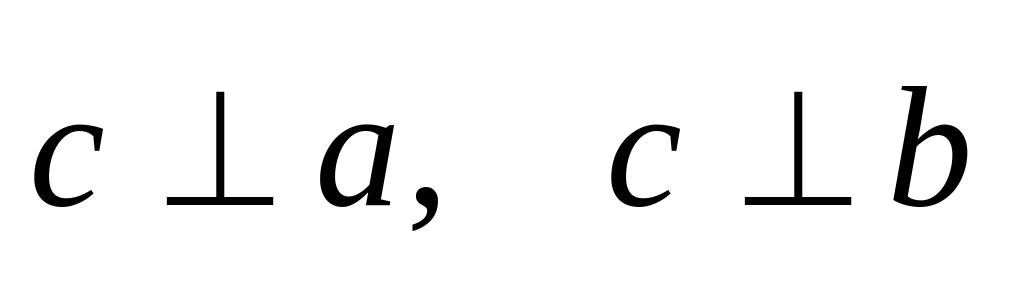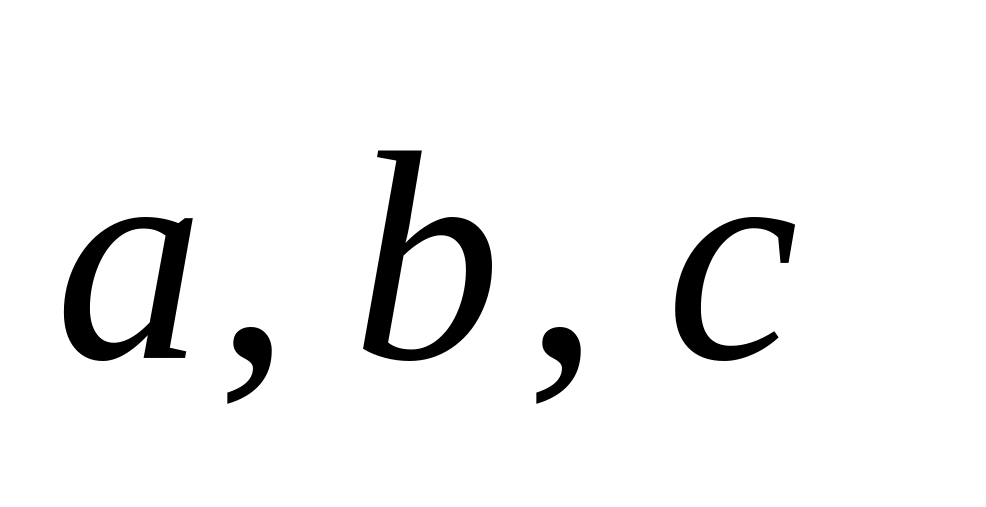3. образуют правую тройку, то есть, если смотреть из конца 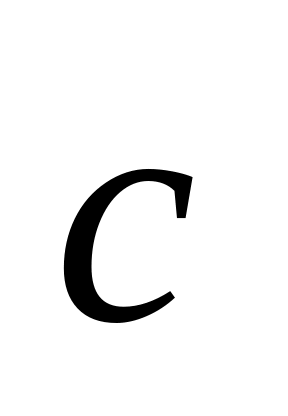, то кратчайший поворот от 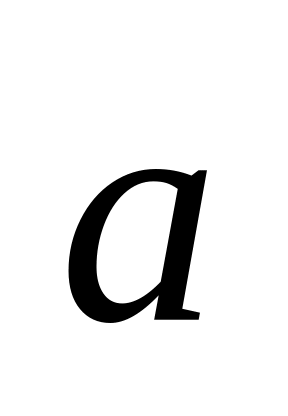к 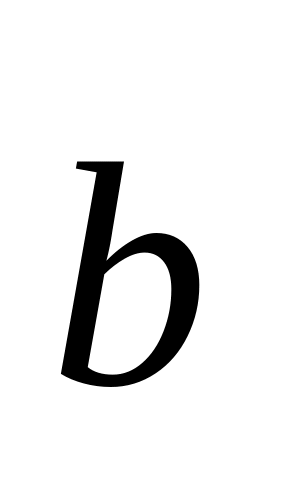виден против часовой стрелки (рис. 3).

З амечание: Если вектор изображает силу, приложенную к точке А, а вектор направлен из некоторой точки О в точку А, то вектор представляет собой момент силы относительно точки О: (8)

Свойства:

1) ,

2) , если , либо , либо || ,

3) ,

4) .

Если известны координаты векторов, то

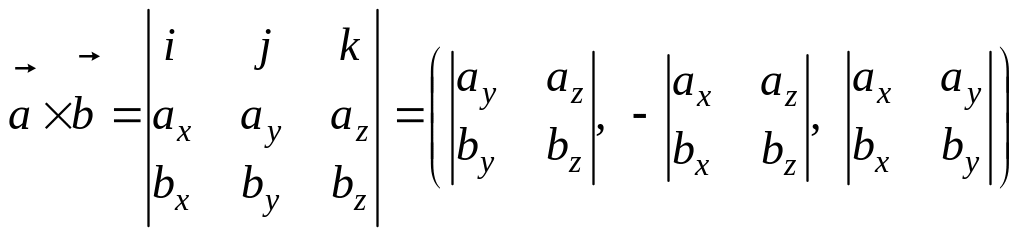(9)

Площадь параллелограмма, построенного на векторах и :

– площадь треугольника (10)

§ 4. Смешанное произведение векторов

Смешанным произведением векторов называют число, равное . Обозначают также .

Если известны координаты векторов, то

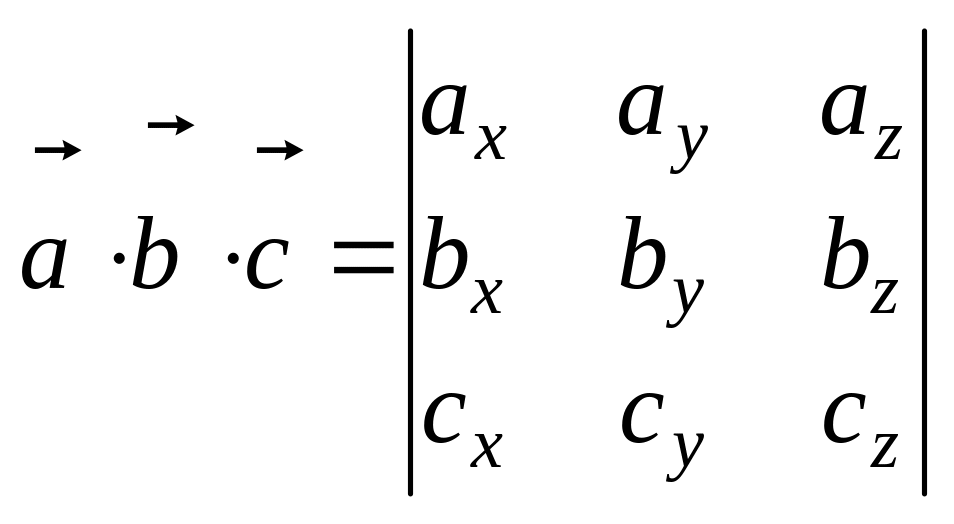
Объем пирамиды равен (11)

§ 5. Аналитическая геометрия на плоскости. Прямая на плоскости

Общее уравнение прямой :

, где . (12)

Уравнение прямой с угловым коэффициентом:

, , , , (13)

где – угловой коэффициент прямой, равный тангенсу угла наклона прямой к оси ; – отрезок, отсекаемый прямой на оси .

– уравнение прямой в отрезках, (14)

г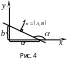 де и – отрезки, отсекаемые прямой на осях и соответственно (рис. 4)

Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору нормали :

(15)

Уравнение прямой, проходящей через заданную точку параллельно заданному направляющему вектору :

(16)

Уравнение прямой, проходящей через две заданные точки и :

(17)

Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом :

(18)

Угол между прямыми и

Если :

: ,

то (19)

Если :

: ,

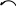то (20)

Замечание.

а) || || или , (21)

б) или (22)

Координаты точки пересечения двух прямых и ищутся как решение системы:

(23)

Расстояние от точки до прямой : ищется по формуле:

16. Способы задания прямой на плоскости. Прямая на плоскости

Общее уравнение прямой :

, где . (12)

Уравнение прямой с угловым коэффициентом:

, , , , (13)

где – угловой коэффициент прямой, равный тангенсу угла наклона прямой к оси ; – отрезок, отсекаемый прямой на оси .

– уравнение прямой в отрезках, (14)

г де и – отрезки, отсекаемые прямой на осях и соответственно (рис. 4)

Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору нормали :

(15)

Уравнение прямой, проходящей через заданную точку параллельно заданному направляющему вектору :

(16)

Уравнение прямой, проходящей через две заданные точки и :

(17)

Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом :

(18)

Угол между прямыми и

Если :

: ,

то (19)

Если :

: ,

то (20)

Замечание.

а) || || или , (21)

б) или (22)

Координаты точки пересечения двух прямых и ищутся как решение системы:

(23)

Расстояние от точки до прямой : ищется по формуле:

(24)