14. Скалярное произведение векторов. Евклидово пространство. Условие ортогональности векторов.

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная илинейная по каждому сомножителю.

Скалярным произведением в векторном пространстве   над полем   комплексных (или   вещественных) чиселназывается функция   для элементов , принимающая значения в   (или  ), определенная для каждой пары элементов и удовлетворяющая следующим условиям:

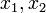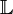1. для любых трех элементов   и   пространства   и любых чисел   из   (или  ) справедливо равенство   (линейность скалярного произведения по первому аргументу);

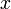2. для любых   и   справедливо равенство 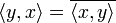 , где черта означает комплексное сопряжение (эрмитова симметричность);

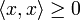3. для любого   имеем  , причем 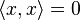  только при 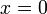  (положительная определенность скалярного произведения).

Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.

Заметим, что из п.2 определения следует, что  . Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.

Евклидовы пространства. Для развития геометрических методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам х и у из R ставится в соответствие число, обозначаемое (х, у) и называемое скалярным произведением векторов х иу. При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения:

         1) (х, у) = (у, х) (перестановочность);

         2) (x₁ + x₂, y) = (x₁, y) + (x₂, y) (распределительное свойство);

         3) (αx, у) = α(х, у),

         4) (х, х) ≥ 0 для любого х, причем (х, х) = 0 только для х = 0.

         Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством (См. Гильбертово пространство). Длина |x| вектора x и угол  х и у евклидова пространства определяются через скалярное произведение формулами

         

         Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство Eⁿ получим, определяя в n-мepном арифметическом В. п. скалярное произведение векторов x = (λ₁, …, λ_n) и y = (μ₁, …, μ_n) соотношением

         (x, y) = λ₁μ₁ + λ₂μ₂ +… + λ_nμ_n. (2)

         При этом требования 1)—4), очевидно, выполняются.

         В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: (х, у) = 0. В рассмотренном пространстве Eⁿ условие ортогональности векторов x= (λ₁, …, λ_n) и y = (μ₁, …, μ_n), как это следует из соотношения (2), имеет вид:

         λ₁μ₁ + λ₂μ₂ +… + λ_nμ_n = 0. (3)