Пример 2.7:
В примере 2.1
y1=x12 y2=8x2 2
имеем a1=1, a2=8, mx=4, my=2. Критерии подобия
П1= x12/ y1, П2=8 x22/ y2
Условие (24)
=
=
=
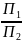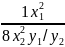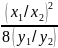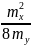= 1
Выполняется. Функции y1 ,y2 подобны.
Итак, для подобия степенных комплексов необходимы и достаточны: их сходственность; связь сходственных переменных масштабами; непротиворечивость (совместность) уравнений, выражающих сходственные степенные комплексы, и уравнения, выражающих масштабы сходственных переменных. Последние условия фактически означают, что масштабы не могут выбираться произвольно, а должны удовлетворять определенному масштабному уравнению вида (24).
Анализ совместности уравнений, выражающих сходственные степенные комплексы и масштабы, заключается в выводе масштабного уравнения и выяснения вопроса, удовлетворяют ли этому уравнению масштабы.
Пример 2.8:
Если в примере 2.7 принять mx=my=4, то масштабное уравнение =1 не удовлетворяется. Функции y1 ,y2 не являются подобными.
Как было показано, масштабное уравнение можно вывести двумя способами, с помощью преобразования одного сходственного уравнения в другое и с помощью критерия подобия.
Всё положенное для простейших степенных комплексов (18), (19) легко распространяются на общий случай (16).
2.4. Подобие в общем виде
Обратимся теперь к ситуации, когда объекты описываются уравнениями общего вида (1), (2). При этом остальные в силе и три необходимых условия подобия. Как и в рассмотренном простейшем случае, масштабные уравнения можно получить двумя способами.
F(y1, x1i, t1j, D1j, A1s)=0 (1)
F(y2, x2i, t2j, D2j, A2s)=0 (2)
my=y1/y2,.. (3)
Способ подстановки основан на преобразовании одного уравнения в другое. Если системы уравнений (1), (2) непротиворечива, то каждое сходственное уравнение можно решить двумя путями: прямым и окольным, согласно схемам на рис. 2.4, аналогичным схемам на рис. 2.3.
y2
y1
(2)
(1)
Замена
y1, x1i, t1j, D1j, A1s
на
y2, x2i, t2j, D2j, A2s
Замена
y2, x2i, t2j, D2j, A2s
на
y1, x1i, t1j, D1j, A1s
(1)
(2)
=
=
=
=
y2*
y1*
(1**)
(2*)
(2**)
(1*)
а)
б)
Рис. 2.4. два пути решения уравнений (1)(а) и (1) (б) в случае их подобия
Прямой путь определения неизвестной функции y1 (рис. 2.4,а) заключается в непосредственном решении уравнения (1), окольный в замене переменных уравнения (2) переменными уравнения (1) согласно (3) и решения уравнения
F(y1/my, x1i/mxi, t1j/mtj,mtj D1j, A1s)=0 (1*)
Замена переменных y2, x2i, t2j сходственными переменными y1, x1i, t1j выполняется согласно соотношениям
y2=y1/my, x2i=x1i/mxi, t2j=t1j/mtj
С помощью тех же масштабов my, mxi, mtj осуществляется замена производных сходственных величин. Масштабы связывают все возможные значения y1, x1i, t1j, D1j, A1s и соответствующие им значения y2, x2i, t2j, D2j, A2s, в том числе и бесконечно малые приращения, т.е. дифференциалы
my=dy1/dy2, mxi=dx1i/dx2i, mtj=dt1j/dt2j
для замены производной D2j y2, сходственной производной D1j y1, находим отношение
=
/
=
=
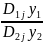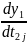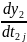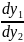
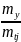(28)
откуда
=
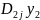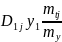(29)
Эти же выражения можно получить формально проще, так как dt2j= dt1j/ mtj, то
D2j=
=
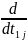mtj=
D1j
m2j
откуда
mtj= D2j / D1j, (30)
что позволяет рассматривать операторы D1j, D2j как сходственные величины, связанные масштабами
mDj=D1j / D2j=1/ mtj
В таком
случае производную D2j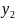
можно рассматривать как обычное
произведение и заменять D2j
на D1j
и y2 на y1
раздельно с помощью масштабов mtj
и my.
При этом
=
=
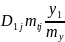, как в (29). Аналогично вторую производную
D22j
можно заменить сходственной второй
производной D21j
:
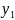D22j = D21j m2tjy1/my= D21j m2tj/my
ч.т.д. Все сказанное легко распространяется на частные и смешанные производные.
Итак, при замене переменных одного уравнения сходственными переменными другого в качестве переменных формально можно рассматривать любые операторы дифференцирования.
После замены переменных y2, x2i, t2j, D2j переменными y1, x1i, t1j, D1j уравнение (2) приводиться к виду (1*), отличающемуся от (21) только постоянными коэффициентами.
В случае подобия решения y1 и y1* уравнений (1) и (1*) тождественны: y1 = y1*
Прямой путь определения неизвестной функции y2 (рис. 2.4, б) состоит в решении (2), окольный – в замене переменных y1, x1i, t1j, D1j уравнения (1) переменными y2, x2i, t2j, D2j согласно (3), (30) и решения уравнения
F(myy2, mxix2i, mtjt2j, D2j/mtj, A2s)=0 (2*)
В случае подобия решения y2 и y2* уравнений (2) и (2*) тождественны: y2 = y2*.(Пример 2.9)
Для выполнения условий y1 = y1* можно не прибегать к аналитическому решению уравнений (1), (1*), что, кстати, не всегда возможно. Для этого достаточно сделать уравнения (1), (1*) равносильными, приравняв их сходственные коэффициенты. Однако в общем случае эти коэффициенты обладают различными размерностями. Поэтому необходимо предварительно преобразовать (рис.2.4, а) уравнение (1*) в уравнение
F(y1, x1i, t1j, D1j, A1s**)=0 (1**)
так, чтобы размерности сходственных коэффициентов (1**) и (1) были одинаковы: [A1s**]=[A1s]. Условия равенства y1 = y1* получаются в виде A1s**=A1s . (Пример 2.10 и 2.11)
Совершенно аналогично получаются масштабные уравнения из условия тождественности (2) и (2*).
Таким образом, сущность способа подстановки состоит: в замене переменных второго уравнения с помощью масштабов; обеспечение тождественности промежуточного уравнения и второго сходственного уравнения; получении масштабных уравнений, как условий тождественности указанных двух уравнений.