Пример 1.2.

Каждый материальный объект обладает несколькими свойствами, допускающими количественные выражения. Каждое свойство характеризуется определенной физической величиной своего размера. Между различными свойствами объективно существуют конкретные связи. Они обусловливают определенные соотношения между размерами физических величин, которые можно выразить в виде формулы. Поэтому, если выбрать произвольно единицы некоторых физических величин, то через эти единицы можно выразить единицы всех остальных физических величин.

Физические величины, размеры единиц которых выбираются произвольно, называют основными. Единицы измерения основных физических величин также называют основными. Единицы измерения всех остальных физических величин выражают через основные и называют производными. Совокупность основных и производных единиц составляет систему единиц измерения.

В международной системе единиц, сокращенно обозначаемой СИ – «система интернациональная», основными физическими величинами является длина, масса, время, сила электрического тока, сила света, количество вещества, температура. Основными единицами этой системы выбраны метр (м), килограмм (кг), секунда (с), ампер (А), кандела (кд), моль (моль), кельвин (К).

Пусть для физических величин y₁, y₂,… выбраны независимые основные единицы {y₁},{ y₂},…

И для другой физической величины x требуется установить производную единицу {x}. Для этого выбирают материальный объект, в котором размеры x, y₁, y₂,… связаны уравнением

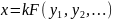(3)

где k – коэффициент пропорциональности, или

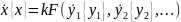(4)

Положив 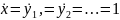, можно выразить производную единицу через основные

(5)

Для обеспечения «согласованности», т. е. идентичности выражений, связывающих размеры и числовые значения x, y₁, y₂,… аналогичной (3) должна быть зависимость

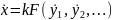(6)

Подставив выражения (5), (6) в (4), получаем уравнение

равносильное системе двух уравнений

(7)

(8)

Алгебраическое уравнение (7) имеет два вещественных корня (0,1). Отбросив первый корень как не имеющий смысла, получим k=1. Уравнение (8) является функциональным, в котором неизвестен вид функции F. по смыслу выражения (3) эта функция должна быть непрерывной. Единственной непрерывной функцией, удовлетворяющей уравнению (8), является произведением степеней y₁, y₂,…, т.е. функция

(9)

В которой показатели степеней могут быть любыми числами и которую называют степенным комплексом.

В результате приходим к важному выводу, что для установления производных единиц измерения пригодны только физические формулы в виде степенных комплексов с постоянным коэффициентом, равным единице. Степенной комплекс, выбранный для установления производной единицы измерения, называется определенным уравнением для этой единицы.

В самом общем случае производная единица {x} физической величины x выражается не только через основные единицы ,… основных физических величин y₁, y₂,…, но и через ранее установленные произвольные единицы ,… других величин x₁, x₂,…, и определяющие уравнения для {x} имеет вид

(10)

После подстановки сюда выражений 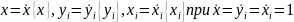получаем общее символическое выражение производной единицы

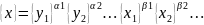(11)

Чем проще определяющее уравнение (10), т.е. чем меньше физических величин связано с этим уравнение, и чем проще связи между ними, тем отчетливее проявляется физический смысл размера произвольной единицы. Поэтому, как правило, определяющее уравнение выбирается так, чтобы оно содержало не более трех – четырех физических величин, а модули степеней α, β были равны единице или двум. (Пример 1.3)

… производную единицу физической величины x можно определить символически в двух формах. Первая выражает производную величину через единицу физических величин определяющего уравнения и раскрывает её физический смысл. По существу она является конкретным представлением размера {x}. Вторая форма выражает производную единицу через основные единицы, не раскрывает её физического смысла, имеет абстрактный характер, но отличается определенной общностью для всех физических величин. Эту форму представления производной единицы называют размерностью и обозначают [x].

Так как размер {x} и размерность [x] выражают по – разному, но одну и ту же единицу измерения, то 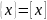(14)

Основная единица обозначается либо символом соответствующей физической величины Y, например единица длины L, единица времени T, либо специальным символом, представляющим сокращенное её название, например единица длины метр – м, единица времени секунда – с. Первое обозначение преимущественно используется в формуле размерностей [y]=Y, второе – при конкретизации единиц физических величин.

Производная единица обозначается при её конкретизации либо, специальным символом, представляющим сокращенное её название {x} = назв., например единицы силы ньютон – н, единица работы джоуль – Дж, либо символом единиц физических величин определяющего уравнения например единица скорости м/с, единица давления н/м². В формулах размерностей используется общее обозначение [x].

Если в правой части определяющего уравнения (10) содержаться только размеры основных физических величин и β₁=β₂=…=0, то согласно (11) 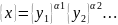(15)

Положив {x}=[x], {y₁}=[y₁], {y₂}=[y₂]…, получим формулу размерности

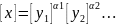(16)

аналогичную (15). Например, для единицы скорости

{v}={l}{t}^-1, [v]=[l][t]^-1

Если в правой части (10) содержаться размеры основных других физических величин, а соответствующие производные единицы

, ,

то, подставив эти выражения в (11), с учетом равенства (14), получим

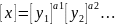(17)

где,

a₁=α₁+α₁₁β₁+ α₁₂β₂+…, a₂=α₂+α₂₁β₁+ α₂₂β₂+…,

Сравнение (17) и (11) показывает, что в общем случае формулы размера и размерности производной единицы различны. Например, для единицы силы в СИ

{F}=кг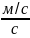 , [F]=LMT^-2

В результате физическое истолкование формул размерности производных единиц часто оказывается невозможным. На основании формулы для [F] можно сказать только, что основными физическими величинами для определения единицы силы приняты длина, масса и время, что размер единицы силы прямо пропорционален размерам единиц длины и массы и обратно пропорционален квадрату размера единицы времени. Представления о конкретных размерах единиц длины, массы, времени, и силы формула не дает. Размерность – это символическое выражение единицы величины, через основные единицы, показывающие соотношение между их размерами без указаний этих размеров. Понятие «размерность», строго говоря, относится к единице измерения физической величины. Однако его распространяют и на физическую величину. Например, говорят о размерности скорости, ускорения, силы вместо того, чтобы говорить только о размерности единиц этих величин. В результате приходят к понятиям размерных и безразмерных величин.

Величина x называется безразмерной, если её размерность равна единице. При этом [x]=[y₁]⁰[y₂]⁰…=1, x= . На этом основании говорят и о нулевой или единичной размерности. Все величины, не являющиеся безразмерными, называются размерными.

Примерами безразмерных величин являются относительные изменения любых величин 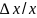, отношение дуги окружности к радиусу и т. д. Безразмерными являются переменные и постоянные, которыми оперирует «чистая» математика. С изменением размеров основных единиц числовое значение безразмерных величин не меняется.

Формула размерности любой физической величины однозначно определяется выбором основных единиц измерения и определяющего уравнения. Однако, одна и та же формула размерности можно соответствовать различным физическим величинам. Например, в СИ размерности работы, энергии, момент силы, количества теплоты совпадают и равны L²MT^-2.

Уравнение в виде степенного комплекса, не являющиеся определенными для единицы физической величины, может содержать в общем случае постоянный коэффициент k≠1,который может быть как безразмерной, так и размерной величиной. (Пример 1.4 и 1.5)

Число размерных коэффициентов (физических констант) в физических формулах зависит от числа основных единиц измерения. Чем больше это число, тем больше различных «универсальных» констант в физических формулах. Это затрудняет запоминание формул, удлиняет вычисления, усложняет установление эталонов основных единиц. Чем меньше число физических констант, тем проще физические формулы, но тем больше число единиц, обладающих одинаковыми размерностями.

Расчеты по математическим описаниям материальных объектов, т.е. по соответствующим физическим формулам и уравнениям, можно выполнять двояко. Если есть уверенность в размерной однородности всех членов и её соответствие определенной системе единиц измерения, то буквенные символы физических величин принимаются за числовые значения этих величин или данной системе единиц.

При отсутствии уверенности в размерной однородности членов буквенные символы принимаются за размеры величин. В этом случае числовой расчет сопровождаются анализом размерностей.