Лабораторна робота № 4

Тема: Методи багатомірної оптимізації 1-го та 2-го порядку. Методи спряжених градієнтів та Ньютону

Мета роботи: знайомство з методами багатомірної безумовної оптимізації другого порядку й близького до них по ефективності методу спряжених градієнтів, освоєння й порівняння ефективності їхнього застосування для конкретних цільових функцій.

1. Короткі теоретичні відомості

Розглядаються методи мінімізації:

1. метод Флетчеру-Рівса;

2. модифікація методу Флетчеру-Рівсу для мінімізації неквадратичної цільової функції.

3. метод Ньютону;

4. метод Ньютону-Рафсону із дробленням кроку;

5. метод Ньютону-Рафсону з оптимальним кроком;

6. модифікація I методу Ньютону;

7. модифікація II методу Ньютону.

Вступні зауваження

Матрицею Гесе подвійно диференційованої в точці x функції називається матриця часткових похідних другого порядку, обчислених в даній точці:

Якщо позначити , то отримаємо наступний запис:

Як видно, матриця є симетричною.

1.1 Метод спряжених градієнтів

1.1.1. Загальна характеристика методів спряжених градієнтів

Метод спряжених градієнтів відноситься до групи методів спряжених напрямків. Цей метод відноситься до методів першого порядку, тобто використовує інформацію тільки по першій похідній функції, що мінімізується. Однак метод спряжених градієнтів відрізняється від градієнтних методів більш високою швидкістю збіжності, що при певних припущеннях щодо цільової функції, наближається до швидкості збіжності методу Ньютону.

Два вектори x і y називають Н-спряженими (або спряженими стосовно матриці Н) або Н-ортогональними, якщо скалярний добуток

(x, H·y) = 0.

(1)

Спряженість можна вважати узагальненням поняття ортогональності. Справді, коли Н=Е, х та y відповідно до рівняння (1) ортогональні.

Розглянемо квадратичну функцію n змінних

.

(2)

з додатньо визначеною n×n матрицею. Виявляється, що квадратична функція (2) може бути мінімізованою методом спряжених напрямків не більш ніж за n кроків.

Щоб скористатися цим методом мінімізації квадратичної функції (2) потрібно знати n-взаємно спряжених напрямків S₀, S₁, …, S_n-1. Ефективність таких напрямків — самостійна проблема. Існує багато взаємно спряжених напрямків S₀, S₁, …, S_n-1 і способів їхньої побудови. Нижче викладається метод спряжених градієнтів Флетчера-Рівса, у якому вибір Н-спряжених напрямків здійснюється разом з одномірною мінімізацією f(х) по α.

1.1.2. Метод Флетчеру-Рівсу

Характеристика методу Флетчеру-Рівсу

Цей метод використовує послідовність напрямків пошуку, кожна з яких є лінійною комбінацією антиградієнта в поточній точці й попередньому напрямку спуску. Метод застосовується до квадратичної цільової функції

.

При мінімізації її методом Флетчеру-Рівсу вектори S_k обчислюються за формулами

,

.

Величини β_k-1 вибираються так, щоб напрямки S_k, S_k-1 були Н-спряженими.

Точка х_k-1 визначається в результаті мінімізації функції f(х) в напрямку S_k, що виходить із точки x_k, тобто

,

де α_k доставляє мінімум по α_k функції f(x_k, α ·S_k).

Отже, пропонована процедура мінімізації функції f(x) виглядає в такий спосіб. У заданій точці x₀ обчислюється антиградієнт S₀= –f '(x₀). Здійснюється одномірна мінімізація в цьому напрямку й визначається точка x₁. У точці x₁ знову обчислюється антиградієнт –f '(x₁). Оскільки ця точка доставляє мінімум функції f(x) уздовж напрямку S₀= –f'(x₀), вектор f '(x₁) ортогональний до f '(x₀). Потім за відомим значенням f '(x₁) по формулі (11) обчислюється вектор S₁, що за рахунок вибору β₀ буде Н-спряженим до S₀. Далі відшукується мінімум функції f(х) уздовж напрямку S₁ і т.д.

А лгоритм методу Флетчеру-Рівсу

Крок 1.

При k=0 задається початкове наближення x₀. Обчислення антиградієнта .

Крок 2.

Розв'язання задачі одномірної мінімізації по  функції f(x_k+·S_k), в результаті чого визначається величина кроку _k і точка x_k+1=x_k+_k·S_k.

Крок 3.

Обчислення величин f(x_k+1) і f '(x_k+1).

Крок 4.

Якщо , то x_k+1 — розв'язання задачі.

Інакше визначаємо новий напрямок пошуку: S_k+1 зі співвідношення :

.

Далі k=k+1 і перехід до кроку 2.

Це і є остаточний вид алгоритму Флетчера-Рівса. Як було помічено раніше, він знаходить мінімум квадратичної функції не більш ніж за n кроків.

1.1.3. Модифікація методу Флетчеру-Рівсу для мінімізаціі неквадратичної цільової функції

Метод Флетчера-Рівса може застосуються для мінімізації й неквадратичних функцій. Він є методом першого порядку й у той же час швидкість його збіжності квадратична. Зрозуміло, якщо цільова функція не квадратична, метод уже не буде кінцевим. Тому після (n+1)-й ітерації процедура повторюється із заміною x₀ на x_n+1, а рахунок закінчується при , де ε — задане число. При мінімізації неквадратичних функцій звичайно застосовується наступна модифікація методу Флетчеру-Рівсу.

С хема алгоритму для неквадратичних цільових функцій.

Крок 1.

При k=0 введення початкового наближення x₀ і умови зупинки ε_3. Обчислення антиградієнта S₀= –f '(x₀).

Крок 2.

Розв'язання задачі одномірної мінімізації по α функції f(x_k+·S_k), в результаті чого визначається величина кроку _k і точка x_k+1=x_k+_k·S_k.

Крок 3.

Обчислення величин f(x_k+1) і f '(x_k+1).

Крок 4.

Якщо , то точка x_k+1 — розв'язок задачі й на цьому пошук закінчується.

Інакше визначається коефіцієнт β_k по формулі:

Крок 5.

Обчислення S_k+1 по формулі .

Привласнюється k=k+1 і перехід до кроку 2.

Тут i — множина індексів, i={0, n, 2n, 3n, …}. Значення k, для яких β_k=0, називають моментами відновлення методу. Таким чином, відновлення методу відбувається через кожні n кроків.

1.2. Методи Ньютону

1.2.1. Загальна характеристика методів Ньютону

Методи Ньютону відносяться до методів другого порядку, тобто використовують другі частинні похідні цільової функції f(x). Всі вони є прямим узагальненням відомого методу Ньютону відшукання кореня рівняння:

φ(x)=0,

(3)

де φ(x) — скалярна функція скалярного аргументу x.

Метод Ньютону відшукання кореня рівняння описується наступною рекурентною формулою:

.

(4)

Цей метод ще називають методом дотичних для розв'язання рівняння (3).

Нехай тепер φ(x) — n-мірна вектор-функція векторного аргументу x тієї ж розмірності. Тоді для розв'язання системи рівнянь φ(x)=0 ми можемо використовувати ітераційний процес, аналогічний (4):

(5)

де  — квадратна матриця n×n.

Розглянемо тепер випадок, коли вектор-функція φ(x) є градієнтом деякої скалярної функції f(x), тобто

φ(x)=f '(x).

Прирівнюючи її до нуля, приходимо до системи рівнянь, яка визначає координати стаціонарних точок функції f(x). Формула методу Ньютону для розв'язання цієї системи виглядає так:

(6)

і отримується заміною в (6) φ(x_k) на f '(x).

Ітераційний процес (6) будує послідовність точок {x_k}, що при певних припущеннях сходиться до деякої стаціонарної точки x^ функції f(x), тобто до точки, у якій f '(x^)=0. Якщо матриця других похідних f ''(x^) позитивно визначена, ця точка буде точкою локального мінімуму функції f(x).

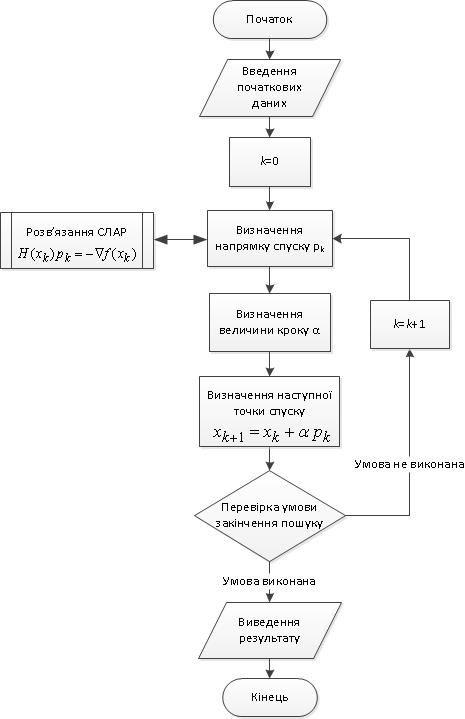
Рис. . Узагальнена схема оптимізаційних методів Ньютону