1.2. Метод обертових координат (метод Розенброка)

Ідея методу полягає в обертанні системи координат відповідно до зміни швидкості спадання цільової функції. Нові напрямки координатних осей визначаються таким чином, щоб одна з них відповідала напрямку найбільш швидкого спадання цільової функції, а інші знаходяться з умови ортогональності. Алгоритм методу полягає в наступному (рис. 7).

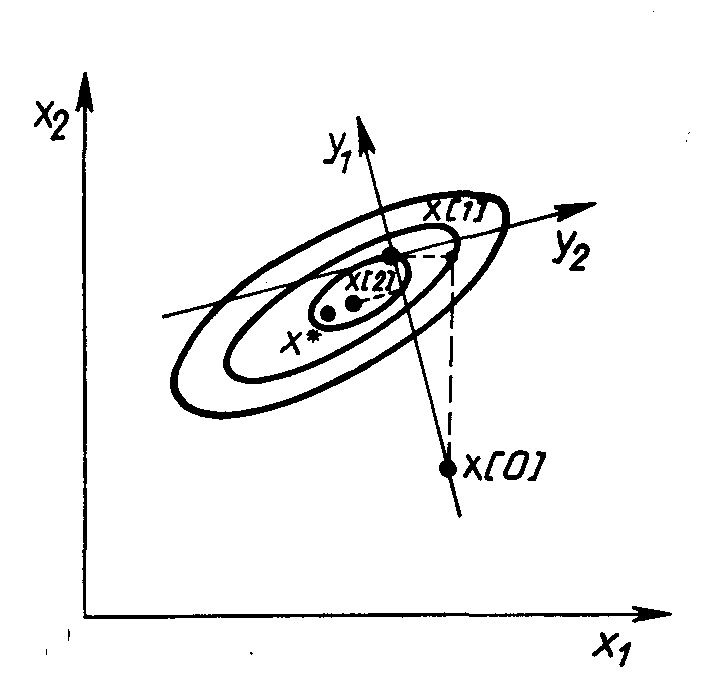
Рис. 

7. Геометрична інтерпретація методу Розенброка

З початкової точки х₀ здійснюють спуск у точку х₁ по напрямках, паралельним координатним осям. На наступній ітерації одна з осей повинна проходити в напрямку y₁=х₁–х₀, а інша — у напрямку, перпендикулярному до в₁. Спуск уздовж цих осей приводить у точку х₂, що дає можливість побудувати новий вектор х₂–х₁ і на його базі нову систему напрямків пошуку. У загальному випадку даний метод ефективний при мінімізації яружних функцій, тому що результуючий напрямок пошуку прагне розташуватися уздовж осі яру.

Алгоритм методу Розенброка

Крок 1

Позначають через напрямки координатних осей у деякій точці х_k (на к-й ітерації). Виконують пробний крок h₁ уздовж осі , тобто

.

Якщо при цьому , то крок h множать на величину >1;

Якщо , - то на величину (-), 0 < || < 1;

.

Приймаючи ?h₁=а₁.одержують

.

Крок 2

З точки виконують крок h₂ уздовж осі :

.

Повторюють операцію кроку 1, тобто

.

Цю процедуру виконують для всіх інших координатних осей. На останньому кроці одержують точку

.

Крок 3

Вибирають нові осі координат . В якості першої вісі приймається вектор

.

Інші вісі будують ортогональними до першої вісі за допомогою процедури ортогоналізації Грама-Шмідта. Повторюють обчислення з кроку 1 до виконання умов збіжності.

Коефіцієнти  підбираються емпірично. Гарні результати дають значення = –0,5 при невдалих пробах і =3 при вдалих пробах .

На відміну від інших методів нульового порядку алгоритм Розенброка орієнтований на відшукання оптимальної точки в кожному напрямку, а не просто на фіксоване зрушення в усіх напрямках. Величина кроку в процесі пошуку безупинно змінюється залежно від рельєфу поверхні рівня. Сполучення обертання координат з регулюванням кроку робить метод Розенброка ефективним при розв'язанні складних задач оптимізації.

1.3. Метод паралельних дотичних (метод Пауэлла)

Цей метод використовує властивість квадратичної функції, що полягає в тім, що будь-яка пряма, що проходить через точку мінімуму функції х*, перетинає під рівними кутами дотичні до поверхонь рівного рівня функції в точках перетинання (рис. 8).

Цей метод використовує властивість квадратичної функції, що полягає в тім, що будь-яка пряма, що проходить через точку мінімуму функції х*, перетинає під рівними кутами дотичні до поверхонь рівного рівня функції в точках перетинання (рис. 8).

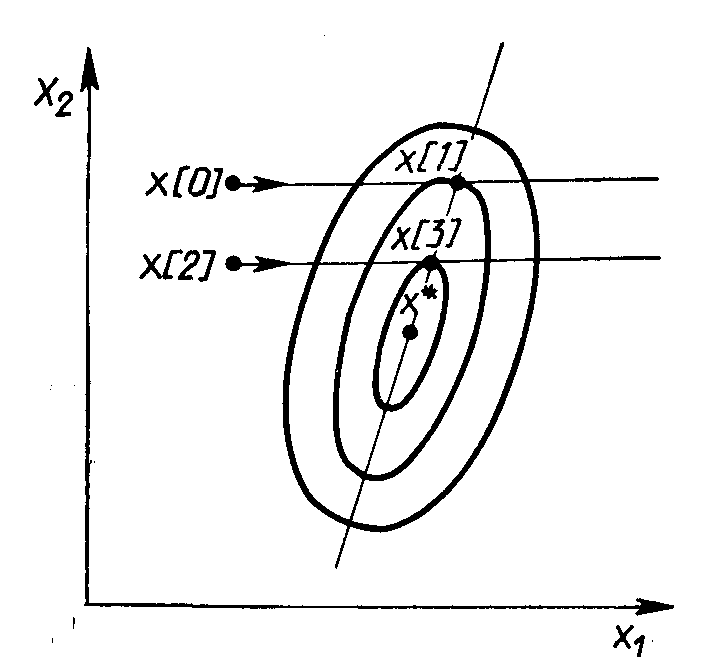
Рис. 

8. Геометрична інтерпретація методу Пауэлла

Суть методу така. Вибирається деяка початкова точка х₀ і виконується одномірний пошук уздовж довільного напрямку, що приводить у точку х₁. Потім вибирається точка х₂, що не лежить на прямій х₀–х₁, і здійснюється одномірний пошук уздовж прямій, паралельної х₀–х₁. Отримана в результаті точка х₃ разом з точкою х₁ визначає напрямок x₁–х₃ одномірні пошуки, що дає точку мінімуму х^*. У випадку квадратичної функції n змінних оптимальне значення знаходиться за п ітерацій. Пошук мінімуму при цьому в остаточному підсумку здійснюється у взаємно сполучених напрямках. У випадку неквадратичної цільової функції напрямки пошуку виявляються сполученими щодо матриці Гессе.

Алгоритм методу паралельних дотичних

Крок 1

Задається початкова точка x₀. За початкові напрямки пошуку р₁, …, р₀ приймають напрямки осей координат, тобто р_i=е_i, i=1, ..., n (тут e_i=(0, ..., 0, 1, 0, …, 0)^T).

Крок 2

Виконують n одномірних пошуків уздовж ортогональних напрямків р_i, i=1, ..., п. При цьому кожний наступний пошук виконується з точки мінімуму, отриманої на попередньому кроці. Величина кроку а_k знаходиться з умови

.

Отриманий крок визначає точку

.

Крок 3

Вибирають новий напрямок p=–x_n–х₀ і змінюють напрямки р₁, …, р_n на р₂, …, р_n, р. Останнім привласнюють позначення р[1],..., р[n].

Крок 4

Здійснюють одномірний пошук уздовж напрямку р=р_n=х_n–х₀. Заміняють х₀ на х_n+1=х_n+а_nр_п і приймають цю точку за початкову точку х₀ для наступної ітерації. Переходять до кроку 1.

Таким чином, у результаті виконання розглянутої процедури здійснюється почергова заміна прийнятих спочатку напрямків пошуку. У підсумку після n кроків вони виявляться взаємно сполученими.