Лабораторна робота № 3
Тема: Методи безумовної багатомірної оптимізації нульового порядку
Мета роботи: знайомство з методами багатомірної безумовної оптимізації нульового порядку, їхнє освоєння, порівняння ефективності застосування цих методів для конкретних цільових функцій.
1. Короткі теоретичні відомості
1.1. Методи прямого пошуку
1.1.1. Загальна характеристика методів прямого пошуку
Методи прямого пошуку — це методи, у яких використовуються тільки значення цільової функції (методи нульового порядку). Розглянемо наступні методи, засновані на евристичних міркуваннях. Ці методи досить часто застосовуються на практиці, дозволяючи в ряді випадків одержати задовільні розв'язання.
Основна перевага методів нульового порядку полягає в тому, що вони не вимагають безперервності цільової функції й існування похідних.
1.1.2. Метод конфігурацій (метод Хука й Дживса).
Ідея методу Хука-Дживса
Алгоритм містить у собі два основних етапи пошуку.
На початку досліджується окіл обраної точки (базисної точки), в результаті чого обирається прийнятний напрямок спуску.
У визначеному напрямку знаходиться точка з найменшим значенням цільової функції. Ця точка обирається в якості нової базисної точки.
Ця процедура триває доти, поки на околах базисних точок вдається знаходити прийнятні напрямки спуску.
Схема алгоритму методу Хука-Дживса
Крок 1.
Задаються:
—
початкове наближення (перша
базисна точка);
h — початковий крок для пошуку напрямку спуску;
— точність розв'язання (граничне значення для кроку h);
λ — множник прискорення.
Покласти к=0.
Крок 2. (Перший етап).
Визначається
напрямок мінімізації цільової функції
у базисній точці
.
Для цього послідовно дають приріст
змінним
у точці хк.
Покласти z=xk.
Циклічно давати приріст змінним xj і
якщо
f(z)<f(xk),
формуємо
,
якщо ж ні, то
якщо
f(z)<f(xk)
,
,
інакше z(j)=xk(j).
Так для всіх j(j=1,2,...,n).
Крок 3.
Якщо z=xk, тобто не визначився підходящий напрямок, то обстеження околиці базисної точки хк повторюється, але з меншим кроком h (наприклад, h=h/2).
Якщо h>, то перейти до кроку 2, тобто повторити обстеження точки хк.
Якщо h<, то пошук закінчується, тобто досягнуте граничне значення для кроку h і знайти прийнятний напрямок спуска не вдається. У цьому випадку покладається
Крок 4. (Другий етап).
Якщо zxk, то потрібно знайти нову базисну точку в напрямку вектора z–xk: xk+1=xk+(z–xk), де — коефіцієнт «прискорення пошуку».
Визначається таке значення =к, при якому досягається найменше значення цільової функції в обраному напрямку, тобто функції
f(xk +(z-xk) = ().
Залежно від способу вибору к можливі варіанти методу:
а) к==const постійного для всіх ітерацій;
б) задається початкове 0=, а далі к=к-1, якщо f(xk+1)<f(xk), інакше дробимо к, поки не виконається ця умова;
в) к визначається розв'язанням задачі одномірної мінімізації функції ().
У такий спосіб визначається нова базисна точка xk+1=xk + (z-xk). Приймаємо к=к+1 і пошук оптимального розв'язання повторюється із кроку 2.
1.1.3.Метод симплекса
Під симплексом розуміється n-мірний опуклий багатогранник n-мірного простору, що має n+1 вершину. Для n=2 це трикутник, а при n=3 це тетраедр.
Ідея методу полягає в порівнянні значень функції в n+1 вершинах симплекса й переміщенні симплекса в напрямку кращої точки. У розглянутому методі симплекс переміщається за допомогою операцій відбиття. Далі прийнятo наступне: х0(k), х1(k), …, хn(k) — вершини симплекса, де к — номер ітерації.
Рис.
1. Побудова нового симплекса
Схема алгоритму методу симплекса
Крок 1. Побудова початкового симплекса.
Для цього задаються початкова точка х0(0) і довжина ребра симплекса l. Формуються інші вершини симплекса: xi(0) = x0(0) + l*ei (i=1,2,…,n),де ei – одиничні вектори.
x2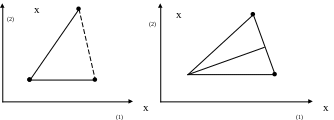
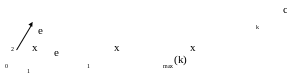
Рис.
2. Побудова початкового симплекса
Крок 2. Визначення напрямку поліпшення розв'язання.
Для цього на к-й ітерації обчислюються значення цільової функції в кожній точці симплекса. Нехай для всіх i:
,
де min, max, i — номера відповідних вершин симплекса. Визначимо центр ваги всіх точок, крім точки xmax(k),
.
Тоді напрямок поліпшення розв'язання визначається вектором
Ck–xmax(k).
Крок 3. Побудова відображеної точки.
Заміна вершини xmax(k) з максимальним значенням цільової функції на нову точку за допомогою операції відображення, результатом якої є нова точка:
Рис.