4. 7. Красно-черные деревья

Красно-чёрное дерево является особым видом двоичного дерева, используемым в компьютерной науке для организации сравнимых данных, таких как фрагменты текста или числа.

Листовые узлы красно-черных деревьев не содержат данных.

Такие листья не нуждаются в явном выделении памяти — нулевой указатель на потомка может фактически означать, что этот потомок — листовой узел, но в некоторых случаях работы с красно-черными деревьями использование явных листовых узлов может послужить упрощением алгоритма.

Другие названия: Red-black tree, RB tree.

Пример:

Давайте посмотрим, какой может быть максимальная глубина корректного красно-черного дерева с n вершинами.

Возьмем самый глубокий лист. Пусть он находится на глубине h. Из-за правила 1, как минимум половина вершин на пути из корня будет черными, то есть черная высота дерева будет не меньше h/2.

Можно показать, что в таком дереве будет не менее 2^(h/2)-1 черных вершин (так как у каждой черной вершины с черной глубиной k, если она не лист, должно быть как минимум два потомка с черной глубиной k+1).

Тогда 2^(h/2)-1 <= n или h <= 2*log2(n+1).

Все основные операции с красно-черным деревом можно реализовать за O(h), то есть O(log n) по доказанному выше.

Классическая реализация основана на разборе большого количества случаев и довольно трудна для восприятия.

Красно-черные деревья тесно связаны с B-деревьями.

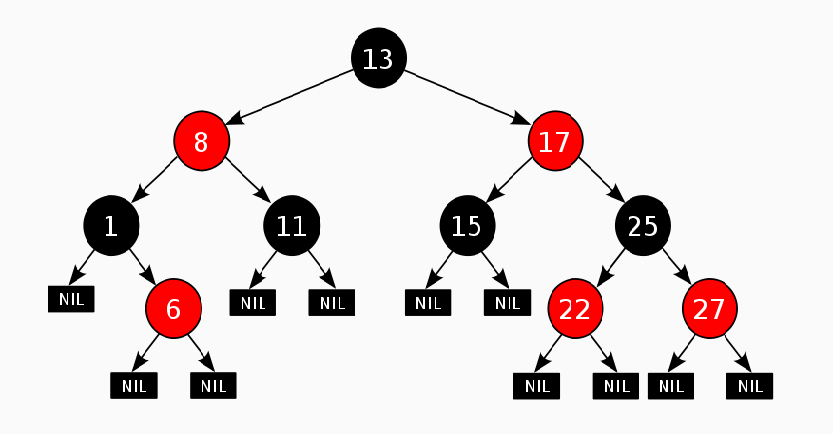
Свойства

Красно-чёрное дерево — двоичное дерево поиска, в котором каждый узел имеет атрибут цвет, принимающий значения красный или черный. В дополнение к обычным требованиям, налагаемым на двоичные деревья поиска, к красно-чёрным деревьям применяются следующие требования:

1. Узел либо красный, либо чёрный.

2. Корень — чёрный. (В других определениях это правило иногда опускается. Это правило слабо влияет на анализ, так как корень всегда может быть изменен с красного на чёрный, но не обязательно наоборот).

3. Все листья — черные.

4. Оба потомка каждого красного узла — черные.

5. Всякий простой путь от данного узла до любого листового узла, являющегося его потомком, содержит одинаковое число черных узлов.

Эти ограничения реализуют критическое свойство красно-черных деревьев:

путь от корня до самого дальнего листа не более чем в два раза длиннее пути от корня до ближайшего листа (если дальний лист расположен на 3-м уровне).

Результатом является то, что дерево примерно сбалансировано. Так как такие операции как вставка, удаление и поиск значений требуют в худшем случае времени, пропорционального длине дерева, эта теоретическая верхняя граница высоты позволяет красно-чёрным деревьям быть более эффективными в худшем случае, чем обычные двоичные деревья поиска.

4. 8. АВЛ-дерево. Сбалансированное дерево

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ — аббревиатура, образованная первыми буквами создателей (советских учёных) Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.

В АВЛ-дереве высоты h имеется не меньше F_h узлов, где F_h — число Фибоначчи.

Поскольку ,

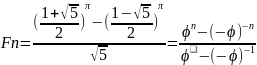где 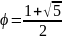— золотое сечение,

то имеем оценку на высоту АВЛ-дерева h=O(log(n)), где h — число узлов. Следует помнить, что h=O(log(n)) — мажоранта (функция), и её можно использовать только для оценки (Например, если в дереве только два узла, значит в дереве два уровня, хотя log(2)=1).

Балансировка АВЛ дерева

Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится <= 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.

Традиционно, узлы АВЛ-дерева хранят не высоту, а разницу высот правого и левого поддеревьев, которая может принимать только три значения -1, 0 и 1.

Для балансировки АВЛ-дерева используются 4 типа вращений:

1.Малое левое вращение

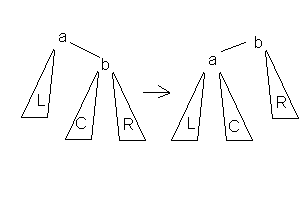
Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота С <= высота R.

2.Большое левое вращение

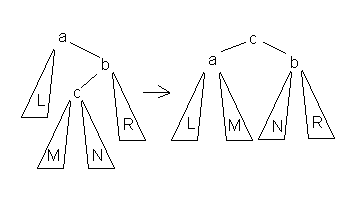
Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота c-поддерева > высота R.

3.Малое правое вращение

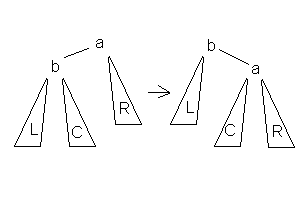
Данное вращение используется тогда, когда (высота b-поддерева — высота R) = 2 и высота С <= высота L.

4.Большое правое вращение

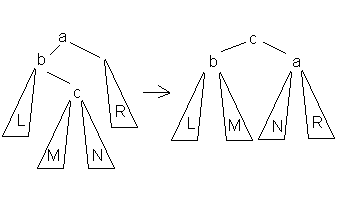
Данное вращение используется тогда, когда (высота b-поддерева - высота R) = 2 и высота c-поддерева > высота L.

Пример

Рассмотрим теперь ситуацию дисбаланса, когда высота правого поддерева узла p на 2 больше высоты левого поддерева (обратный случай является симметричным и реализуется аналогично).

Пусть q — правый дочерний узел узла p, а s — левый дочерний узел узла q.

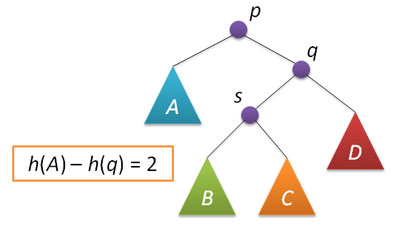
Анализ возможных случаев показывает, что для исправления расбалансировки в узле p достаточно выполнить либо простой поворот влево вокруг p, либо так называемый большой поворот влево вокруг того же p.

Простой поворот выполняется при условии, что высота левого поддерева узла q больше высоты его правого поддерева: h(s)≤h(D).

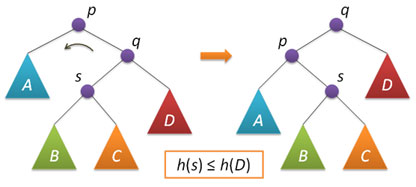
Большой поворот применяется при условии h(s)>h(D) и сводится в данном случае к двум простым — сначала правый поворот вокруг q и затем левый вокруг p.

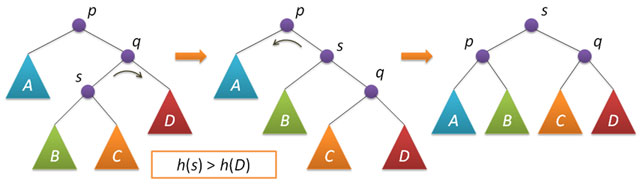
Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.