15.Уравнение сохранения массы при многофазной многокомпонентной фильтрации.

В основе рассмотрения лежит представление о пористой среде как о сплошной среде — фиктивном континууме, для каждой точки которого можно определить физические характеристики как непрерывные функции пространственных и временной координат. Значения физических переменных и параметров в точке пористой среды характеризуются представительными значениями для элементарного объема, содержащего эту точку. Элементарный объем должен быть достаточно большим по сравнению с размером пор и малым по сравнению с характерным масштабом пласта.

Уравнение сохранения массы (уравнение неразрывности) в декартовой системе координат

или, используя оператор дивергенции,

В цилиндрической системе координат (r,θ,z) уравнение (1.3) имеет вид:

(1.4)

ρ- плотность, u – скорость фильтрации, изменение массы компенсируется изменением за счет сжимаемости и за счет внешнего источника .

В случае многофазной многокомпонентной фильтрации уравнение неразрывности (1.3) можно обобщить следующим образом [22]. Пусть рассматриваемая система состоит из n_l фаз и n_c компонентов. Обычно количество фаз — не более трех: нефть, вода и газ. Как правило, вода - смачивающая фаза, газ – несмачивающая фаза, а нефть имеет промежуточную смачиваемость. В некоторых углеводородных системах между фазами происходит значительный массообмен отдельными химическими соединениями (компонентами). В этом случае сохранение баланса масс должно выполняться не только для каждой фазы, но и для каждого компонента. Количество компонентов может быть произвольным. Компоненты имеют различную концентрацию в различных фазах. При этом каждая фаза перемещается с различной скоростью.

Насыщенность 1-й фазой s_l определяется как доля порового пространства элементарного объема, занятая данной фазой. Пусть с_lj - массовая концентрация j-го компонента в l-й фазе. Тогда уравнение сохранения массы для j-го компонента имеет вид

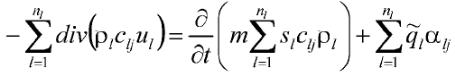(1.5)

З десь - интенсивность источника l-ой фазы, α_lj — массовая доля компонента j в 1-й фазе. Уравнение (1.5) учитывает только конвективный массоперенос, диффузионные процессы не учитываются.

В уравнениях (1.13) плотности и вязкости фаз являются известными функциями давления и компонентного состава. Относительные фазовые проницаемости также являются известными функциями насыщенностей. Значения и α_lj определяются в соответствии с граничными условиями. Таким образом, определению подлежат следующие неизвестные функции:

• массовые концентрации компонентов в каждой из фаз с_lj, давления в каждой из фаз p_l, насыщенности s_l.

16. Абсолютная проницаемость. Методы получения. Способ задания.

Проницаемость является наиболее изменчивым свойством коллектора, существенно влияющим на фильтрационные процессы и уровни добычи жидкости. Проницаемость определяется лабораторным путем по образцам породы, отобранным из пласта, либо по результатам гидродинамических исследований скважин. Если отсутствуют данные, полученные этими методами, пользуются регрессионным анализом и определяют проницаемость в зависимости от других известных параметров (например, пористости), причем коэффициенты уравнений регрессии находят по имеющейся информации для других областей пласта со сходными характеристиками.

Лабораторные измерения проницаемости основаны на измерении расхода Q жидкости или газа через образец пористой среды при заданном перепаде давления ΔР. Чтобы убедиться, что замеры производятся при ламинарном режиме фильтрации, можно задать несколько перепадов давления и построить график Q = Q(ΔР), который в этом случае является прямой линией, проходящей через начало координат. Искривление графика указывает на начало турбулентного режима. По наклону прямолинейного участка находят проницаемость k:

Здесь вязкость жидкости μ , площадь поперечного сечения S и длина L образца являются известными параметрами. При интерпретации результатов лабораторных измерений и их использовании при моделировании необходимо учитывать, что при извлечении керна из скважины на поверхность все силы, действующие на образец породы, снимаются, что ведет к его расширению и изменению геометрии поровых каналов. Уменьшение проницаемости в пластовых условиях под действием давления вышележащих пород может достигать в некоторых случаях 60%.

Размеры кернов определяются десятками сантиметров, поэтому для суждения о распределении проницаемости в межскважинном пространстве данных лабораторных измерений недостаточно. Наиболее достоверную информацию об эффективной проницаемости пласта на масштабах, сопоставимых с расстояниями между скважинами, можно получить по результатам гидродинамических исследований скважин и гидропрослушивания (пьезометрии). В этом случае для определения параметров пласта решается обратная задача, и проницаемость определяется по данным поведения давления на упругом режиме фильтрации.